MATLAB小波变换工具箱 Wavelet Toolbox 实际操作与训练

这篇本章是对MATLAB 中小波变换工具箱运用的一个简单总结，对结果进行了简单的阐述。原理部分涉及的较少，偏重应用，主要参考了董长虹主编的《MATLAB小波分析工具箱原理与应用》 ，主要针对一维信号。

1. 前言

传统的傅里叶分析中，信号是完全在频域展开，不包含任何时域信息。而小波变换具有多分辨率的特点，在时域和频域上都有表征局部信息的能力，时间窗和频率窗都可以根据信号的具体形态动态调整，在低频部分采用较低的时间分辨率，提高频率的分辨率，在高频情况下，采用较低的频率分辨率来获得精确的时间定位。
小波变换被广泛地应用在诸多领域，在信号分析方面主要用于滤波、去噪、压缩和传递等方面。

2. 小波变换的基本数学原理

2.1小波函数

如果函数能在有限的区域内迅速衰减到0，这样的函数具有紧支集。这样的函数可以被称为母小波，由它生成的一组正交基称为小波函数。
定义如下：如果$\Psi (t)\in L^2(R)$满足容许性条件：
$C_{\Psi }={\int }_{-\infty }^{\infty }\frac{|\hat{\Psi }(\omega ){|}^2}{|\omega |}d\omega <\infty$
那么$\Psi (t)$叫做可允许小波（积分小波，基小波），其中$\hat{\Psi }(\omega )$是$\Psi (t)$的傅里叶变换。
由基小波生成的小波函数系可以表示为：
${\Psi }_{a,b}(t)=|{a|}^{-1/2}\Psi \left(\frac{t-b}{a}\right)$

2.2 连续小波变换

定义：设$f(t)\in L^2(R)$，则对其的连续小波变换为：
$\left(W_{\Psi }f\right)(a,b)={\int }_{-\infty }^{\infty }f(t)\overline{{\Psi }_{a,b}(t)}\mathrm{d}t$

2.3 离散小波变换

离散小波函数可以表示为：
${\Psi }_{j,k}(t)=a_0^{-j/2}\Psi \left(a_0^{-j}t-k{b}_0\right),j,k\in Z$
离散小波变换的系数可以表示为：
$W_{j,k}(t)={\int }_{-x}^{\infty }f(t)\overline{{\Psi }_{j,k}(t)}\mathrm{d}t$
离散小波变换的重构公式为：
$f(t)=C{\sum }_{-\infty }^{\infty }{\sum }_{-\infty }^{\infty }{W}_{j,k}{\Psi }_{j,k}(t)$
其中C为与信号无关的常数，如果取a0=2，b0=1，则称为二进小波变换

2.4 正交小波变换

设${\left\{{\Psi }_{j,n}(x)\right\}}_{j,n\in Z}$是$L^2(R)$的标准化正交基，由于对于$\forall f\in L^2(R)$，都有
$f(x)={\sum }_{j,n\in Z}<f,{\Psi }_{j,n}>{\Psi }_{j,n}(x)$

2.5 小波函数介绍

• Haar小波，支集长度1，滤波器长度2
  ${\Psi }_H=\{\begin{array}{l}1,0⩽x⩽\frac{1}{2}\\ -1,\frac{1}{2}⩽x⩽1\\ 0\end{array}$
• Daubechies小波，db1小波等同于Haar小波，其余小波没有解析的表达式
  db小波的支集长度和滤波器长度都是2N左右

3. 小波变换在MATLAB中的实现

3.1 小波变换

使用Matlab进行1维小波分析主要使用的函数有：

• wavedec小波分解
• waverec 小波重建
• appcoef 近似系数
• detcoef 细节系数
  
  下面直接用具体的例子来进行说明：

clc;clear
load sumsin
figure
plot(sumsin)
title('Signal')
figure
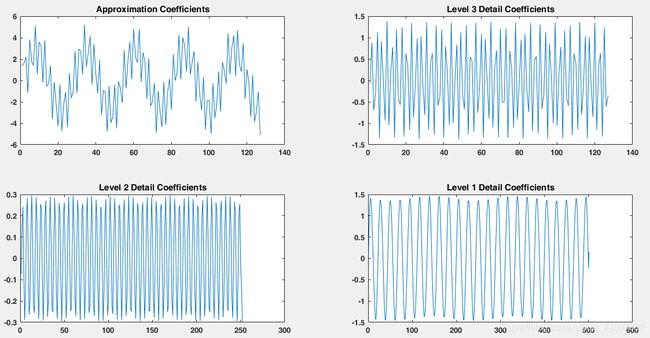
[c,l]=wavedec(sumsin,3,'db2');
approx=appcoef(c,l,'db2');
[cd1,cd2,cd3]=detcoef(c,l,[1,2,3]);
subplot(2,2,1)
plot(approx)
title('Approximation Coefficients')
subplot(2,2,2)
plot(cd3)
title('Level 3 Detail Coefficients')
subplot(2,2,3)
plot(cd2)
title('Level 2 Detail Coefficients')
subplot(2,2,4)
plot(cd1)
title('Level 1 Detail Coefficients')
x=waverec(c,l,'db2');
figure
plot(x)

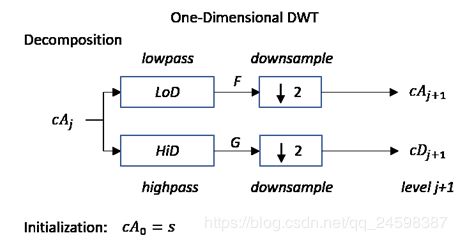
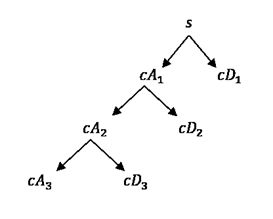
从小波变换的算法中其实可以看到，MATLAB中小波变换的算法实际上是先不断的将信号通过高通和低通滤波器后，进行2倍下采样的过程，因此信号会越来越短。
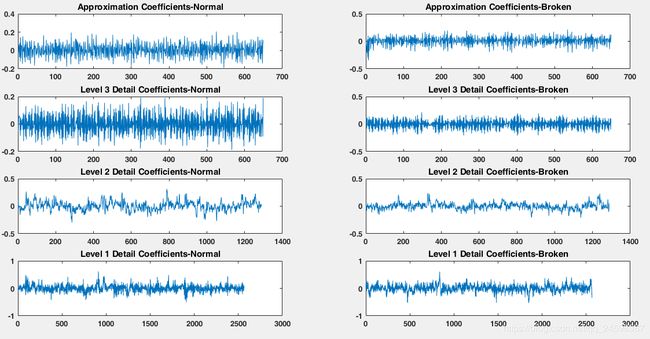
接下来对具体信号进行实验：

clear;clc;
%电机数据均为15Hz，内部负载为80load，采样率为5120Hz，取1个周期的数据
%由于频率过高，进行降采样，频率为1280Hz，采样点为1280
load('normal.mat');
normal=data(1:4:5120*4,5);
load('broken.mat');
broken=data(1:4:5120*4,5);
figure;
plot(normal,'r')
hold on 
plot(broken,'b')
hold off 
title('Sigal')
legend('normal','broken')
figure;
[c1,l1]=wavedec(normal,3,'db6');
approx=appcoef(c1,l1,'db6');
[cd1,cd2,cd3]=detcoef(c1,l1,[1,2,3]);
subplot(4,2,1)
plot(approx)
title('Approximation Coefficients-Normal')
subplot(4,2,3)
plot(cd3)
title('Level 3 Detail Coefficients-Normal')
subplot(4,2,5)
plot(cd2)
title('Level 2 Detail Coefficients-Normal')
subplot(4,2,7)
plot(cd1)
title('Level 1 Detail Coefficients-Normal')
[c2,l2]=wavedec(broken,3,'db6');
approx=appcoef(c2,l2,'db6');
[cd1,cd2,cd3]=detcoef(c2,l2,[1,2,3]);
subplot(4,2,2)
plot(approx)
title('Approximation Coefficients-Broken')
subplot(4,2,4)
plot(cd3)
title('Level 3 Detail Coefficients-Broken')
subplot(4,2,6)
plot(cd2)
title('Level 2 Detail Coefficients-Broken')
subplot(4,2,8)
plot(cd1)
title('Level 1 Detail Coefficients-Broken')

3.2小波包变换

小波包变换的主要函数有：

• wpdec：1维小波 包分解
• wprec：1维小波包重建
• wpcoef：小波包系数
• wprcoef：小波包系数重建
• bestttree:最好小波树分析
  wpdec的基本用法是：
  T=wpdec(s,N,‘wavename’)
  同样使用具体函数进行说明：

clc;clear;
load leleccum;s=leleccum;
wpt=wpdec(s,3,'db6');
figure;
plot(wpt)
figure;
c22=wpcoef(wpt,[2 2]);%等价于cww=wpcoef(wpt,5);
plot(c22)

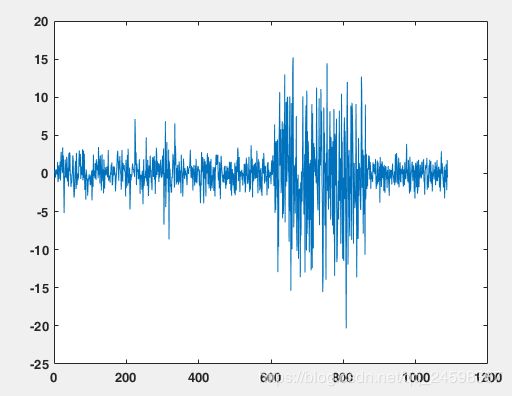而重建小波系数信息的命令wprcoef和wpcoef有所布偶听，wpcoef只是根据子节点的信息重建小波包系数，重建的长度只有1/2^j，而wprcoef则是根据本节点的子节点和同层的其他节点的信息重建小波包系数。可以得到原信号的完全信息，重建一个和原始信号长度一致的小波包系数。
由于小波包分解使一个树型结构，进行小波包变换的基本思想是让信息能量集中，在细节系数中寻找有序性，因此单纯把所有系数进行分解没有实际的帮助，只会增加计算量，因此需要有一定的衡量原则，一般采用熵最小原则，熵越小，信息的规律性越强，一般的判别方法是看系数分解后的系数的熵的和是否大于原系数的熵。在小波包分解的过程中还可以设置不同的熵计算方法。