朴素贝叶斯算法（2）案例实现

• 朴素贝叶斯算法（1）超详细的算法介绍
• 朴素贝叶斯算法（2）案例实现
• github代码地址

引言

关于朴素贝叶斯算法的推导过程在朴素贝叶斯算法（1）超详细的算法介绍中详细说明了，这一篇文章用几个案例来深入了解下贝叶斯算法在三个模型中（高斯模型、多项式模型、伯努利模型）的运用。

案例一：多项式模型

特征属性$X_i$是症状和职业，类别$Y=C_k$是疾病（包括感冒，过敏、脑震荡）
某个医院早上收了六个门诊病人，如下表：

症状	职业	疾病
打喷嚏	护士	感冒
打喷嚏	农夫	过敏
头痛	建筑工人	脑震荡
头痛	建筑工人	感冒
打喷嚏	教师	感冒
头痛	教师	脑震荡

现在又来了第七个病人，是一个打喷嚏的建筑工人。请问他患上感冒的概率有多大？

根据贝叶斯定理：$P(Y|X)=P(X|Y)P(Y)/P(X)$
字符定义：
$Y=C_k(k=1,2,3)$ ：其中k表示三种疾病（感冒、过敏、脑震荡）
$X=X_i(i=1,2)$：i表示特征属性（症状、职业）
$X_i=X_{1j}(j=1,2)$：j表示特征属性症状的取值（打喷嚏、头痛）
$X_2=X_{2j}(j=1,2,3,4)$：j表示特征属性职业的取值（护士、农夫、建筑工人、教师）
$m:样本总数$
$m_k:类别为k的样本数$
$m_{ij}:特征X_i各个类别的取值数$
$m_{kij}:类别为k,特征X_i各个类别的样本个数$

未做拉普拉斯平滑的效果展示：
$$\begin{gathered} P(感冒|打喷嚏\ast 建筑工人) \\ =P(Y=C_1|X_1=X_{11},X_2=X_{23}) \\ =\frac{P(X_1=X_{11},X_2=X_{23}|Y=C_k)P(Y=C_1)}{P(X_1=X_{11},X_2=X_{23})} \\ =\frac{P(X_1=X_{11}|Y=C_1)P(X_2=X_{23}|Y=C_1)P(Y=C_1)}{P(X_1=X_{11})P(X_2=X_{23})} \\ =\frac{m_{111}/m_1\ast m_{123}/m_1\ast m_1/m}{m_{11}/m\ast m_{23}/m}=>\frac{2/3\ast 1/3\ast 3/6}{3/6\ast 2/6}=\frac{2}{3} \end{gathered}$$

经过拉普拉斯平滑的效果展示：

$$\begin{gathered} P(感冒|打喷嚏\ast 建筑工人) \\ =P(Y=C_1|X_1=X_{11},X_2=X_{23}) \\ =\frac{P(X_1=X_{11},X_2=X_{23}|Y=C_k)P(Y=C_1)}{P(X_1=X_{11},X_2=X_{23})} \\ =\frac{P(X_1=X_{11}|Y=C_1)P(X_2=X_{23}|Y=C_1)P(Y=C_1)}{P(X_1=X_{11})P(X_2=X_{23})} \\ =\frac{(m_{111}+1)/(m_1+o_1)\ast (m_{123}+1)/(m_1+o_2)\ast m_1/m}{m_{11}/m\ast m_{23}/m}=>\frac{3/5\ast 2/7\ast 3/6}{3/6\ast 2/6}=\frac{18}{35} \end{gathered}$$
$$\frac{(m_{111}+1)/(m_1+o_1)\ast (m_{123}+1)/(m_1+o_2)\ast (m_1+1)/(m+o)}{(m_{11}+1)/(m+o_1)\ast (m_{23}+1)/(m+o_2)}=>\frac{3/5\ast 2/7\ast 4/9}{4/8\ast 3/10}=\frac{32}{63}$$

代码实现思路：

1. 构建训练集trainDataSet()
2. 获得四个信息 info()
   $m:样本总数$
   $m_k:类别为k的样本数$
   $m_{ij}:特征X_i各个类别的取值数$
   $m_{kij}:类别为k,特征X_i各个类别的样本个数$
3. 根据输入特征，计算概率calculate_probability()

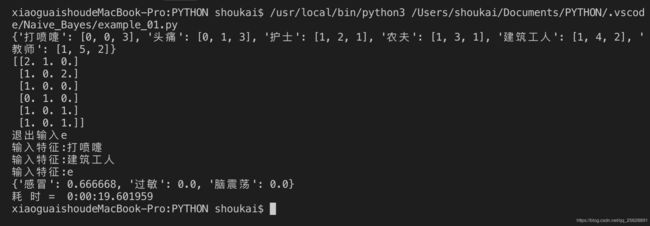
附上代码1：未经过平滑

import pandas as pd
import numpy as np
import collections
import datetime

# Bayes算法主体: 计算测试样本对应各个类别的概率
def bayes(feature, m, m_k, m_index, m_fk):
    """
    得到测试样本的分类概率

    Parameters
    ----------
        feature: numpy.array
        m: int
        m_k: dict
        m_index: dict
        m_fk: numpy.array
        
    Returns
    -------
        result: numpy.array
    """
    chance = {}
    for (key, value) in m_k.items():
        ll = len(feature)
        prob = 1.0
        for i in range(ll):
            t1 = m_index[feature[i]]
            t2 = m_fk[t1[1]]
            prob = round(prob*t2[value[0]]/t1[2], 6)
            if i==ll-1:
                prob = round(prob * m**(ll-1) / value[1]**(ll-1), 6)
                chance[key] = prob

    print(chance)
    return  chance

# 构建训练集数据向量，以及对应分类标签
def trainDataSet():
    """
    构建训练集数据，从.cvs文件中读取数据，最后一列为标签label，前面为训练集数据的特征feature
    """
    csv_data = np.array(pd.read_csv('./data/trainimg/bayes/example_01.csv'))
    train_label = csv_data[:,2]
    attr_count = len(csv_data[0])
    train_data = csv_data[:,0:attr_count-1]

    return train_data, train_label


def info(train_data, train_label):
    """
    返回四个值:
        样本总数m
        类别为k的字典表m_k
        特征X_i各个类别的取值数m_index
        类别为k,特征X_i各个类别的样本个数的表m_fk

    Parameters
    ----------
        train_data: numpy.array
        train_label: numpy.array

    Returns
    -------
        m, m_k, m_index, m_fk
    """
    # 样本总数m
    m = len(train_data)

    # 建立类别为k的字典表，key=(1,2...k)，value为[类别k的实际名字,类别为k的样本数]
    m_k = {}
    k = 0
    label_counter = collections.Counter(train_label)
    for (key,value) in label_counter.items():
        m_k[key] = [k, value]
        k += 1
    
    # 用一个字典表存储特征X_i各个类别的取值数, m_index{key: [i:特征i, sum:m_fk对应编号, value:该类别的取值数]}
    m_index = {}
    sum = 0
    for i in range(len(train_data[0])):
        data_counter = collections.Counter(train_data[:,i])
        for (key,value) in data_counter.items():
            m_index[key]=[i, sum, value]
            sum += 1
    print(m_index)

    # 创建一个二维数组m_fk存储m_ijk信息
    m_fk = np.zeros((len(m_index), len(m_k)))
    i = 0
    for (key,value) in m_index.items():
        m_ij = np.where(train_data[:,value[0]] == key,1,0)
        for j in range(len(m_ij)):
            if m_ij[j]==1:
                # 查找疾病对应标签
                k = m_k[train_label[j]][0]
                m_fk[i][k] += 1
        i += 1
    print(m_fk)
    return m, m_k, m_index, m_fk


def main():
    # 计时开始
    t1 = datetime.datetime.now()

    train_data,train_label = trainDataSet()
    m, m_k, m_index, m_fk = info(train_data, train_label)
    feature = []
    print('退出输入e')
    while True:
        try:
            ss = input('输入特征:')
            if ss == 'e':
                break
            feature.append(ss)
        except ValueError:
            print('输入有误, 请重新输入!')
    
    probability = bayes(feature, m, m_k, m_index, m_fk)

    t2 = datetime.datetime.now()
    print('耗 时 = ', t2 - t1)

if __name__ == "__main__":
    main()

附上代码2：经过平滑

import pandas as pd
import numpy as np
import collections
import datetime

# Bayes算法主体: 计算测试样本对应各个类别的概率
def bayes(feature, m, m_k, m_index, m_fk):
    """
    得到测试样本的分类概率

    Parameters
    ----------
        feature: numpy.array
        m: int
        m_k: dict
        m_index: dict
        m_fk: numpy.array
        
    Returns
    -------
        result: numpy.array
    """
    chance = {}
    for (key, value) in m_k.items():
        ll = len(feature)
        prob = 1.0
        for i in range(ll):
            t1 = m_index[feature[i]]
            t2 = m_fk[t1[1]]
            prob = round(prob * (t2[value[0]]+1)/(value[1]+t1[3])/t1[2]*m, 10)
            print(t2[value[0]]+1, '/', value[1]+t1[3], '/', t1[2], '*', m, '*', end='')
            # prob = round(prob * (t2[value[0]]+1)/(value[1]+t1[3])/(t1[2]+1)*(m+t1[3]), 10)
            # print(t2[value[0]]+1, '/', value[1]+t1[3], '/', t1[2]+1, '*', m+t1[3], '*', end='')
            if i==ll-1:
                prob = round(prob * value[1]/m, 10)
                print(value[1], '/', m)
                # prob = round(prob * (value[1]+1)/(m+len(m_k)), 10)
                # print(value[1]+1, '/', m+len(m_k))
                print()
                chance[key] = prob

    print(chance)
    return  chance

# 构建训练集数据向量，以及对应分类标签
def trainDataSet():
    """
    构建训练集数据，从.cvs文件中读取数据，最后一列为标签label，前面为训练集数据的特征feature
    """
    csv_data = np.array(pd.read_csv('./data/trainimg/bayes/example_01.csv'))
    train_label = csv_data[:,2]
    attr_count = len(csv_data[0])
    train_data = csv_data[:,0:attr_count-1]

    return train_data, train_label


def info(train_data, train_label):
    """
    返回四个值:
        样本总数m
        类别为k的字典表m_k
        特征X_i各个类别的取值数m_index
        类别为k,特征X_i各个类别的样本个数的表m_fk

    Parameters
    ----------
        train_data: numpy.array
        train_label: numpy.array

    Returns
    -------
        m, m_k, m_index, m_fk
    """
    # 样本总数m
    m = len(train_data)

    # 建立类别为k的字典表，key=(1,2...k)，value为[类别k的实际名字,类别为k的样本数]
    m_k = {}
    k = 0
    label_counter = collections.Counter(train_label)
    for (key,value) in label_counter.items():
        m_k[key] = [k, value]
        k += 1
    
    # 用一个字典表存储特征X_i各个类别的取值数, m_index{key: [i:特征i, sum:m_fk对应编号, value:该类别的取值数, len_i:特征i的个数]}
    m_index = {}
    sum = 0
    for i in range(len(train_data[0])):
        data_counter = collections.Counter(train_data[:,i])
        len_i = len(data_counter)
        for (key,value) in data_counter.items():
            m_index[key]=[i, sum, value, len_i]
            sum += 1
    print(m_index)

    # 创建一个二维数组m_fk存储m_ijk信息
    m_fk = np.zeros((len(m_index), len(m_k)))
    i = 0
    for (key,value) in m_index.items():
        m_ij = np.where(train_data[:,value[0]] == key,1,0)
        for j in range(len(m_ij)):
            if m_ij[j]==1:
                # 查找疾病对应标签
                k = m_k[train_label[j]][0]
                m_fk[i][k] += 1
        i += 1
    # print(m_fk)
    return m, m_k, m_index, m_fk


def main():
    # 计时开始
    t1 = datetime.datetime.now()

    train_data,train_label = trainDataSet()
    m, m_k, m_index, m_fk = info(train_data, train_label)
    feature = []
    print('退出输入e')
    while True:
        try:
            ss = input('输入特征:')
            if ss == 'e':
                break
            feature.append(ss)
        except ValueError:
            print('输入有误, 请重新输入!')
    
    probability = bayes(feature, m, m_k, m_index, m_fk)

    t2 = datetime.datetime.now()
    print('耗 时 = ', t2 - t1)

if __name__ == "__main__":
    main()