【深度学习】过拟合抑制(二)丢弃法(dropout)
概述
前一篇文章【深度学习】过拟合抑制(一)权重衰减(weight decay)中,简要介绍了利用权重衰减进行过拟合拟制,在深度模型中还常用丢弃法应对过拟合问题。丢弃法有许多变体,这里的丢弃法为倒置丢弃法(inverted dropout)。
本文为《动手学深度学习》一书学习笔记,原书地址:http://zh.d2l.ai/chapter_deep-learning-basics/dropout.html
原理
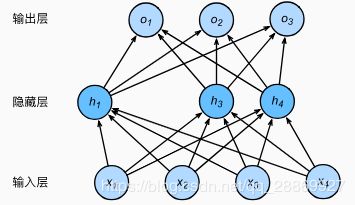
如【深度学习】多层感知机(二)MXNet实现双层感知机一文中提到的单隐藏层感知机(如下图所示),其输入层节点数为4,隐藏层节点数为5,故而隐藏层节点 h i ( i = 1 , 2 , 3 , 4 , 5 ) h_i(i=1, 2, 3, 4, 5) hi(i=1,2,3,4,5)的输出值计算方法为:
h i = ϕ ( x 1 w 1 i + x 1 w 1 i + x 2 w 2 i + x 3 w 3 i + x 4 w 4 i + b i ) h_i=\phi(x_1w_{1i}+x_1w_{1i}+x_2w_{2i}+x_3w_{3i}+x_4w_{4i}+b_i) hi=ϕ(x1w1i+x1w1i+x2w2i+x3w3i+x4w4i+bi)
其中 ϕ \phi ϕ表示激活函数, b i b_i bi表示偏差, w j i ( j = 1 , 2 , 3 , 4 ) w_{ji}(j=1, 2, 3, 4) wji(j=1,2,3,4)表示第 i i i个隐藏层节点和输入层连接之间的权重。

当我们对隐藏层使用丢弃法时,这一层的节点有一定的概率被丢弃,即其输出值被置0. 我们假设丢弃的概率为 p p p,那么 h i h_i hi将有 p p p的概率被置0,有 1 − p 1-p 1−p的概率会除以 1 − p 1-p 1−p做拉升。这里的丢弃概率就是丢弃法中的超参数。那么为什么可以对隐藏层进行这样的操作呢?
假设随机变量 ξ \xi ξ的分布列如下,显然我们可以知道 ξ \xi ξ的期望 E ( ξ ) = 1 − p E(\xi)=1-p E(ξ)=1−p。
| ξ \xi ξ | 0 0 0 | 1 1 1 |
|---|---|---|
| P | p | 1-p |
当我们使用丢弃法重新计算隐藏层节点 h i h_i hi时, h i ′ = ξ 1 − p h i h_i^{'}=\frac{\xi}{1-p}h_i hi′=1−pξhi,则 E ( h i ′ ) = E ( ξ ) 1 − p h i = h i E(h_i^{'})=\frac{E(\xi)}{1-p}h_i=h_i E(hi′)=1−pE(ξ)hi=hi,即使用丢弃法不改变隐藏层节点的期望。
我们对上述单隐藏层感知机使用丢弃法时,一种情况如下图所示:其中 h 2 h_2 h2和 h 5 h_5 h5被清0了,这时网络的输出值将不再依赖于 h 2 h_2 h2和 h 5 h_5 h5。反向传播是,与这两个节点相关的权重都为0。值得注意的是,在训练的过程中,隐藏层的任何节点都有可能被丢弃,下图描述的只是一种可能的情况。由于训练时节点丢弃的随机性,所以训练过程中输出层的计算结果无法过度依赖于隐藏层中的某个或者某几个节点,从而在训练模型的时候起到了正则化的作用,可以用于应对过拟合。在测试过程中,为了取得确定性的结果,不使用丢弃法。
实验
丢弃方法
我们如何对一个数组中的元素按照一定的概率丢弃(置0)呢?可以借助于均匀分布。
# coding=utf-8
# author: BebDong
# 2019/1/15
from mxnet import nd
# X表示使用丢弃法的矩阵,drop_prop为丢弃概率
def dropout(X, drop_prob=0):
# 首先检查drop_prob值是否处于正确范围
assert 0 <= drop_prob <= 1
# 如果丢弃概率为1,则全部置0
if drop_prob == 1:
return X.zeros_like()
# 借助均匀分布生成X的掩码
keep_prob = 1 - drop_prob # 保留(拉升)概率
mask = nd.random.uniform(0, 1, X.shape) < keep_prob
# 做拉升
return mask * X / keep_prob
# 丢弃概率
drop_prob = 0.2
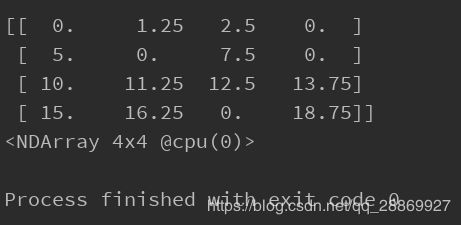
# 生成一个测试矩阵
X = nd.arange(16).reshape(4, 4)
print(dropout(X, drop_prob))
Fashion-MNIST数据集实验
这里我们通过MXNET深度学习框架在Fashion-MNIST数据集进行一个丢弃法的实验。如果对其中MXNET的用法不了解,可以参考:
- MXNET官方API文档
- 《动手学深度学习》
- 【深度学习】MXNet基本数据结构NDArray常用操作
- 【深度学习】MXNet自动求解函数梯度
- 【深度学习】Fashion-MNIST数据集简介
- 以及笔者前面其他关于MXNET实现机器学习模型的文章
实验代码如下:
# coding=utf-8
# author: BebDong
# 2019/1/14
# 丢弃法:定义两个隐藏层的感知机,使用Fashion-MNIST数据集进行测试
from mxnet import autograd, gluon, init
from mxnet.gluon import loss as gloss, nn, data as gdata
# 超参数
data_batch_size = 256 # 数据批量大小
hidden1_num = 300 # 隐藏层节点个数
hidden2_num = 200
drop_prop1 = 0.1 # 隐藏层丢弃概率,建议靠近输入层的丢弃概率小一点
drop_prop2 = 0.2
lr = 0.1 # 学习率
epochs = 10 # 训练次数
# 分批读取数据并做数据预处理
transformer = gdata.vision.transforms.ToTensor()
mnist_train = gdata.vision.FashionMNIST(train=True)
mnist_test = gdata.vision.FashionMNIST(train=False)
train_iter = gdata.DataLoader(mnist_train.transform_first(transformer), data_batch_size, shuffle=True)
test_iter = gdata.DataLoader(mnist_test.transform_first(transformer), data_batch_size, shuffle=False)
# 定义模型
net = nn.Sequential()
loss = gloss.SoftmaxCrossEntropyLoss()
net.add(nn.Dense(hidden1_num, activation="relu"), # 第一隐藏层及其丢弃层
nn.Dropout(drop_prop1),
nn.Dense(hidden2_num, activation="relu"), # 第二隐藏层及其丢弃层
nn.Dropout(drop_prop2),
nn.Dense(10)) # 输出层
# 初始化模型参数
net.initialize(init.Normal(sigma=0.01))
# 丢弃法训练模型
trainer = gluon.Trainer(net.collect_params(), 'sgd', {'learning_rate': lr})
for epoch in range(epochs):
# 每个epoch的损失和准确率
train_l_sum, train_acc_sum = 0.0, 0.0
for X, y in train_iter:
with autograd.record():
y_hat = net(X)
los = loss(y_hat, y)
los.backward()
trainer.step(data_batch_size)
# 每个epoch损失 = epoch内每个小批次中每个样本的平均损失之和
train_l_sum += los.mean().asscalar()
# 准确率计算:理解Fashion-MNIST数据集和交叉熵损失函数,从而理解模型输出和标记(label)的关系
train_acc_sum += (y_hat.argmax(axis=1) == y.astype('float32')).mean().asscalar()
print('epoch %d, loss %.4f, train acc %.3f' % (
epoch + 1, train_l_sum / len(train_iter), train_acc_sum / len(train_iter)))
# 计算测试准确率
acc = 0
for X, y in test_iter:
acc += (net(X).argmax(axis=1) == y.astype('float32')).mean().asscalar()
test_acc = acc / len(test_iter)
print("testing accuracy: ", test_acc)
设置丢弃概率均为0时(drop_prob1 = 0, drop_prob2 = 0),即不使用丢弃法,得到结果:
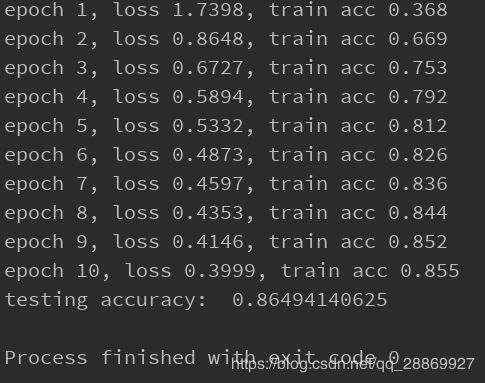
使用丢弃法,设置drop_prob1 = 0.1, drop_prob2 = 0.2,可以得到结果:
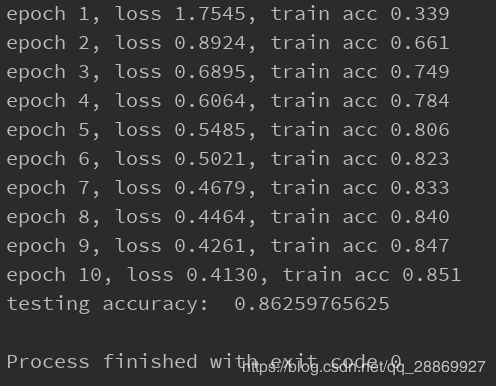
由于这个实验中本身未出现过拟合现象,所以使用丢弃法和不使用丢弃法的结果一致,如果有兴趣的同学可以参照笔者博客【深度学习】过拟合抑制(一)权重衰减(weight decay)中,设置合适的场景,使得过拟合现象明显,再使用丢弃法观察前后的结果差别。
另外,对比【深度学习】Softmax回归(三)MXNet深度学习框架实现一文中利用Softmax回归跑Fashion-MNIST数据集的结果可以看到,本实验中使用的三层感知机(双隐藏层)可以取得更好的效果。