GhostNet: More Features from Cheap Operations

GhostNet: More Features from Cheap Operations

论文地址：https://arxiv.org/abs/1911.11907

---

Ghost Module

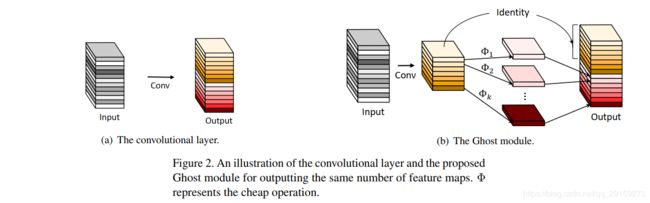
设输入为 $X\in {\mathbb{R}}^{c\times h\times w}$，其中$c$是输入通道数，$h$和$w$分别是高和宽。卷积层可表述为：
$$Y=X\ast f+b$$其中，$\ast$是卷积操作，$b$是偏置项，$Y\in {\mathbb{R}}^{h^{\prime }\times w^{\prime }\times n}$是输出的$n$维feature map，$f\in {\mathbb{R}}^{c\times k\times k\times n}$是卷积核。
这个卷积过程中，FLOPs可以用$n\cdot h^{\prime }\cdot w^{\prime }\cdot c\cdot k\cdot k$来计算。这个数字往往非常巨大。然而，生成的feature map具有冗余性，因此，如果要得到相同的feature map，完全可以通过卷积生成一部分intrinsic feature map，另一部分通过对intrinsic feature map进行cheap transform得到。这样就可以缩减运算量。

利用
$$Y=X\ast f$$生成了$m$个通道的intrinsic feature map $Y^{\prime }\in {\mathbb{R}}^{h^{\prime }\times w^{\prime }\times m}$，$m\le n$，偏置项为了简化而略去了。

为了得到$n$个通道的feature map，对intrinsic feature map进行一系列线性运算：
$$y_{ij}={\varphi }_{i,j}\left(y_i^{\prime }\right),\forall i=1,\cdots ,m,j=1,\cdots ,s$$其中，$y_i^{\prime }$是intrinsic feature map中的第$i$个map，${\varphi }_{i,j}$是$y_i^{\prime }$生成第$j$个ghost feature map的线性运算，也就是说，每个$y_i^{\prime }$可以生成$s$个ghost feature map ${\left\{y_{ij}\right\}}_{j=1}^s$；而${\varphi }_{i,s}$是恒等映射，将intrinsic feature map保留至最终输出的feature map中。

由此得到了$n=m\cdot s$ 维的feature map $Y=\left[y_{11},y_{12},\cdots ,y_{ms}\right]$，作为Ghost module的输出。

与现有方法的不同

1. 现有方法（MobileNet、SqueezeNetShuffleNet等）广泛使用$1\times 1$点卷积；而Ghost module可以自定义卷积核大小
2. 现有方法大都是先用pointwise卷积降维、再用depthwise卷积进行特征提取；而Ghost module则是先做原始卷积获得 intrinsic feature map，再用简单的线性变换来获取更多feature map
3. 现有方法中处理每个特征图大都使用depthwise卷积或shift操作；而Ghost module使用线性变换，可以有很大的多样性
4. Ghost module中利用恒等映射与线性变换来保留intrinsic feature map

复杂度分析

由于有1次恒等映射，因此有$m\cdot \left(s-1\right)=\frac{n}{s}\cdot \left(s-1\right)$次线性运算，每个线性运算核大小平均为$d\times d$。加速比可以计算为：

$$\begin{gathered} r_s=\frac{n\cdot h^{\prime }\cdot w^{\prime }\cdot c\cdot k\cdot k}{\frac{n}{s}\cdot h^{\prime }\cdot w^{\prime }\cdot c\cdot k\cdot k+\left(s-1\right)\cdot \frac{n}{s}\cdot h^{\prime }\cdot w^{\prime }\cdot d\cdot d} \\ =\frac{c\cdot k\cdot k}{\frac{1}{s}\cdot c\cdot k\cdot k+\frac{s-1}{s}\cdot d\cdot d}\approx \frac{s\cdot c}{s+c-1}\approx s \end{gathered}$$其中，$d\times d$和$k\times k$的量级相似，而$s\ll c$。

类似地，压缩比可以计算为：
$$r_c=\frac{n\cdot c\cdot k\cdot k}{\frac{n}{s}\cdot c\cdot k\cdot k+\frac{s-1}{s}\cdot d\cdot d}\approx \frac{s\cdot c}{s+c-1}\approx s$$

---

Ghost bottlenect (G-bneck)

如图，Ghost bottleneck和ResNet中的residual block相似：

• G-bneck中包含2个Ghost module。第一个充当了expansion layer，用于扩张通道数；第二个则缩减通道数，以此和shortcut path相匹配。
• 每一层都使用了batch normalization
• 每层的激活函数都是ReLU（除了第二个Ghost module之后的层不用【具体原因参考MobileNetV2】）
• $stride=2$时，shortcut path通过降采样层实现，而两个Ghost module之间还添加了一个$stride=2$的深度卷积层
• 实践中，为了提高效率，Ghost module中所有“基础卷积”都是点卷积

---

GhostNet

将MobileNetV3中的bottleneck block替换成G-bneck，搭建了GhostNet：

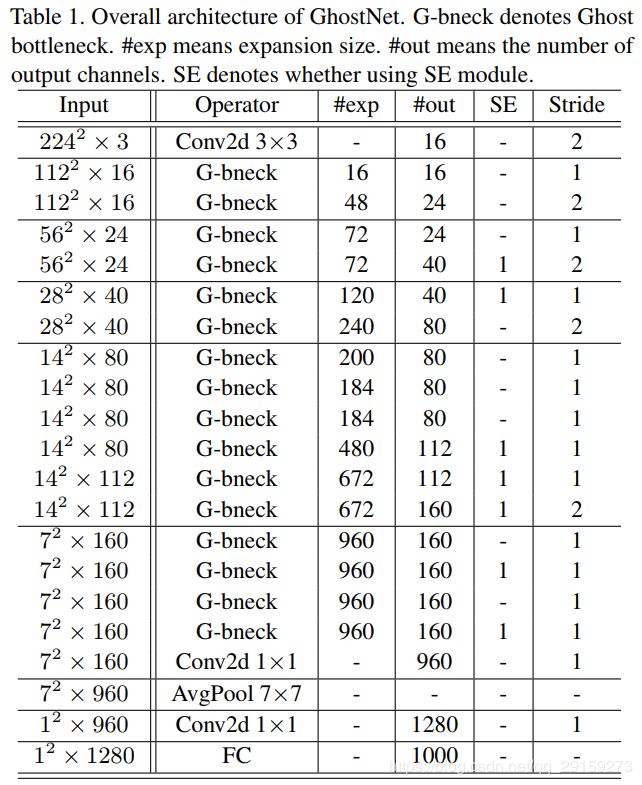
• 第1层是标准的卷积层，卷积核有16个
• 根据G-bneck的输入feature map大小，将网络分为若干组
• 每组最后一个G-bneck的 $stride=2$，其余 $stride=1$
• 最终使用global average pooling，并通过卷积层，将feature map映射为1280维的feature vector，用于分类问题
• 某些G-bneck中使用了squeeze and excite (SE) module
• 和MoileNetV3不同，没有使用hard-swish，因为其时延过大

---

实验

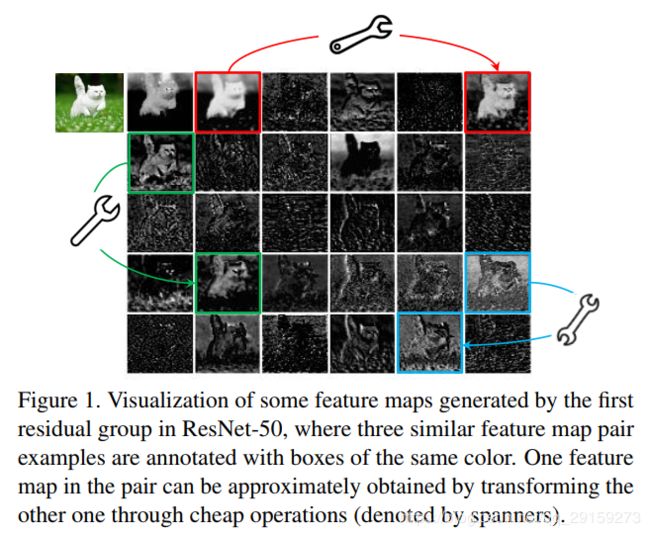
首先进行一个验证性实验，观察原始feature map和生成的ghost feature map之间的重构误差。

以图1中的3对feature map为例，ResNet50第一个残差块提取出的特征，把左边的作为输入，右边的作为输出，用深度卷积学习映射关系（这是一个线性的关系），深度卷积大小为$d$，$d$取不同值时，MSE值为：

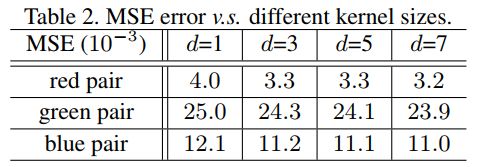
由表可知，MSE值很小，也就是说，feature map之间确实存在着很强的关联性，feature map存在着冗余性。

---

参考资料：

CVPR2020 | GhostNet：超越MobileNetV3！使用简单的线性变换生成特征图的轻量级网络