吴恩达机器学习笔记(一)之梯度下降和线性回归
文章目录
- Machine Learning
- 一、介绍
- 1.1 机器学习的概念
- 1.2 分类
- 1.2.1 监督学习
- 1.2.2 无监督学习(Unsupervised Learning)
- 2 Model and Cost Function
- 2.1 模型表示
- 2.2 代价函数(Cost Function)
- 2.2.1 代价函数的直观理解1
- 2.2.2 代价函数的直观理解2
- 2.3 梯度下降(Gradient descent)
- 2.3.1 概念
- 2.3.2 梯度下降的直观理解
- 2.3.3 梯度下降的线性回归
- 参考文献:
Machine Learning
一、介绍
1.1 机器学习的概念
汤姆·米切尔(Tom Mitchell)提供了一个定义:“如果某计算机程序在T任务上的性能(由P来衡量)随着经验E的提高而提高,则可以说它是从经验E中学习有关某类任务T和性能指标P的。 ”
1.2 分类
1.2.1 监督学习
- 回归(Regression)问题:目标是推测一个连续的值的输出(具体的数值:比如说房价)
- 分类(Classification)问题:目标是推测离散值输出(比如说肿瘤的类型,0代表良性1代表恶性)
Question:假设你经营着一家公司,你想开发学习算法来处理这两个问题:
-
你有一大批同样的货物,想象一下,你有上千件一模一样的货物等待出售,这时你想预测接下来的三个月能卖多少件?
-
你有许多客户,这时你想写一个软件来检验每一个用户的账户。对于每一个账户,你要判断它们是否曾经被盗过?
那这两个问题,它们属于分类问题、还是回归问题?
问题一是一个回归问题,因为你知道,如果我有数千件货物,我会把它看成一个实数,一个连续的值。因此卖出的物品数,也是一个连续的值。
问题二是一个分类问题,因为我会把预测的值,用 0 来表示账户未被盗,用 1 表示账户曾经被盗过。所以我们根据账号是否被盗过,把它们定为0 或 1,然后用算法推测一个账号是 0 还是 1,所以它归为分类问题。
总结:监督学习问题分为“回归”和“分类”。在回归问题中,我们试图预测连续输出中的结果;在分类问题中,我们尝试预测离散输出中的结果。
1.2.2 无监督学习(Unsupervised Learning)
有一堆数据。我不知道数据里面有什么。我不知道谁是什么类型。我甚至不知道人们有哪些不同的类型,这些类型又是什么。但你能自动地找到数据中的结构吗?就是说你要自动地聚类那些个体到各个类,我没法提前知道哪些是哪些。因为我们没有给算法正确答案来回应数据集中的数据,所以这就是无监督学习。
无监督学习使我们几乎或根本不了解结果应该是什么样子。我们可以从数据中获得结构,而不必知道变量的影响。我们可以通过基于数据中变量之间的关系对数据进行聚类来推导此结构。在无监督学习的情况下,没有基于预测结果的反馈。
例:
聚类:收集1,000,000个不同的基因,然后找到一种方法,将这些基因自动分组为通过不同变量(例如寿命,位置,角色等)在某种程度上相似或相关的组。
非聚类:“Cocktail Party Algorithm”,使您可以在混乱的环境中找到结构。(即在Cocktail party上从一连串的声音中识别出个人声音和音乐)。
2 Model and Cost Function
2.1 模型表示
以之前的预测房价问题为例,假使我们回归问题的训练集(Training Set)如下表所示:

我们将要用来描述这个回归问题的标记如下:
m 代表训练集中实例的数量
x 代表特征/输入变量
y 代表目标变量/输出变量
(x,y) 代表一个训练样本
( x ( i ) , y ( i ) ) ({{x}^{(i)}},{{y}^{(i)}}) (x(i),y(i)) 代表第 i i i 个训练样本
h h h 代表学习算法的解决方案或函数也称为假设(hypothesis)
这就是一个监督学习算法的工作方式,我们可以看到这里有我们的训练集里房屋价格
解决房价预测问题,我们实际上是要将训练集“喂”给我们的学习算法,进而学习得到一个假设 h h h,然后将我们要预测的房屋的尺寸作为输入变量输入给 h h h,预测出该房屋的交易价格作为输出变量输出为结果。那么,对于我们的房价预测问题,我们该如何表达 h h h?
h h h 代表hypothesis(假设),输入是房屋尺寸大小, y y y 值对应房子的价格 因此, h h h 是一个从 x x x 到 y y y 的函数映射。
一种可能的表达方式为: h θ ( x ) = θ 0 + θ 1 x h_\theta \left( x \right)=\theta_{0} + \theta_{1}x hθ(x)=θ0+θ1x,因为只含有一个特征/输入变量,因此这样的问题叫作单变量线性回归问题。
2.2 代价函数(Cost Function)
我在线性回归中我们有一个像这样的训练集, m m m代表了训练样本的数量,比如 m = 47 m = 47 m=47。而我们的假设函数,也就是用来进行预测的函数,是这样的线性函数形式: h θ ( x ) = θ 0 + θ 1 x h_\theta \left( x \right)=\theta_{0}+\theta_{1}x hθ(x)=θ0+θ1x。
接下来我们会引入一些术语为我们的模型选择合适的参数(parameters) θ 0 \theta_{0} θ0 和 θ 1 \theta_{1} θ1,在房价问题这个例子中便是直线的斜率和在 y y y 轴上的截距。
我们选择的参数决定了我们得到的直线相对于我们的训练集的准确程度,模型所预测的值与训练集中实际值之间的差距(下图中蓝线所指)就是建模误差(modeling error)

我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数。 即使得代价函数 J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J \left( \theta_0, \theta_1 \right) = \frac{1}{2m}\sum\limits_{i=1}^m \left( h_{\theta}(x^{(i)})-y^{(i)} \right)^{2} J(θ0,θ1)=2m1i=1∑m(hθ(x(i))−y(i))2最小。
2.2.1 代价函数的直观理解1
先看个简单地例子,假设其中一个参数 θ 0 = 0 \theta_{0} = 0 θ0=0
如果我们尝试从视觉上考虑它,我们的训练数据集将分散在x-y平面上。我们正在尝试画一条直线(定义为 h θ ( x ) h_\theta \left( x \right) hθ(x))穿过这些分散的数据点。
我们的目标是获得最佳的生产线。最佳可能的线应是这样,以使散射点与该线的平均垂直垂直距离最小。理想情况下,直线应穿过训练数据集的所有点。在这种情况下, J ( θ 0 , θ 1 ) J(\theta_{0}, \theta_{1}) J(θ0,θ1)将为0。以下示例显示了成本函数为0的理想况。
此时 θ 1 = 1 \theta_{1}= 1 θ1=1, h θ ( x ) h_\theta \left( x \right) hθ(x)贯穿模型中的每个数据点。相反,当 θ 1 = 0.5 \theta_{1}= 0.5 θ1=0.5 。如下图所示,我们看到从拟合到数据点的垂直距离增加了。
这将我们的成本函数提高到0.58。绘制其他几个点可得出下图:
因此,作为目标,我们应尽量减少代价函数。在这种情况下, θ 1 = 1 \theta_{1} =1 θ1=1时,代价函数最低。
2.2.2 代价函数的直观理解2
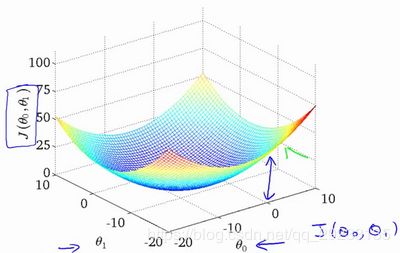
这是代价函数 J ( θ 0 , θ 1 ) J(\theta_{0}, \theta_{1}) J(θ0,θ1)的3D曲面图
可以用等高线图来表示3D曲面图,取任何颜色并沿“圆”走,代价函数都有相同的值。例如,在下面的绿线上找到的三个绿点具有相同 J ( θ 0 , θ 1 ) J(\theta_{0}, \theta_{1}) J(θ0,θ1)的值。带圆圈的x在出现以下情况时在,左侧显示图形的代价函数的值 θ 0 = 800 \theta_{0}=800 θ0=800和 θ 1 = − 0.15 \theta_{1}=-0.15 θ1=−0.15,假设函数 h θ ( x ) h_\theta \left( x \right) hθ(x)的图像如下图所示。
当 θ 0 = 360 \theta_{0}=360 θ0=360和 θ 1 = 0 \theta_{1}=0 θ1=0时,代价函数 J ( θ 0 , θ 1 ) J(\theta_{0}, \theta_{1}) J(θ0,θ1)的值在等高线图中更靠近中心,从而减少了误差。
现在给我们的假设函数一个稍微为正的斜率,就可以更好地拟合数据。当$ \theta_{0}=250 和 和 和 \theta_{1}=$0.12时,代价函数更小了。
2.3 梯度下降(Gradient descent)
2.3.1 概念
梯度下降是一个用来求函数最小值的算法,我们将使用梯度下降算法来求出代价函数 J ( θ 0 , θ 1 ) J(\theta_{0}, \theta_{1}) J(θ0,θ1) 的最小值。
梯度下降背后的思想是:开始时我们随机选择一个参数的组合 ( θ 0 , θ 1 , . . . . . . , θ n ) \left( {\theta_{0}},{\theta_{1}},......,{\theta_{n}} \right) (θ0,θ1,......,θn),计算代价函数,然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到找到一个局部最小值(local minimum),因为我们并没有尝试完所有的参数组合,所以不能确定我们得到的局部最小值是否便是全局最小值(global minimum),选择不同的初始参数组合,可能会找到不同的局部最小值
梯度下降的算法为:
其中 a a a是学习率(learning rate),它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大,在批量梯度下降中,我们每一次都同时让所有的参数减去学习速率乘以代价函数的导数。
在每次迭代 j j j 时.同时更新 θ 0 {\theta_{0}} θ0和 θ 1 {\theta_{1}} θ1,下图左边为正确的更新方式。
2.3.2 梯度下降的直观理解
首先使用一个参数 θ 1 \theta_{1} θ1的情况,并绘制其代价函数以实现梯度下降。我们的单个参数公式为:
θ 1 : = θ 1 − α d d θ 1 J ( θ 1 ) {\theta_{1}}:={\theta_{1}}-\alpha \frac{\ d}{\ d {\theta_{1}}}J\left( \theta_{1} \right) θ1:=θ1−α dθ1 dJ(θ1)
J ( θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J \left( \theta_1 \right) = \frac{1}{2m}\sum\limits_{i=1}^m \left( h_{\theta}(x^{(i)})-y^{(i)} \right)^{2} J(θ1)=2m1i=1∑m(hθ(x(i))−y(i))2
下图所示,(这点的导数就是这点的斜率),当斜率为负时, θ 1 {\theta_{1}} θ1更新后等于 θ 1 {\theta_{1}} θ1减去一个正数数乘以 a a a, θ 1 {\theta_{1}} θ1是减小的,当斜率为正时; θ 1 {\theta_{1}} θ1增大。
那么 a a a学习率要时刻调整吗?
在梯度下降法中,当我们接近局部最低点时,梯度下降法会自动采取更小的幅度,这是因为当我们接近局部最低点时,很显然在局部最低时导数等于零,所以当我们接近局部最低时,导数值会动变得越来越小,所以梯度下降将自动采取较小的幅度,这就是梯度下降的做法。所以实际上没有必要再另外减小 a a a。
2.3.3 梯度下降的线性回归
梯度下降是很常用的算法,它不仅被用在线性回归上和线性回归模型、平方误差代价函数。接下来将梯度下降和代价函数结合。我们将用到此算法,并将其应用于具体的拟合直线的线性回归算法里。
梯度下降算法和线性回归算法比较如图:
对我们之前的线性回归问题运用梯度下降法,关键在于求出代价函数的导数,即:
∂ ∂ θ j J ( θ 0 , θ 1 ) = ∂ ∂ θ j 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 \frac{\partial }{\partial {{\theta }_{j}}}J({{\theta }_{0}},{{\theta }_{1}})=\frac{\partial }{\partial {{\theta }_{j}}}\frac{1}{2m}{{\sum\limits_{i=1}^{m}{\left( {{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}} \right)}}^{2}} ∂θj∂J(θ0,θ1)=∂θj∂2m1i=1∑m(hθ(x(i))−y(i))2
j = 0 j=0 j=0 时: ∂ ∂ θ 0 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) \frac{\partial }{\partial {{\theta }_{0}}}J({{\theta }_{0}},{{\theta }_{1}})=\frac{1}{m}{{\sum\limits_{i=1}^{m}{\left( {{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}} \right)}}} ∂θ0∂J(θ0,θ1)=m1i=1∑m(hθ(x(i))−y(i))
j = 1 j=1 j=1 时: ∂ ∂ θ 1 J ( θ 0 , θ 1 ) = 1 m ∑ i = 1 m ( ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x ( i ) ) \frac{\partial }{\partial {{\theta }_{1}}}J({{\theta }_{0}},{{\theta }_{1}})=\frac{1}{m}\sum\limits_{i=1}^{m}{\left( \left( {{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}} \right)\cdot {{x}^{(i)}} \right)} ∂θ1∂J(θ0,θ1)=m1i=1∑m((hθ(x(i))−y(i))⋅x(i))
则算法改写成:
Repeat {
θ 0 : = θ 0 − a 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) {\theta_{0}}:={\theta_{0}}-a\frac{1}{m}\sum\limits_{i=1}^{m}{ \left({{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}} \right)} θ0:=θ0−am1i=1∑m(hθ(x(i))−y(i))
θ 1 : = θ 1 − a 1 m ∑ i = 1 m ( ( h θ ( x ( i ) ) − y ( i ) ) ⋅ x ( i ) ) {\theta_{1}}:={\theta_{1}}-a\frac{1}{m}\sum\limits_{i=1}^{m}{\left( \left({{h}_{\theta }}({{x}^{(i)}})-{{y}^{(i)}} \right)\cdot {{x}^{(i)}} \right)} θ1:=θ1−am1i=1∑m((hθ(x(i))−y(i))⋅x(i))
}
但是我们在此处为线性回归提出的优化问题只有一个全局最优,而没有其他局部最优。因此,梯度下降总是会收敛(假设学习率α不太大)到全局最小值。实际上, J ( θ 0 , θ 1 ) J(\theta_{0}, \theta_{1}) J(θ0,θ1)是一个凸二次函数。
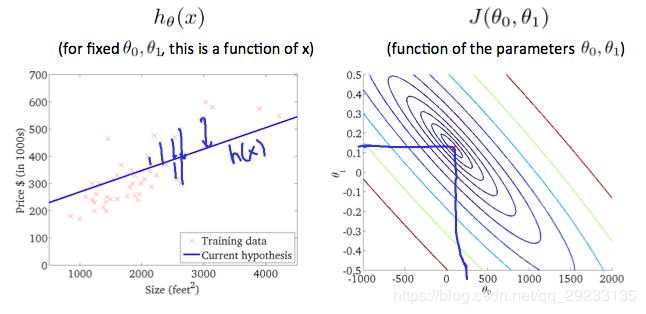
下图显示了梯度下降所采取的轨迹,该轨迹在(48,30)处初始化。图中的x(由直线连接)标记了梯度下降收敛到最小值时经历的θ的连续值。也成为“Batch” Gradient Descent(批量梯度下降),因为每一次更新参数都遍历了整个数据集。
参考文献:
https://github.com/fengdu78/Coursera-ML-AndrewNg-Notes
https://www.coursera.org/course/ml