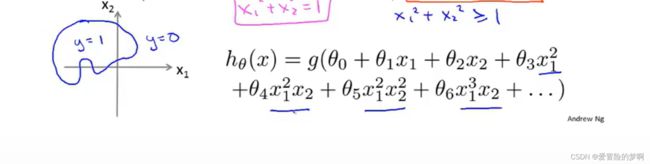【吴恩达机器学习笔记详解】第六章 逻辑回归
第五章主要讲的是编程语言的介绍,因为我们现在用python的比较多,所以就没有再看那一章。但是5.6值得看一下
5.6 矢量
现在的变成语言包含了各种各样的矩阵库,所以通常进行矩阵计算的时候我们直接用命令即可,如果使用了合适的向量化方法,代码会简单很多。
下面进行一些例子的讲解。
这是线性回归的假设函数,他是从0到j的一个求和,我们也可以把他看作是矩阵的相乘,θ的转置×x,可以写成计算两个向量的内积。
前面的如果要是用代码实现的话,就要用到for循环,因为从0到j,后面的用代码的话直接用矩阵相乘即可。
这是梯度下降的公式,我们用向量化来进行表示。

这里把看作θ是n+1维的向量,α是个实数,δ也是n+1维的向量,所以梯度更新实际上是一个向量的减法运算。其中粉红色的预测的减去实际的值是个实数,Xi是个向量,这样里面的加和就可以像u=3v+5w的形式去表示,也就是向量的加法。

最后,如果你在实施线性回归的时候,使用两个以上的特征量,有时我们在线性回归中使用几十甚至上百个特征,当使用向量化 实现线性回归时,相比于for循环速度更快。
6.1 分类
从这节开始,我们讨论预测的变量y是一个离散的值的时候下的分类问题。

这里的分类问题不像是我们之前讨论的预测房价啊,从0到10000等等,这里的分类是要么是0,要么是1.

如图所示,我们用线性回归进行数据的拟合的时候,可能一开始还比较实用,但是当出现另一个点的时候,这时候我们要调整线性回归的曲线,来调整曲线拟合,这样正确率不高并且不方便。所以讲线性回归应用到分类问题是不合适的。
对于假设函数输出可能是大于1或者小于0的,但是我们目标的标签是0或者1,所以我们就引入了逻辑回归(Logistic Regression)他利用sigmoid函数可以讲输出压缩在0-1之间。

6.2 假设陈述
逻辑回归就是用了下图所示的sigmoid函数,将输出压缩到0-1之间

下面是对假设输出的解释,当假设输出输出一个数字的时候,我们会将这个数字当作对一个输入x,y等于1的概率估计。
我觉得可以理解为h(x)是当输入为x的时候,输出y等于1的概率有多大
下面是个例子来解释。x特征和之前一样,一个是1,一个是肿瘤的大小,将他的特征喂给我的假设中,并且假设我的假设输出是0.7,这个假设告诉我们对于一个特征为x的患者,y=1的概率是0.7,也就是百分之70的概率这个肿瘤是恶性的。我们用数学的式子来表示,下面这个图中的式子表述在给定X的条件下y=1的概率,即病人的特征为x的情况下,也就是代表着肿瘤的大小,这个概率的参数为θ(条件概率)

6.3 决策边界
这个假设函数输出给定x和参数θ的时候,y=1的估计概率。
我们设定假设函数大于等于0.5的时候就把y归为正类,也就是y=1
函数小于0.5的时候,我们把y归为负类,也就是y=0.
我们通过sigmoid函数也可以看出来,当我们想要g(z)大于等于0.5的时候,也就是预测y=1的时候,要保证z是大于0的,同理g(z)小于0.5的时候,z要小于0的。
以此例子为例,我们想要预测y=1,就要使得-3+x1+x2大于等于0,移位也就等于x1+x2大于等于3,我们把这条直线代表的平面表示出来,也就是图中的上半部分。只要在上办部分的点,我们都会把它预测为y=1,下半部分的点我们会把它预测为y=0. 这条直线就叫做决策边界
决策边界是假设函数的一个属性,在这里它包括参数θ,θ1,θ2,这条决策边界取决于它的参数,而不是取决于数据集

对于这个例子,圈和❌代表的是不同的类型,而这里的决策边界是非线性的,那我们如何拟合这些数据呢?我们之前讲过多项式回归或线性回归的时候,我们谈到可以在特征中添加额外的高阶多项式,我们也可以对逻辑回归使用相同的方法,这里我们已经在假设函数中添加了两个额外的特征x1的平方和x2的平方,所以现在我们有五个参数,下节课我们会讲如何选择参数的值来拟合数据,假设这个先知道了,我们每个参数都知道,如图所示,那么参数θ向量是这样,这样再转换到,如果我们预测y=1的话,那么要求-1+x1的平方+x2的平方应该大于等于0的,这其实是根据参数θ的向量写出来的,这样决策边界就出来了,是半径为1的圆。
6.4 代价函数
这一节我们讲如何拟合逻辑回归模型的参数θ,用来拟合参数的优化目标或者叫做代价函数。
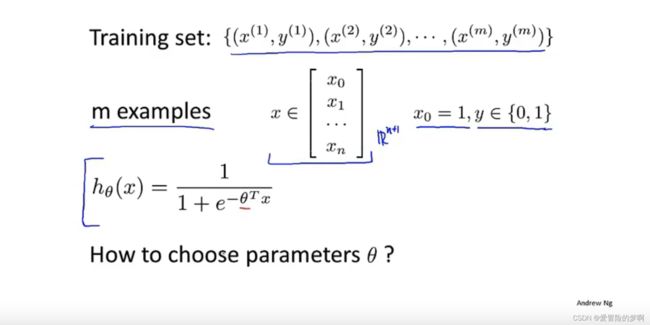
对于一个常规的例子来说,我们有m个数据,m个例子,通常我们把它写作n+1维的向量,x0的那一个是1,下面是假设函数,我们做的就是如何选择假设函数的参数θ,或者说如何拟合参数θ。
对于代价函数,我们之前线性回归的代价函数是这样表示的,这里我们改一下,把1/2放后面,把后面的全部改成cost,这个cost就等于1/2的平方误差,对于这个代价函数的理解就是对于实际值为y,但是算法给出的预测值为y1,那就要让这个算法付出代价,就是cost。但是这里是用在线性回归上的,我们想把它用在逻辑回归上面,如果再使用这个代价函数,它会变成参数θ的非凸函数,这里的非凸函数是指对于一个代价函数J(θ)对于逻辑回归来说,这里的h函数是非线性的,因为是sigmoid函数。把sigmoid函数带入画出的代价函数很复杂,会有很多局部最优解,这就是个非凸函数。相反我们希望我们的代价函数是个凸函数。所以我们要找一个不同的代价函数,它是凸函数。
- 当y=1的时候,就是实际的标签等于1的时候
这里的代价函数就是我们要用到逻辑回归上的,可以画出一个图像来。
如果假设函数预测值是1,而且y刚好等于我预测的,那么这个代价值是0,
因为我们预测对了。
如果h(x)趋于0,当假设函数的输出趋于0的时候,代价值激增,并且趋于无穷,因为预测错了(因为这里有前提条件就是y=1)所以h(x)趋于0正好和实际相反,所以说预测正好相反,代价很大,所以我们要用很大的代价来惩罚这个函数。
- 当y=0的时候,也就是实际为0的时候

和上面相反,因为这里的y=0,所以h(x)输出1的时候,实际预测的与真实的正好相反,所以代价在1处很大。
6.5 简化代价函数与梯度下降
这一节讲我们怎么简化代价函数,以及如何使用梯度下降来对参数进行优化。
为了简化,我们可以把这个代价函数合起来写,并且进行梯度下降。
这个合起来的式子是怎么写的呢?
我们知道y=0或者1,我们假设y=1的时候,后面1-y等于0,后面就没有了,前面把y=1带入和上面分着的式子是一样的。y=0的时候,前面就没有了,这样把0带入后面,也是和单独的式子是一样的。
这里的公式有点错误,就是求和符号应该在外面
这里的代价函数其实是根据统计学中的极大似然估计函数得来得,除了处理方便外,它还是凸函数,方便我们进行梯度下降来优化。本来极大似然函数是正的,这里说的是cost,取负来表示cost,cost越小代表预测的与真实的之间误差越小。
为了找到合适的θ,我们要对这个代价函数进行优化,最小化这个代价函数,这样我们才能拟合出θ

这个对cost的优化,用梯度下降的方式。建议自己推一下,下面是别人推的两个链接。
https://blog.csdn.net/weixin_42234769/article/details/86897353
https://www.jianshu.com/p/610859e27f66
假设你有n个特征,那么你就有一个参数向量θ,从θ0一直到θn,然后用下面式子同时更新所有的θ。我们可以看出来这个梯度下降的式子实际 上和线性回归的式子是一样的。但是看起来是一样的,但是假设函数已经发生了改变,线性回归中假设函数h(x)=θ的转置×x,这里是带入了sigmoid的函数了,所以实际上这两个函数是不同的。
之前我们讲了如何监控梯度下降来保证收敛,同样这里是运用这种方法,来保证收敛。
6.6 高级优化
下面介绍了几种比梯度下降更好的方法,研究生课程中最优化会讲。
他们相比于梯度下降,他们不用手动选择学习率,他们内部有循环,可以自动尝试不同的学习率并且自动选择一个好的学习率。缺点就是太复杂了。
blog.csdnimg.cn/06027f4ab7a4422ca8db8f9c3614fee4.png)
下面举例说明怎么用的这些算法(代码是octave那个语言写的)
就是先求代价函数,然后再求导。

6.7 多元分类 一对多
本节讲如何利用逻辑回归来解决多分类问题。
多分类问题就是不是是与否的问题了,而是有更多的选项

也就是如图所示,标签不是0/1了,而是有很多个了。
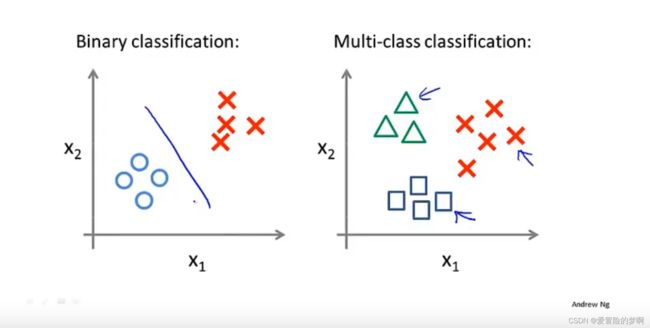
如何来处理多分类问题呢?这里我们用了一个很巧的方法,对于三个类别,我们可以固定住一类,剩下的两类看作一类,这样多类又转换成了两类,然后继续这样操作,直到所有类都固定住即可。

对于任意的输入x,我们选择它属于概率最大的类作为它的标签。