吴恩达机器学习笔记:逻辑回归分类、神经网络
机器学习笔记:逻辑回归分类、神经网络
-
-
-
- 逻辑回归Logistic Regression (不是很懂)
- 正则化Regularization
- 神经网络Neural Networks(也不太懂)
- 建议
- 评估假设算法
- 模型选择和交叉验证集
- 诊断偏差和方差
- 正则化和偏差/方差
- 学习曲线
- 决定下一步做什么
- 机器学习系统的设计(Machine Learning System Design)
- 类偏斜的误差度量(不太懂)
- 机器学习的数据(不太懂)
- 机器学习的数据(不太懂)
-
-
学习日志 2135周
逻辑回归Logistic Regression (不是很懂)
-
分类
-
因变量(dependent variable)可能属于的两个类分别称为负向类(negative class)和正向类(positive class),则因变量 ,其中 0 表示负向类,1 表示正向类。
-
sigmod函数 g(z) g θ ( z ) g_\theta(z) gθ(z)= 1 1 + e − z \frac{1}{1+e^{-z}} 1+e−z1或 g θ ( x ) g_\theta(x) gθ(x)= 1 1 + e θ T x \frac{1}{1+e^{\theta^{T}x}} 1+eθTx1
-
θ T x = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n \theta^{T}x=\theta_{0}x_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+\dots+\theta_{n}x_{n} θTx=θ0x0+θ1x1+θ2x2+⋯+θnxn
-
决策边界(decision boundary):z=多项式(矩阵形式 z= θ T x \theta^{T}x θTx,g(z)图像,根据z的图像(z与0的大小关系)判断(不太清楚)
-
代价函数
-
梯度下降
-
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J\left( \theta \right)=-\frac{1}{m}\sum\limits_{i=1}^{m}{[{{y}^{(i)}}\log \left( {h_\theta}\left( {{x}^{(i)}} \right) \right)+\left( 1-{{y}^{(i)}} \right)\log \left( 1-{h_\theta}\left( {{x}^{(i)}} \right) \right)]} J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
-
θ j : = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) {\theta_j}:={\theta_j}-\alpha \frac{1}{m}\sum\limits_{i=1}^{m}{({h_\theta}({{x}^{(i)}})-{{y}^{(i)}}){x_{j}}^{(i)}} θj:=θj−αm1i=1∑m(hθ(x(i))−y(i))xj(i)
-
这个式子正是我们用来做线性回归梯度下降的
-
对于线性回归假设函数:
h θ ( x ) = θ T X = θ 0 x 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n {h_\theta}\left( x \right)={\theta^T}X={\theta_{0}}{x_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}} hθ(x)=θTX=θ0x0+θ1x1+θ2x2+...+θnxn
而现在逻辑函数假设函数:
h θ ( x ) = 1 1 + e − θ T X {h_\theta}\left( x \right)=\frac{1}{1+{{e}^{-{\theta^T}X}}} hθ(x)=1+e−θTX1
-
-
一对多分类:
- 将多个类中的一个类标记为正向类,然后将其他所有类都标记为负向类,这个模型记作 h θ ( 1 ) ( x ) h_{\theta}^{(1)}(x) hθ(1)(x)。接着,类似地第我们选择另一个类标记为正向类,再将其它类都标记为负向类,将这个模型记作 h θ ( 2 ) ( x ) h_{\theta}^{(2)}(x) hθ(2)(x),依此类推。 最后我们得到一系列的模型简记为: h θ ( i ) ( x ) = p ( y = i ∣ x ; θ ) h_{\theta}^{(i)}(x)=p(y=i|x;\theta) hθ(i)(x)=p(y=i∣x;θ) 其中: i = 1 , 2 , 3 … , k i=1,2,3\dots,k i=1,2,3…,k
- 最后,为了做出预测,我们给出输入一个新的 x x x值,用这个做预测。在分类器里面输入 x x x ,然后我们选择一个让 h θ ( i ) ( x ) h_{\theta}^{(i)}(x) hθ(i)(x)最大的 i i i,即 max i h θ ( i ) ( x ) \max\limits_{i}h_{\theta}^{(i)}(x) imaxhθ(i)(x)
- 选择出哪一个分类器是可信度最高效果最好的,那么就可认为得到一个正确的分类,无论 i i i值是多少,我们都有最高的概率值,我们预测 y y y就是那个值
正则化Regularization
-
过拟合问题over-fitting
-
处理过拟合问题
- 丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征,或者使用一些模型选择的算法来帮忙(例如PCA)
- 正则化。 保留所有的特征,但是减少参数的大小(magnitude)
-
正则化。设置惩罚
-
上面的回归问题中如果我们的模型是: h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 2 + θ 3 x 3 3 + θ 4 x 4 4 {h_\theta}\left( x \right)={\theta_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}^2}+{\theta_{3}}{x_{3}^3}+{\theta_{4}}{x_{4}^4} hθ(x)=θ0+θ1x1+θ2x22+θ3x33+θ4x44我们可以从之前的事例中看出,正是那些高次项导致了过拟合的产生,所以如果我们能让这些高次项的系数接近于0的话,我们就能很好的拟合了。修改后的代价函数如下:
min θ 1 2 m [ ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + 1000 θ 3 2 + 10000 θ 4 2 ] \underset{\theta }{\mathop{\min }}\,\frac{1}{2m}[\sum\limits_{i=1}^{m}{{{\left( {{h}_{\theta }}\left( {{x}^{(i)}} \right)-{{y}^{(i)}} \right)}^{2}}+1000\theta _{3}^{2}+10000\theta _{4}^{2}]} θmin2m1[i=1∑m(hθ(x(i))−y(i))2+1000θ32+10000θ42]
-
假如我们有非常多的特征,我们并不知道其中哪些特征我们要惩罚,我们将对所有的特征进行惩罚,并且让代价函数最优化的软件来选择这些惩罚的程度。这样的结果是得到了一个较为简单的能防止过拟合问题的假设: J ( θ ) = 1 2 m [ ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n θ j 2 ] J\left( \theta \right)=\frac{1}{2m}[\sum\limits_{i=1}^{m}{{{({h_\theta}({{x}^{(i)}})-{{y}^{(i)}})}^{2}}+\lambda \sum\limits_{j=1}^{n}{\theta_{j}^{2}}]} J(θ)=2m1[i=1∑m(hθ(x(i))−y(i))2+λj=1∑nθj2]
-
θ 0 : = θ 0 − a 1 m ∑ i = 1 m ( ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) ) {\theta_0}:={\theta_0}-a\frac{1}{m}\sum\limits_{i=1}^{m}{(({h_\theta}({{x}^{(i)}})-{{y}^{(i)}})x_{0}^{(i)}}) θ0:=θ0−am1i=1∑m((hθ(x(i))−y(i))x0(i))
-
θ j : = θ j − a [ 1 m ∑ i = 1 m ( ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) + λ m θ j ] {\theta_j}:={\theta_j}-a[\frac{1}{m}\sum\limits_{i=1}^{m}{(({h_\theta}({{x}^{(i)}})-{{y}^{(i)}})x_{j}^{\left( i \right)}}+\frac{\lambda }{m}{\theta_j}] θj:=θj−a[m1i=1∑m((hθ(x(i))−y(i))xj(i)+mλθj]
-
j = 1 , 2 , 3 , … , n j=1,2,3,\dots,n j=1,2,3,…,n
-
-
正规方程求解正则化线性回归模型 θ = ( X T X + λ [ 0 1 1 ⋱ 1 ] ) − 1 X T y \theta=\left(X^{T}X+\lambda \left[\begin{matrix}0 \\ &1 \\ &&1 \\ &&&\ddots \\ &&&&1 \end{matrix}\right]\right)^{-1}X^{T}y θ=⎝⎜⎜⎜⎜⎛XTX+λ⎣⎢⎢⎢⎢⎡011⋱1⎦⎥⎥⎥⎥⎤⎠⎟⎟⎟⎟⎞−1XTy
神经网络Neural Networks(也不太懂)
-
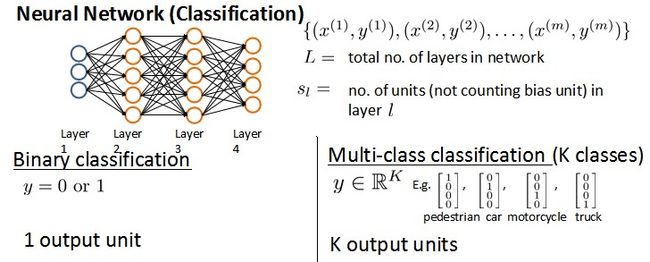
模型表示
- a 1 ( 2 ) = g ( Θ 10 ( 1 ) x 0 + Θ 11 ( 1 ) x 1 + Θ 12 ( 1 ) x 2 + Θ 13 ( 1 ) x 3 ) a_{1}^{(2)}=g(\Theta _{10}^{(1)}{{x}_{0}}+\Theta _{11}^{(1)}{{x}_{1}}+\Theta _{12}^{(1)}{{x}_{2}}+\Theta _{13}^{(1)}{{x}_{3}}) a1(2)=g(Θ10(1)x0+Θ11(1)x1+Θ12(1)x2+Θ13(1)x3)
- a 2 ( 2 ) = g ( Θ 20 ( 1 ) x 0 + Θ 21 ( 1 ) x 1 + Θ 22 ( 1 ) x 2 + Θ 23 ( 1 ) x 3 ) a_{2}^{(2)}=g(\Theta _{20}^{(1)}{{x}_{0}}+\Theta _{21}^{(1)}{{x}_{1}}+\Theta _{22}^{(1)}{{x}_{2}}+\Theta _{23}^{(1)}{{x}_{3}}) a2(2)=g(Θ20(1)x0+Θ21(1)x1+Θ22(1)x2+Θ23(1)x3)
- a 3 ( 2 ) = g ( Θ 30 ( 1 ) x 0 + Θ 31 ( 1 ) x 1 + Θ 32 ( 1 ) x 2 + Θ 33 ( 1 ) x 3 ) a_{3}^{(2)}=g(\Theta _{30}^{(1)}{{x}_{0}}+\Theta _{31}^{(1)}{{x}_{1}}+\Theta _{32}^{(1)}{{x}_{2}}+\Theta _{33}^{(1)}{{x}_{3}}) a3(2)=g(Θ30(1)x0+Θ31(1)x1+Θ32(1)x2+Θ33(1)x3)
- h Θ ( x ) = g ( Θ 10 ( 2 ) a 0 ( 2 ) + Θ 11 ( 2 ) a 1 ( 2 ) + Θ 12 ( 2 ) a 2 ( 2 ) + Θ 13 ( 2 ) a 3 ( 2 ) ) {{h}_{\Theta }}(x)=g(\Theta _{10}^{(2)}a_{0}^{(2)}+\Theta _{11}^{(2)}a_{1}^{(2)}+\Theta _{12}^{(2)}a_{2}^{(2)}+\Theta _{13}^{(2)}a_{3}^{(2)}) hΘ(x)=g(Θ10(2)a0(2)+Θ11(2)a1(2)+Θ12(2)a2(2)+Θ13(2)a3(2))
- X → θ a X\overset{\theta}{\to}a X→θa, θ ⋅ X = a \theta ·X = a θ⋅X=a


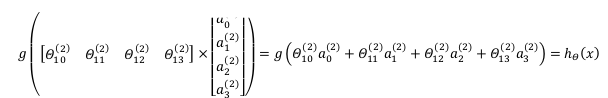
-
多类分类
-
代价函数
- 二类分类 K = 1 K=1 K=1
- K K K类分类( K > 2 K>2 K>2)
- J ( Θ ) = − 1 m [ ∑ i = 1 m ∑ k = 1 k y k ( i ) log ( h Θ ( x ( i ) ) ) k + ( 1 − y k ( i ) ) log ( 1 − ( h Θ ( x ( i ) ) ) k ) ] + λ 2 m ∑ l = 1 L − 1 ∑ i = 1 s l ∑ j = 1 s l + 1 ( Θ j i ( l ) ) 2 J(\Theta) = -\frac{1}{m} \left[ \sum\limits_{i=1}^{m} \sum\limits_{k=1}^{k} {y_k}^{(i)} \log {(h_\Theta(x^{(i)}))}_{k} + \left( 1 - y_k^{(i)} \right) \log \left( 1- {\left( h_\Theta \left( x^{(i)} \right) \right)}_{k} \right) \right] + \frac{\lambda}{2m} \sum\limits_{l=1}^{L-1} \sum\limits_{i=1}^{s_l} \sum\limits_{j=1}^{s_l+1} \left( \Theta_{ji}^{(l)} \right)^2 J(Θ)=−m1[i=1∑mk=1∑kyk(i)log(hΘ(x(i)))k+(1−yk(i))log(1−(hΘ(x(i)))k)]+2mλl=1∑L−1i=1∑slj=1∑sl+1(Θji(l))2
- 这个看起来复杂很多的代价函数背后的思想还是一样的,我们希望通过代价函数来观察算法预测的结果与真实情况的误差有多大,唯一不同的是,对于每一行特征,我们都会给出 K K K个预测,基本上我们可以利用循环,对每一行特征都预测 K K K个不同结果,然后在利用循环在 K K K个预测中选择可能性最高的一个,将其与 y y y中的实际数据进行比较。
- 正则化的那一项只是排除了每一层 θ 0 \theta_{0} θ0后,每一层的 θ \theta θ矩阵的和。最里层的循环 j j j循环所有的行(由 s l s_{l} sl +1 层的激活单元数决定),循环 i i i则循环所有的列,由该层( s l s_{l} sl层)的激活单元数所决定。即: h θ ( x ) h_{\theta}(x) hθ(x)与真实值之间的距离为 每 个 样 本 − 每 个 类 输 出 的 和 每个样本-每个类输出的和 每个样本−每个类输出的和,对参数进行regularization的bias项处理所有参数的平方和。(看不懂)
-
反向传播(不太懂)
-
δ ( l ) = ( Θ ( l ) ) T δ ( l + 1 ) ∗ g ′ ( z ( l ) ) \delta^{(l)}=(\Theta^{(l)})^{T}\delta^{(l+1)}\ast g'(z^{(l)}) δ(l)=(Θ(l))Tδ(l+1)∗g′(z(l))
-
g ′ ( z ( l ) = a l ⋅ ( 1 − a l ) g'(z^{(l)}=a^{l}·(1-a^{l}) g′(z(l)=al⋅(1−al)
-
∂ ∂ Θ i j ( l ) J ( Θ ) = a j ( l ) δ i l + 1 \frac{\partial}{\partial\Theta_{ij}^{(l)}}J(\Theta)=a_{j}^{(l)} \delta_{i}^{l+1} ∂Θij(l)∂J(Θ)=aj(l)δil+1
-
∂ ∂ Θ J ( Θ ) = δ l + 1 ( a ( l ) ) T \frac{\partial}{\partial\Theta}J(\Theta)=\delta^{l+1}(a^{(l)} )^{T} ∂Θ∂J(Θ)=δl+1(a(l))T
-
Δ \Delta Δ是大写的 δ \delta δ
-
在求出了 Δ i j ( l ) \Delta_{ij}^{(l)} Δij(l)之后,我们便可以计算代价函数的偏导数了
-
D i j ( l ) : = 1 m Δ i j ( l ) + λ Θ i j ( l ) , i f j ≠ 0 D_{ij}^{(l)} :=\frac{1}{m}\Delta_{ij}^{(l)}+\lambda\Theta_{ij}^{(l)}, {if} \; j \neq 0 Dij(l):=m1Δij(l)+λΘij(l),ifj=0
-
D i j ( l ) : = 1 m Δ i j ( l ) , i f j = 0 D_{ij}^{(l)} :=\frac{1}{m}\Delta_{ij}^{(l)},{if}\; j = 0 Dij(l):=m1Δij(l),ifj=0
-
∂ ∂ Θ i j ( l ) J ( Θ ) \frac{\partial}{\partial\Theta_{ij}^{(l)}}J(\Theta) ∂Θij(l)∂J(Θ)是 D i j ( l ) D_{ij}^{(l)} Dij(l)
-
l l l 代表目前所计算的是第几层。
j j j代表目前计算层中的激活单元的下标,也将是下一层的第 j j j个输入变量的下标。
i i i代表下一层中误差单元的下标,是受到权重矩阵中第 i i i行影响的下一层中的误差单元的下标。
-
-
梯度检验
-
一个只针对 θ 1 \theta_{1} θ1进行检验的示例:
∂ ∂ θ 1 = J ( θ 1 + ε 1 , θ 2 , θ 3 . . . θ n ) − J ( θ 1 − ε 1 , θ 2 , θ 3 . . . θ n ) 2 ε \frac{\partial}{\partial\theta_1}=\frac{J\left(\theta_1+\varepsilon_1,\theta_2,\theta_3...\theta_n \right)-J \left( \theta_1-\varepsilon_1,\theta_2,\theta_3...\theta_n \right)}{2\varepsilon} ∂θ1∂=2εJ(θ1+ε1,θ2,θ3...θn)−J(θ1−ε1,θ2,θ3...θn)
-
∂ ∂ θ i = J ( θ 1 , θ 2 , θ 3 , … , θ i + ε 1 . . . θ n ) − J ( θ 1 , θ 2 , θ 3 , … , θ i − ε 1 . . . θ n ) 2 ε \frac{\partial}{\partial\theta_i}=\frac{J\left(\theta_1,\theta_2,\theta_3,\dots,\theta_i+\varepsilon_1...\theta_n \right)-J \left( \theta_1,\theta_2,\theta_3,\dots,\theta_i-\varepsilon_1...\theta_n \right)}{2\varepsilon} ∂θi∂=2εJ(θ1,θ2,θ3,…,θi+ε1...θn)−J(θ1,θ2,θ3,…,θi−ε1...θn)
-
-
随机初始化
- 任何优化算法都需要一些初始的参数。到目前为止我们都是初始所有参数为0,这样的初始方法对于逻辑回归来说是可行的,但是对于神经网络来说是不可行的。
- 如果我们令所有的初始参数都为0,这将意味着我们第二层的所有激活单元都会有相同的值。同理,如果我们初始所有的参数都为一个非0的数,结果也是一样的。
- 通常初始参数为正负ε之间的随机值
-
总结神经网络时的步骤:
- 网络结构:
- 第一件要做的事是选择网络结构,即决定选择多少层以及决定每层分别有多少个单元。
- 第一层的单元数即我们训练集的特征数量。最后一层的单元数是我们训练集的结果的类的数量。
- 如果隐藏层数大于1,确保每个隐藏层的单元个数相同,通常情况下隐藏层单元的个数越多越好。
- 我们真正要决定的是隐藏层的层数和每个中间层的单元数。
- 训练神经网络:
- 参数的随机初始化
- 利用正向传播方法计算所有的 h θ ( x ) h_{\theta}(x) hθ(x)
- 编写计算代价函数 J ( θ ) J(\theta) J(θ)的代码
- 利用反向传播方法计算所有偏导数
- 利用数值检验方法检验这些偏导数
- 使用优化算法来最小化代价函数
- 网络结构:
建议
-
当我们运用训练好了的模型来预测未知数据的时候发现有较大的误差,我们下一步可以做什么?
- 获得更多的训练样本——通常是有效的,但代价较大,下面的方法也可能有效,可考虑先采用下面的几种方法。
- 尝试减少特征的数量
- 尝试获得更多的特征
- 尝试增加多项式特征
- 尝试减少正则化程度 λ \lambda λ
- 尝试增加正则化程度 λ \lambda λ
-
运用一些机器学习诊断法来帮助我们知道哪些方法对我们的算法是有效的
评估假设算法
-
避免过拟合和欠拟合
-
训练集和测试集
-
测试集评估在通过训练集让我们的模型学习得出其参数后,对测试集运用该模型,我们有两种方式计算误差:
- 对于线性回归模型,我们利用测试集数据计算代价函数
- 对于逻辑回归模型,我们除了可以利用测试数据集来计算代价函数外:
J t e s t ( θ ) = − 1 m t e s t ∑ i = 1 m t e s t [ log h θ ( x t e s t ( i ) ) + ( 1 − y t e s t ( i ) ) log h θ ( x t e s t ( i ) ) ] J_{test}{(\theta)} = -\frac{1}{{m}_{test}}\sum\limits_{i=1}^{m_{test}} [\log{h_{\theta}(x^{(i)}_{test})}+(1-{y^{(i)}_{test}})\log{h_{\theta}(x^{(i)}_{test})}] Jtest(θ)=−mtest1i=1∑mtest[loghθ(xtest(i))+(1−ytest(i))loghθ(xtest(i))]
误分类的比率,对于每一个测试集样本,计算:
(错误的标记为1)然后对计算结果求平均。
模型选择和交叉验证集
-
显然越高次数的多项式模型越能够适应我们的训练数据集,但是适应训练数据集并不代表着能推广至一般情况,我们应该选择一个更能适应一般情况的模型。
-
我们需要使用交叉验证集来帮助选择模型。 即:使用60%的数据作为训练集,使用 20%的数据作为交叉验证集,使用20%的数据作为测试集
-
模型选择的方法为:
- 使用训练集训练出10个模型
- 用10个模型分别对交叉验证集计算得出交叉验证误差(代价函数的值)
- 选取代价函数值最小的模型
- 用步骤3中选出的模型对测试集计算得出推广误差(代价函数的值)
-
J t r a i n ( θ ) = 1 2 m t r a i n ∑ i = 1 m ( h θ ( x t r a i n ( i ) ) − y t r a i n ( i ) ) 2 J_{train}(\theta) = \frac{1}{2m_{train}}\sum\limits_{i=1}^{m}(h_{\theta}(x^{(i)}_{train})-y^{(i)}_{train})^2 Jtrain(θ)=2mtrain1i=1∑m(hθ(xtrain(i))−ytrain(i))2
-
J c v ( θ ) = 1 2 m c v ∑ i = 1 m ( h θ ( x c v ( i ) ) − y c v ( i ) ) 2 J_{cv}(\theta) = \frac{1}{2m_{cv}}\sum\limits_{i=1}^{m}(h_{\theta}(x^{(i)}_{cv})-y^{(i)}_{cv})^2 Jcv(θ)=2mcv1i=1∑m(hθ(xcv(i))−ycv(i))2
-
J t e s t ( θ ) = 1 2 m t e s t ∑ i = 1 m t e s t ( h θ ( x c v ( i ) ) − y c v ( i ) ) 2 J_{test}(\theta)=\frac{1}{2m_{test}}\sum\limits_{i=1}^{m_{test}}(h_{\theta}(x^{(i)}_{cv})-y^{(i)}_{cv})^2 Jtest(θ)=2mtest1i=1∑mtest(hθ(xcv(i))−ycv(i))2
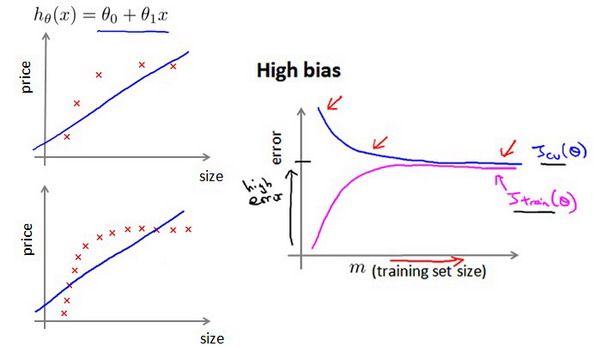
诊断偏差和方差
- 高偏差和高方差的问题基本上来说是欠拟合和过拟合的问题
- 通常会通过将训练集和交叉验证集的代价函数误差与多项式的次数绘制在同一张图表上来帮助分析:

- 对于训练集,当 d d d较小时,模型拟合程度更低,误差较大;随着 d d d的增长,拟合程度提高,误差减小。 对于交叉验证集,当 d d d较小时,模型拟合程度低,误差较大;但是随着 d d d的增长,误差呈现先减小后增大的趋势,转折点是我们的模型开始过拟合训练数据集的时候。
正则化和偏差/方差
-
在我们在训练模型的过程中,一般会使用一些正则化方法来防止过拟合。但是我们可能会正则化的程度太高或太小了,即我们在选择λ的值时也需要思考与刚才选择多项式模型次数类似的问题。
-
我们选择一系列的想要测试 λ \lambda λ值,通常是 0-10之间的呈现2倍关系的值
-
选择 λ \lambda λ的方法为:
-
当 λ \lambda λ较小时,训练集误差较小(过拟合)而交叉验证集误差较,随着 λ \lambda λ的增加,训练集误差不断增加(欠拟合),而交叉验证集误差则是先减小后增加
学习曲线
-
学习曲线来判断某一个学习算法是否处于偏差、方差问题。学习曲线是学习算法的一个很好的合理检验(sanity check)。
-
学习曲线是将训练集误差和交叉验证集误差作为训练集样本数量( m m m)的函数绘制的图表
-
思想:当训练较少行数据的时候,训练的模型将能够非常完美地适应较少的训练数据,但是训练出来的模型却不能很好地适应交叉验证集数据或测试集数据。
-
如何利用学习曲线识别高偏差/欠拟合:
-
如何利用学习曲线识别高方差/过拟合:
决定下一步做什么
- 获得更多的训练样本——解决高方差
- 尝试减少特征的数量——解决高方差
- 尝试获得更多的特征——解决高偏差
- 尝试增加多项式特征——解决高偏差
- 尝试减少正则化程度λ——解决高偏差
- 尝试增加正则化程度λ——解决高方差
- 使用较小的神经网络,类似于参数较少的情况,容易导致高偏差和欠拟合,但计算代价较小
- 使用较大的神经网络,类似于参数较多的情况,容易导致高方差和过拟合,虽然计算代价比较大,但是可以通过正则化手段来调整而更加适应数据。
- 通常选择较大的神经网络并采用正则化处理会比采用较小的神经网络效果要好。
- 对于神经网络中的隐藏层的层数的选择,通常从一层开始逐渐增加层数。
- 为了更好地作选择,可以把数据分为训练集、交叉验证集和测试集,针对不同隐藏层层数的神经网络训练神经网络, 然后选择交叉验证集代价最小的神经网络。
机器学习系统的设计(Machine Learning System Design)
- 构建一个学习算法的推荐方法为:
- 从一个简单的能快速实现的算法开始,实现该算法并用交叉验证集数据测试这个算法
- 绘制学习曲线,决定是增加更多数据,或者添加更多特征,还是其他选择
- 进行误差分析:人工检查交叉验证集中我们算法中产生预测误差的样本,看看这些样本是否有某种系统化的趋势
类偏斜的误差度量(不太懂)
-
类偏斜情况表现为我们的训练集中有非常多的同一种类的样本,只有很少或没有其他类的样本。
-
正确肯定(True Positive,TP):预测为真,实际为真
-
正确否定(True Negative,TN):预测为假,实际为假
-
错误肯定(False Positive,FP):预测为真,实际为假
-
错误否定(False Negative,FN):预测为假,实际为真
-
查准率(Precision)=TP/(TP+FP) 预测为真中的正确率
-
查全率(Recall)=TP/(TP+FN) 预测为真占实际为真中的比例
-
假使,我们的算法输出的结果在0-1 之间,我们使用阀值0.5 来预测真和假。
-
如果我们希望只在非常确信的情况下预测为真,即我们希望更高的查准率,我们可以使用比0.5更大的阀值,如0.7,0.9。减少错误预测情况,同时却会增加未能成功预测情况。
-
如果我们希望提高查全率,尽可能地预测所有有可能是真的情况,我们可以使用比0.5更小的阀值,如0.3。
-
一个帮助我们选择这个阀值的方法。一种方法是计算F1 值(F1 Score),其计算公式为: F 1 S c o r e : 2 P R P + R {{F}_{1}}Score:2\frac{PR}{P+R} F1Score:2P+RPR,我们选择使得F1值最高的阀值。( P P P查准率, R R R查全率)
机器学习的数据(不太懂)
-
什么时候希望获得更多的数据而非修改算法
- 训练集大
- 参数多
- 训练集比参数还要多
- 有足够好的特征/带来有用的信息
-
如果训练集比参数的数量还大,甚至是更多,那么这些算法就不太可能会过度拟合。也就是说训练误差有希望接近测试误差
值,如0.3。 -
一个帮助我们选择这个阀值的方法。一种方法是计算F1 值(F1 Score),其计算公式为: F 1 S c o r e : 2 P R P + R {{F}_{1}}Score:2\frac{PR}{P+R} F1Score:2P+RPR,我们选择使得F1值最高的阀值。( P P P查准率, R R R查全率)
机器学习的数据(不太懂)
- 什么时候希望获得更多的数据而非修改算法
- 训练集大
- 参数多
- 训练集比参数还要多
- 有足够好的特征/带来有用的信息
- 如果训练集比参数的数量还大,甚至是更多,那么这些算法就不太可能会过度拟合。也就是说训练误差有希望接近测试误差
- 通过确保有一个具有很多参数的学习算法来解决,以便我们能够得到一个较低偏差的算法,并且通过用非常大的训练集来保证
返回目录