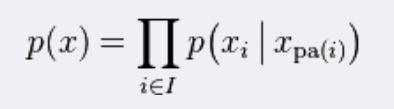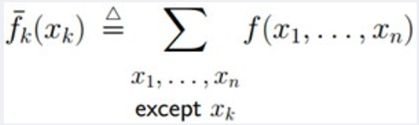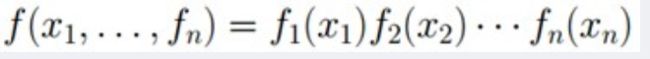朴素贝叶斯、贝叶斯网络分类器
目录
贝叶斯定理 贝叶斯分类
朴素贝叶斯分类器 贝叶斯网络 VS 朴素贝叶斯
贝叶斯网络 条件概率表集合
贝叶斯网络的构造 贝叶斯网络推理的算法之一
贝叶斯网络的三种结构形式
顺连:head-to-tail条件独立 分连:tail-to-tail条件独立 汇连:head-to-head条件独立
因子图 如何把贝叶斯网络(和马尔科夫随机场)转换成因子图
Sum-product算法
如何由联合概率分布求边缘概率分布 sum-product算法
估计类别下特征属性划分的条件概率及Laplace校准 连续型特征属性和零概率事件处理
ABSTRACT
贝叶斯定理
贝叶斯分类
朴素贝叶斯分类器
A classifier is, a function that assigns a class label to instances described by a set of attributes.
分类器训练阶段的任务就是生成分类器,主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率估计,并将结果记录。其输入是特征属性和训练样本,输出是分类器。
naive Bayesian classifier 从训练数据中学习给定类标签C的每个属性Ai的条件概率,再通过应用贝叶斯规则来计算给定A1,...,An的特定实例的C的概率,然后使用 最高的后验概率来预测分类。
强的概率独立性假设使该计算可行:给定C类的值,所有属性Ai在条件上是独立的。
朴素贝叶斯的前提:每个随机变量(特征属性)都是相互独立的。
贝叶斯网络 VS 朴素贝叶斯
贝叶斯网络
Bayesian networks (Pearl, 1988).贝叶斯网络图中的每个顶点表示随机变量,边表示变量之间的直接相关性。
1.一个贝叶斯网络定义包括一个有向无环图(DAG)和一个条件概率表集合(CPT)。DAG的结点V包括随机变量(类别和特征),可以是可直接观测变量或隐藏变量,有向连接E(A->B)表示随机变量间的条件依赖( 结点A是结点B的parent ),且B与A是有依赖关系的(不独立)。条件概率表中的每一个元素对应DAG中唯一的节点,存储此节点对于其所有直接前驱节点的联合条件概率。
贝叶斯网络通过一个有向无环图来表示一组随机变量跟它们的条件依赖关系。它通过条件概率分布来参数化。每一个结点都通过P(node|Pa(node))来参数化,Pa(node)表示网络中的父节点。
条件概率表集合
贝叶斯网络引入了一个条件性独立(conditional independence)概念:即图中任意结点v在给定v的parent结点的情况下,与图中其它结点都是独立的,也就是说P(v|par(v),x1,x2...,xn) = P(v|par(v))。par(v)表示v的parent结点集,x1,x2,...,xn表示图中其它结点。
当特征集合过大(>10)时几乎无法通过统计得到联合概率分布。
贝叶斯分类方法是一种展现已知数据集属性分布的方法,其最终计算结果完全依赖于训练样本中类别和特征的分布。与SVM等分类方法不同,它只是 try to honestly model what's going on。
朴素贝叶斯中对于若干条件概率值不存在的问题,一般通过将所有的概率值加1来解决。
1.定量描述随机变量(特征属性)之间的关系时,需要一些训练所得的数据用来表示每个节点对其直接前驱节点的条件概率,没有前驱节点的节点则使用先验概率表示。如果给出所有节点的条件概率表(可以通过样本训练得到)。和各节点之间的关系,就可以用贝叶斯网络算出每个节点发生的概率。
2.不同的序列,会得到不同的网络结构图:通常我们通过因果关系来决定变量顺序.
贝叶斯网络的构造
2.构造与训练贝叶斯网络分为以下两步:
1、确定随机变量间的拓扑关系,形成DAG。这一步通常需要领域专家完成,而想要建立一个好的拓扑结构,通常需要不断迭代和改进才可以。
2、训练贝叶斯网络参数——估计出各节点的条件概率表。这一步也就是要完成条件概率表的构造,如果每个随机变量的值都是可以直接观察的,那么这一步的训练是直观的,方法类似于朴素贝叶斯分类。但是通常贝叶斯网络的中存在隐藏变量节点,那么训练方法就是比较复杂,例如使用梯度下降法
一般情况先,多变量非独立联合条件概率分布有如下计算公式:
贝叶斯网络有一条极为重要的性质:每一个节点在其直接前驱节点的值确定后,这个节点条件独立于其所有非直接前驱父辈节点。因此,任意随机变量组合的联合条件概率分布被化简:
使用方法上,贝叶斯网络主要用于概率推理及决策,具体来说,就是在信息不完备的情况下通过可以观察随机变量推断不可观察的随机变量,并且不可观察随机变量可以多于以一个,一般初期将不可观察变量置为随机值,然后进行概率推理。
贝叶斯网络推理的算法之一
注:通过因果关系,就能构造网络图。贝叶斯网络参数就是各变量的概率分布,一般是通过训练样本统计获得。
贝叶斯网络的三种结构形式
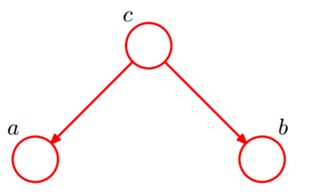
考虑两个变量a和b通过3个变量c间接相连的这一基本情况,可以分为3个子形式:顺连、分连、汇连
顺连:head-to-tail条件独立
如右图所示, 即在c已知的情况下,对a了解不会影响c的信度,进而也不会影响b的信度,a、b之间的信息通道是被阻塞、被阻断的(blocked),a、b是相互独立的。但是在c未知的情况下,对a的了解对影响关于c的信度,进而影响关于b的信度。
顺连又叫head-to-tail条件独立,是个链式网络。
分连:tail-to-tail条件独立
有P(a,b,c)=P(c)*P(a|c)*P(b|c),则:P(a,b|c)=P(a,b,c)/P(c),然后将P(a,b,c)=P(c)*P(a|c)*P(b|c)带入上式,得到:P(a,b|c)=P(a|c)*P(b|c)。
在c未知的情况下,信息可以在a、b之间传递,他们是关联的,在c已知的情况下,信息不能在a、b之间传递,他们是被阻断的,a、b是相互独立的
汇连:head-to-head条件独立
由P(a,b,c) = P(a)*P(b)*P(c|a,b)化简后得
在c已知的情况下,a、b是相互关联的。 在c未知的情况下,a、b被阻断(blocked),是独立的。
又叫head-to-head,汇连是条件依赖的(C依赖于A、B的联合分布)也称为一个v-结构。
更具普遍意义的贝叶斯网络在特征彼此不独立情况下可进行建模。贝叶斯分类方法是一种展现已知数据集属性分布的方法,其最终计算结果完全依赖于训练样本中类别和特征的分布。与SVM等分类方法不同,它只是对事实进行展现。
因子图
因子图,贝叶斯网络,马尔可夫随机场都是概率图(求某个变量的边缘分布是其常见的问题)。可以把贝叶斯网络或马尔科夫随机场转换成因子图,基于因子图可以用sum-product 算法高效的求各个变量的边缘分布。
(wikipedia)因子图的定义:将一个具有多变量的全局函数因子分解,得到几个局部函数的乘积,以此为基础得到的一个双向图叫做因子图(Factor Graph)
因子图就是对函数进行因子分解得到的一种概率图。一般内含两种节点,变量节点和函数节点。一个全局函数通过因式分解能够分解为多个局部函数的乘积,这些局部函数和对应的变量关系就体现在因子图上。
变量之间的关系可以是条件概率或其他关系(如马尔可夫随机场Markov Random Fields中的势函数)。
在因子图中,所有顶点不是变量节点就是函数节点,边线表示它们之间的函数关系。
有一个全局函数,其因式分解方程为
为了方便表示,可以写成
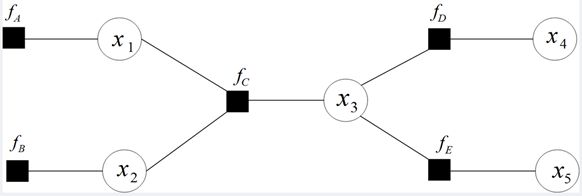
其对应的因子图为:
且上述因子图等价于:
如何把贝叶斯网络(和马尔科夫随机场)转换成因子图
给定下图所示的贝叶斯网络或马尔科夫随机场:
根据各个变量对应的关系,可得:
其对应的因子图为(以下两种因子图的表示方式皆可)
举例子:对于如下的一个因子图:
对于下图所示的马尔科夫链:
对于如下图所示的隐马尔科夫模型:
Sum-product算法
如何由联合概率分布求边缘概率分布
换言之,如果有
那么有
假定现在我们需要计算计算如下式子的结果:
同时,f 能被分解如下:
借鉴分配率,我们可以提取公因子
因为变量的边缘概率等于所有与他相连的函数传递过来的消息的积,所以计算得到:
上述计算过程用到了类似“消息传递”的观点,且总共两个步骤。 第一步、对于f 的分解图,根据蓝色虚线框、红色虚线框围住的两个box外面的消息传递得:
第二步、根据上图的蓝色虚线框、红色虚线框围住的两个box内部的消息传递:
上述计算过程将一个概率分布写成两个因子的乘积,而这两个因子可以继续分解或者通过已知得到。这种利用消息传递的观念计算概率的方法便是sum-product算法。可用于高效求解各个变量的边缘分布 。
sum-product算法
sum-product算法,也叫belief propagation,有两种消息:
一种是变量(Variable)到函数(Function) 的消息:![]() ;
;
另外一种是函数(Function)到变量(Variable)的消息:![]() ;
;
以下是sum-product算法的总体框架
1、给定如下图所示的因子图:
2、sum-product 算法的消息计算规则为:
3、根据sum-product定理,如果因子图中的函数f 没有周期,则有:
注:如果因子图是无环的,则一定可以准确的求出任意一个变量的边缘分布,如果是有环的,则无法用sum-product算法准确求出来边缘分布。
下图所示的贝叶斯网络:
其转换成因子图后,为
若贝叶斯网络中存在“环”(无向),则因此构造的因子图会得到环。而使用消息传递的思想,这个消息将无限传输下去,不利于概率计算。 解决方法有3个:
1、删除贝叶斯网络中的若干条边,使得它不含有无向环。 比如给定下图中左边部分所示的原贝叶斯网络,可以通过去掉C和E之间的边,使得它重新变成有向无环图,从而成为图中右边部分的近似树结构:
具体变换的过程为最大权生成树算法 MSWT,使树的近似联合概率P‘(x)和原贝叶斯网络的联合概率P(x)的相对熵最小
2、重新构造没有环的贝叶斯网络
3、选择loopy belief propagation算法(可理解为sum-product 算法的递归版本),此算法一般选择环中的某个消息,随机赋个初值,然后用sum-product算法,迭代下去,因为有环,一定会到达刚才赋初值的那个消息,然后更新那个消息,继续迭代,直到没有消息再改变为止。唯一的缺点是不确保收敛,当然,此算法在绝大多数情况下是收敛的。
除了这个sum-product算法,还有一个max-product 算法,它在上面sum-product 算法的基础上把求和符号换成求最大值max的符号!这两个算法也能应用到隐马尔科夫模型hidden Markov models上。
贝叶斯经典著作:《数理统计学简史》,以及《统计决策论及贝叶斯分析 》by James O.Berger
估计类别下特征属性划分的条件概率及Laplace校准
计算各个划分的条件概率P(a|y)是朴素贝叶斯分类的关键性步骤,当特征属性为离散值时,只要很方便的统计训练样本中各个划分在每个类别中出现的频率即可用来估计P(a|y),当特征属性为连续值时,通常假定其值服从高斯分布(也称正态分布)。即:
因此只要计算出训练样本中各个类别中此特征项划分的各均值和标准差,代入上述公式即可得到需要的估计值。![]() 为观察到的属性值。
为观察到的属性值。
当某个类别下某个特征项划分没有出现时P(a|y)=0,分类器质量大大降低。解决方法是引入Laplace校准,对没类别下所有划分的计数加1,使得训练样本集数量充分大时不会对结果产生影响。
连续型特征属性和零概率事件处理
当某个类别下某个特征项划分没有出现时P(a|y)=0
引入拉普拉斯校准:对没类别下所有划分(概率为零的)的计数加1,这样如果训练样本集数量充分大时,并不会对结果产生影响,并且解决了上述频率为零的局面。
ABSTRACT
1.近期实验表明A surprisingly simple Bayesian classifier with strong assumptions of independence among features, called naive Bayes, is competitive with state-of-the-art classifiers such as C4.5。
2.基于学习贝叶斯网络的理论,评估了从数据中引入分类器的方法。These networks are factored representations of probability distributions that generalize the naive Bayesian classifier and explicitly represent statements about independence. 概率分布的因子表示。
3.Tree Augmented Naive Bayes (TAN)方法优于朴素贝叶斯,保持计算简单(不涉及搜索)和表征朴素贝叶斯的鲁棒性。
4.使用加州大学欧文分校存储库,并将这些方法与C4.5,朴素贝叶斯和特征选择的包装wrapper方法进行比较。
的
,评估了从数据中引入分类器的方法。These networks are factored representations of probability distributions that generalize the naive Bayesian classifier and explicitly represent statements about independence. 概率分布的因子表示。
3.Tree Augmented Naive Bayes (TAN)方法优于朴素贝叶斯,保持计算简单(不涉及搜索)和表征朴素贝叶斯的鲁棒性。
4.使用加州大学欧文分校存储库,并将这些方法与C4.5,朴素贝叶斯和特征选择的包装wrapper方法进行比较。