一种基于层次分析法的改进KNN算法
说明
由于是第一次写论文,这篇论文只发表在了本科学校的学报上,在2018年7月12号已经上传知网,在知网网址为:一种基于层次分析法的改进KNN算法代码 。之前忙于整理机器学习笔记,而忽略这篇论文的整理。
前言
本篇论文是对KNN算法的做出的改进,在本篇博客里就不介绍KNN算法的相关介绍,若有需要请移步:机器学习实战——KNN分类算法。同时在论文的实验部分,将本文提出的改进算法与2013年10月肖辉辉和段艳明在将《计算机科学》杂志上发表的《基于属性值相关距离的KNN算法的改进研究》提出的算法做了比较。对于这篇论文的相关内容以及代码请详见:基于属性值相关距离的KNN算法。同时也将论文的所有代码进行了整理并上传了CSDN,如有需要请移步:一种基于层次分析法的改进KNN算法
论文主要内容截图
传统 KNN 算法有一个缺陷,那就是不同属性对分类的影响力度相同即权重相同,本文提出了一种用层次 分 析 法 为 属 性 赋 权 值 的 KNN 算 法,即AHP-KNN 算法,来解决不同不同属性对对分类影响不同的问题。下面是论文中提出的AHP-KNN算法相关内容的截图。

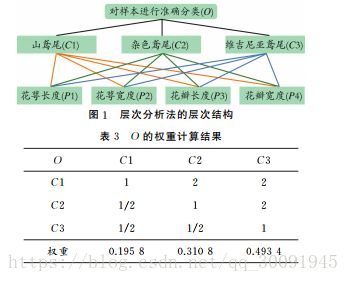

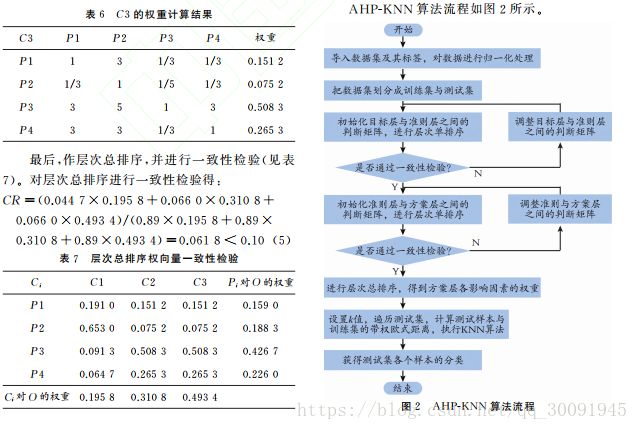
论文代码
由于层次分析法确定权重的过程主要是判断矩阵基本是手动调节,写成代码也不是很方便。因此层分析法的代码就没有此给出。
AHP-KNN的python代码
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time : 2017/6/1 19:28
# @Author : Dai PuWei
# @Site : 计通303实验室
# @File : FCD_KNN.py
# @Software: PyCharm Community Edition
import numpy as np
import operator
class AHP_KNN:
def __init__(self,train_data,train_label,weight):
"""
这是AHP_KNN算法的构造函数
:param train_data: 训练数据集
:param train_label: 训练数据集标签
:param weight: 属性权重
"""
self.Train_data = train_data
self.Train_label = train_label
self.Weight = weight
def predict(self,test_data,k):
"""
这是AHP-KNN算法中测试一组数据的函数
:param test_data: 测试数据
:param k: 邻居数
"""
# 计算测试数据与训练数据之间的欧氏距离
dataSetSize = np.shape(self.Train_data)[0]
diffMat = np.tile(test_data, (dataSetSize, 1)) - self.Train_data
sqDiffMat = diffMat ** 2
sqDiffMat = sqDiffMat*self.Weight
sqDistances = sqDiffMat.sum(axis=1)
distances = sqDistances ** 0.5
# 对分类标签进行统计,找出对测试数据最合适的K个分类
sortedDistIndicies = distances.argsort()
classCount = {}
for i in range(k):
voteIlabel = self.Train_label[sortedDistIndicies[i]]
classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
return sortedClassCount[0][0]
def Test(self,Test_data,k):
"""
这是AHP-KNN算法的测试函数
:param test_data: 测试数据集
:param test_label: 测试数据集标签
:param k: 邻居数
"""
result = [] #存储预测结果
size = np.shape(Test_data)[0]
for i in range(size):
result.append(self.predict(Test_data[i],k))
result = np.array(result)
return result由于本文提出的改进算法与2013年10月肖辉辉和段艳明在将《计算机科学》杂志上发表的《基于属性值相关距离的KNN算法的改进研究》提出的算法做了比较。对于这篇论文的相关内容以及代码请详见:基于属性值相关距离的KNN算法。
传统KNN的python代码
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time : 2017/6/1 19:28
# @Author : Dai PuWei
# @Site : 计通303实验室
# @File : KNN.py
# @Software: PyCharm Community Edition
import numpy as np
import operator
class KNN:
def __init__(self,train_data,train_label):
"""
这是KNN算法的构造函数
:param train_data: 训练数据集
:param train_label: 训练数据集标签
"""
self.Train_data = train_data
self.Train_label = train_label
def predict(self,test_data,k):
"""
这是测试一组数据的函数
:param test_data: 测试数据
:param k: 邻居数
"""
# 计算测试数据与训练数据之间的欧氏距离
dataSetSize = np.shape(self.Train_data)[0]
diffMat = np.tile(test_data, (dataSetSize, 1)) - self.Train_data
distances = np.sum(diffMat**2,1)** 0.5
# 对分类标签进行统计,找出对测试数据最合适的K个分类
sortedDistIndicies = distances.argsort()
classCount = {}
for i in range(k):
voteIlabel = self.Train_label[sortedDistIndicies[i]]
classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
return sortedClassCount[0][0]
def Test(self,Test_data,k):
"""
这是KNN算法的测试函数
:param test_data: 测试数据集
:param k: 邻居数
"""
result = [] #存储预测结果
for test_data in Test_data:
result.append(self.predict(test_data,k))
result = np.array(result)
return result实验结果
测试不同k 值对分类结果的影响
该实验样本取150组,k 值为首项为1、公差为1的等差数列,数列最后一项为100。利用 Pycharm软件仿真得到不同k 值下的误差率,结果如下图所示。

从图 3 可 以 看 出,k 值 在 20~60 时,AHP-KNN 算 法 的 误 差 率 小 于 FCD-KNN 算 法 和 传 统KNN 算 法,AHP-KNN 算 法 的 效 率 比 FCD-KNN算法与传统 KNN 算法的效率高;k 值大于60时,AHP-KNN 算法的误差率开始逐步增大,效率开始
降低。从图3中还可以得出,在k 值较小的情况下(具体到鸢尾花数据集就是k 值小于数据集大小的1/3时)误差较小,效率较高。
测试训练样本数量对分类结果的影响
假定k 值为15,该实验的测试样本所占比例从0.30开始,每次增加0.05,直至0.95,训练样本数量不同时的误差率如下图所示。
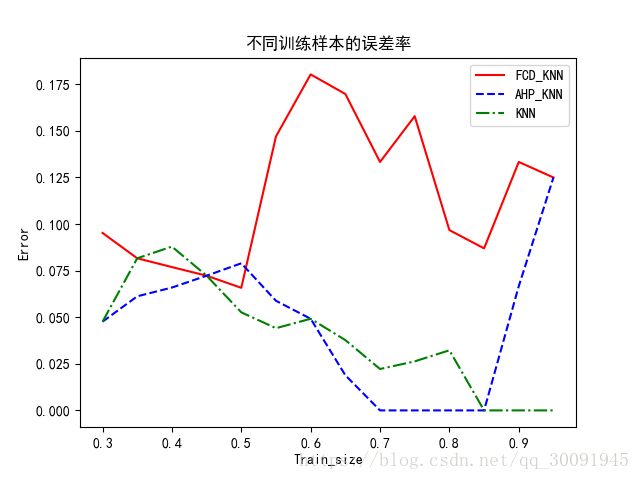
从图4可以看出,随着训练样本数量的不断增加,AHP-KNN 算法的误差逐步降低,效率不断提高,并且逐步优于 FCD-KNN 算法和传统 KNN 的效率。虽然 AHP-KNN 算法的误差率刚开始略高,但是随着训练样本数量的逐步增加,误差率逐渐下降,并且在训练样本比例在小于0.80时基本趋于稳定。因此,在k 值确定的情况下,随着训练样本比率的增加,AHP-KNN 算法比 FCD-KNN 算法更稳定,同 时 AHP-KNN 算 法 的 效 率 也 略 好 于 传 统KNN 算法。