线性回归
曾经有一段往事…
某一天,我想去中国银行贷款,特此向周边的一些朋友询问了下他们的贷款情况,并做了张如下的表:
| 工资 | 年龄 | 额度 |
|---|---|---|
| 4000 | 25 | 20000 |
| 8000 | 32 | 60000 |
| 6000 | 27 | 34000 |
| 7500 | 33 | 50000 |
| 12000 | 39 | 80000 |
通过上述的数据,我想预测下:如果我去银行贷款,银行会贷多少给我呢?如果我要贷50000,银行能贷给我吗?
这里引出两个概念(何为回归?何为分类?):
其一:银行能贷多少给我?这是一个回归问题,回归指的就是通过数据,得到一个预测的值,也就是分析数据,银行能贷多少给我。
其二:如果我要贷50000,银行能贷给我吗?这是一个分类问题,分类指的就是通过数据,最终得到一个唯一的类别值,即银行能贷为1,不能贷0两个类别值。也就是得到我要贷50000,是能贷给我(1)还是不能带给我(0)。
线性回归
现在很是苦恼,因为我只知道工资和年龄两个特征值以及对应的额度,到底我会贷款多少呢?究竟工资和年龄之间有什么关系呢?工资对额度有多少影响?年龄对额度有多少影响?
具体对于关系问题的求解,就是机器学习的核心(寻找数据之间的关系)。
现在我们通过数学来解释这一切:
使用 x 1 x_1 x1, x 2 x_2 x2分别表示年龄和工资, y y y表示额度。
设 θ 1 \theta_1 θ1是年龄的参数, θ 2 \theta_2 θ2是工资的参数,其他因素,使用 θ 0 \theta_0 θ0表示。
借助这个参数,寻找出年龄、工资以及其他因素对于额度的影响大小,最终找到最合适的一条线(想象一个高维)来最好的拟合我们的数据点:
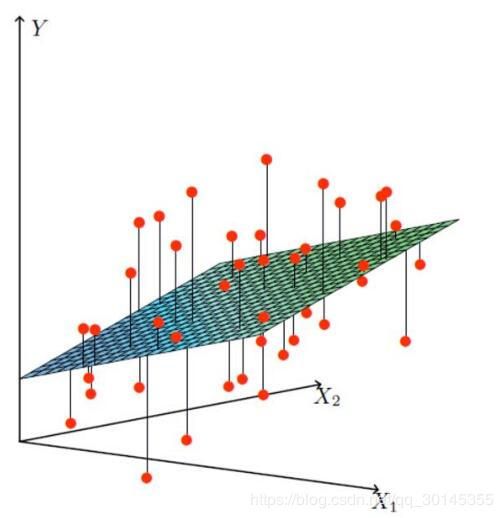
现在就要通过 x 1 , x 2 x_1,x_2 x1,x2来找到一条线或平面来拟合数据,就是找到哪一个平面最接近额度,因为找到这个平面后,只要我知道 x 1 , x 2 x_1,x_2 x1,x2的值后就能知道 y y y的值,也就能知道贷款多少了(当然这个值不会绝对的准确,只能预测不断接近的真相)
综上: y = h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 y=h_\theta(x) = \theta_0+\theta_1x_1+\theta_2x_2 y=hθ(x)=θ0+θ1x1+θ2x2
θ 0 \theta_0 θ0:是偏置项,对最终结果影响小。所谓偏置项,即额度可能会进行浮动,贷款不一定准确,可能多贷一点,可能少贷一点。
θ 1 、 θ 2 \theta_1、\theta_2 θ1、θ2:是权重参数,对最终的结果影响更大(比偏置项大,不难发现 θ 1 、 θ 2 \theta_1、\theta_2 θ1、θ2都乘以了一个 x x x,肯定比偏置项大了)
整合: h θ ( x ) = ∑ 1 n θ i x i = θ T x ( i ) h_\theta(x)=\sum_1^n\theta_ix_i=\theta^Tx^{(i)} hθ(x)=∑1nθixi=θTx(i) (这里默认加入了一个 x 0 x_0 x0的特征,该特征的值恒为1)
这样整合的好处:其一是更加的简洁,其二是更加的规律,便于进行矩阵的运算。
误差问题
真实值和预测值之间肯定是要存在差异的(用 ε \varepsilon ε来表示该误差)
如上图所示:真实值(红点)与预测值之间就存在差异,有些差异是正数有些差异是负数。表示相对于预测的额度值,有时候多贷了或者少贷了一些给客户,而这些差异是可以允许存在的。因为在机器学习中,数据模型和现实肯定存在差异,只是需要我们去合理利用这些差异,来解决我们的问题。
而每个样本都存在误差,即如果我们有一万个样本,就有一万个误差。
现在对于每个样本: y ( i ) = θ T x ( i ) + ε ( i ) y^{(i)}=\theta^Tx^{(i)}+\varepsilon^{(i)} y(i)=θTx(i)+ε(i)————(1)
误差 ε ( i ) \varepsilon^{(i)} ε(i)是独立并同分布,并且服从均值为0方差为 θ 2 \theta^2 θ2的高斯分布
独立:数据之间的独立性。例如张三和李四一起来贷款,银行给张三贷了5000,给李四贷的15000,贷款之间的差异并不会由二人之间的关系产生变化。
同分布:数据来源同一个地方。即张三和李四他俩都来的是我们假定的中国银行。如果我的数据同时有农业银行和中国银行,把两个不同银行的数据拿来混合建立一个模型,显然是不符合实际的。
高斯分布:即正态分布(正常状态下的分布),一种连续型随机变量的概率密度函数。符合高斯分布的原因是,虽然银行可能会多给某人,也可能会少给某人,但是绝大多数情况下这个浮动不会太大,只有极小情况下浮动较大,符合正常情况。
高斯分布图如下:
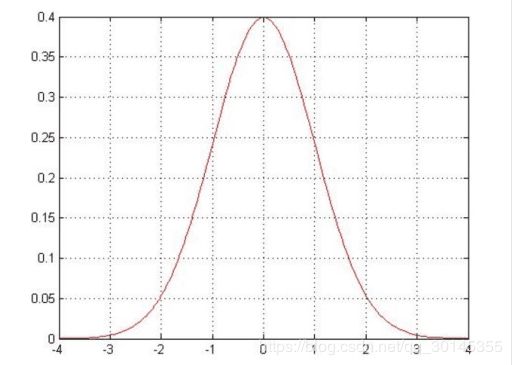
从高斯分布图可知,[-1,1]之间的分布占大部分,表示贷款的额度大多数情况下都是差异不大的,可能只是几百几十的,只有极少情况下[-4,-1]||[1,4]会多贷十万,少贷十万。意味着[-1,1]的贷款额度可能性是比较大的。
问题来了,为什么这些数据一定符合独立、同分布以及高斯分布?有严格的数学证明吗?
答案是没有数学证明,仅仅是提出来的一些假设。因为在机器学习中,你并不能认为一个事就是独立的,就是同分布,就是标准的高斯分布。但是机器学习它是从实际的角度出发,基于实际情况做出假设,大多数情况都是误差较小的,极小情况下误差是比较大的。虽然做的是一个假设,但是最终得到的结果是可利用的,而只要模型可用,则认为这个假设是成立的。
高斯分布的概率密度函数: f ( x ) = 1 2 π σ e − x 2 2 σ 2 f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{x^2}{2\sigma^2}} f(x)=2πσ1e−2σ2x2
而误差服从高斯分布: f ( ϵ ( i ) ) = 1 2 π σ e − ( ϵ ( i ) ) 2 2 σ 2 f(\epsilon^{(i)})=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{({\epsilon^{(i)}})^2}{2\sigma^2}} f(ϵ(i))=2πσ1e−2σ2(ϵ(i))2————(2)
将(1)变形为 ε ( i ) = y ( i ) − θ T x ( i ) \varepsilon^{(i)} = y^{(i)}-\theta^Tx^{(i)} ε(i)=y(i)−θTx(i),带入(2)中得:
f ( y ( i ) ∣ ϵ ( i ) ; θ ) = 1 2 π σ e − ( y ( i ) − θ T x ( i ) ) 2 2 σ 2 f(y^{(i)}|\epsilon^{(i)};\theta)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}} f(y(i)∣ϵ(i);θ)=2πσ1e−2σ2(y(i)−θTx(i))2——(3)
f ( y ( i ) ∣ ϵ ( i ) ; θ ) f(y^{(i)}|\epsilon^{(i)};\theta) f(y(i)∣ϵ(i);θ)参数理解: y [ 已 知 量 ] , ϵ [ 确 定 量 ] , θ [ 自 变 量 ] y[已知量],\epsilon[确定量],\theta[自变量] y[已知量],ϵ[确定量],θ[自变量],左式也可写成 p ( y ( i ) ∣ ϵ ( i ) ; θ ) , 因 为 它 本 身 就 是 一 个 概 率 密 度 函 数 p(y^{(i)}|\epsilon^{(i)};\theta),因为它本身就是一个概率密度函数 p(y(i)∣ϵ(i);θ),因为它本身就是一个概率密度函数
附:概率密度函数的理解
F ( x ) = P ( X ≤ x ) = ∫ − ∞ x f ( x ) d t F(x)=P(X\leq{x})=\int_{-\infty}^{x}f(x)dt F(x)=P(X≤x)=∫−∞xf(x)dt ( − ∞ < x < + ∞ ) (-\infty<x<+\infty) (−∞<x<+∞)
称X为连续型随机变量, f ( x ) f(x) f(x)为X的概率密度函数,简称概率密度。概率密度是为了刻画出连续型随机变量的概率分布规律。
概率密度 f ( x ) f(x) f(x)满足性质:
f ( x ) ≥ 0 , ∫ − ∞ + ∞ f ( x ) d x = 1 , P ( a < X ≤ b ) = ∫ a b f ( x ) d x ) f(x)\geq0,\int_{-\infty}^{+\infty}f(x)dx=1,P(a<X\leq{b})=\int_{a}^{b}f(x)dx) f(x)≥0,∫−∞+∞f(x)dx=1,P(a<X≤b)=∫abf(x)dx)
概率密度在数学上的表示就是积分的运算,积分的面积代表概率的大小。
重要!!!概率密度函数 f ( x ) f(x) f(x)的取值本身并不表示概率,概率密度是分布函数的导数,而分布函数是概率密度的一个特定的原函数。
概率密度应用于连续型随机变量,值域是区间,而离散型随机变量是单个值。
似然函数
假设场景:
今天我想去赌场赌博,但是我不知道我的输赢如何。但是我想,我的输赢应该符合赌场的某种规则,但是这个规则我是并不知道的,此时我该怎么办呢?于是我打算在赌场的门口等待赌完的人出来后,出来一人,我询问下:“哥们儿,今天赢钱了吗?”,结果第一人,第二人…最终十人里面,有九人都表示赢钱,只有一人表示输钱。那么这个时候我就认为,不管这个赌场符合什么样的规则,反正我进去赌博后九成的几率是赢钱,为什么呢?因为我已经通过数据分析,有九成的人都是赢钱,而我和他们都是一样的,所以我基本上也会赢钱。
说白了,以上分析就是传说中的似然函数的目的
似然函数:也是一个概率密度函数 L ( θ ∣ x ) L(\theta|x) L(θ∣x),表示在样本值x已知的情况下求最可能的 θ \theta θ值;实际运用中,根据我们的样本去估计参数值(参数估计),找到最最符合的参数,使得与我们的数据组合后恰好是真实值。
以上说了概率密度函数,概率密度函数的另一种表达方式是 f ( x ∣ θ ) f(x|\theta) f(x∣θ),表示给定参数 θ \theta θ,根据自变量x求因变量f(x)的函数。还有一种表达方式是 f ( y ∣ x ; θ ) 或 p ( y ∣ x ; θ ) f(y|x;\theta)或p(y|x;\theta) f(y∣x;θ)或p(y∣x;θ), y : 已 知 量 , x : 确 定 量 , θ : 自 变 量 y:已知量,x:确定量,\theta:自变量 y:已知量,x:确定量,θ:自变量
两者区别:密度函数是关于x的函数,似然函数是关于 θ \theta θ的函数
对于似然函数的目的理解:当我不知道赌场是符合哪种规则的时候,我就去观测一些数据,用数据找出其中的规则后得到相应的参数,然后将参数和我们的数据组合后,恰好是真实值。就好像得到0.9的参数是赢钱,再结合我自身1,得出我赢钱的几率就是0.9.如何找0.9这个参数就是似然函数的目的。
如今如何使得参数和数据组合后恰好是真实值呢?或者越接近真实值呢?(这其实就是我们的目标)
似然函数: L ( θ ) = 1 2 π σ e − ( y − θ T x ) 2 2 σ 2 L(\theta)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(y-\theta^Tx)^2}{2\sigma^2}} L(θ)=2πσ1e−2σ2(y−θTx)2,然后代入我们的一个样本,自然而然就求出了 θ \theta θ的值,此时引入的问题是,该值是否符合另一个样本呢?答案是否定的,因为这个似然函数只关心了一个样本,似有井底之蛙之嫌。
这里的似然函数就是上述的(3)式
于是我们得到一种可以关联所有样本的似然函数:
L ( θ ) = ∏ i = 1 m p ( y ( i ) ∣ ϵ ( i ) ; θ ) = ∏ i = 1 m 1 2 π σ e − ( y ( i ) − θ T x ( i ) ) 2 2 σ 2 L(\theta)=\prod_{i=1}^mp{(y^{(i)}|\epsilon^{(i)};\theta)}=\prod_{i=1}^m\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}} L(θ)=∏i=1mp(y(i)∣ϵ(i);θ)=∏i=1m2πσ1e−2σ2(y(i)−θTx(i))2
(1~m的累乘表示关心所有的样本)
为什么关联所有的样本就能使用累乘呢?
因为多个样本之间的乘积依然保留原本的分布模式,并且会使常见的概率更常见,并且这个概率对每个样本都有一定的关联性。
对数似然
对数似然出现的原因,是为了简化似然函数中的累乘计算,将累乘转化为累加。
对数似然: log L ( θ ) = log ∏ i = 1 m 1 2 π σ e − ( y ( i ) − θ T x ( i ) ) 2 2 σ 2 \log{L(\theta)}=\log\prod_{i=1}^m\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}} logL(θ)=log∏i=1m2πσ1e−2σ2(y(i)−θTx(i))2
展开化简得:
log L ( θ ) = ∑ i = 1 m log 1 2 π σ e − ( y ( i ) − θ T x ( i ) ) 2 2 σ 2 \log{L(\theta)}=\sum_{i=1}^{m}\log\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}} logL(θ)=∑i=1mlog2πσ1e−2σ2(y(i)−θTx(i))2
= m log 1 2 π − 1 σ 2 × 1 2 × log e × ∑ i = 1 m ( y ( i ) − θ T x ( i ) ) 2 =m\log\frac{1}{\sqrt{2\pi}}-\frac{1}{\sigma^2}\times\frac{1}{2}\times\log{e}\times\sum_{i=1}^{m}(y^{(i)}-\theta^Tx^{(i)})^2 =mlog2π1−σ21×21×loge×∑i=1m(y(i)−θTx(i))2
对数似然函数和似然函数的目标是一致的,而且对数似然并不会影响似然函数的峰值和分布,所以可以使用对数似然来进行简化。
上式中的log我们可以替换为ln,约掉 log e \log{e} loge:
ln L ( θ ) = ∑ i = 1 m ln 1 2 π σ e − ( y ( i ) − θ T x ( i ) ) 2 2 σ 2 = m ln 1 2 π − 1 σ 2 × 1 2 ∑ i = 1 m ( y ( i ) − θ T x ( i ) ) 2 \ln{L(\theta)}=\sum_{i=1}^{m}\ln\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\sigma^2}}=m\ln\frac{1}{\sqrt{2\pi}}-\frac{1}{\sigma^2}\times\frac{1}{2}\sum_{i=1}^{m}(y^{(i)}-\theta^Tx^{(i)})^2 lnL(θ)=∑i=1mln2πσ1e−2σ2(y(i)−θTx(i))2=mln2π1−σ21×21∑i=1m(y(i)−θTx(i))2
再回顾下我们的目标,是为了使似然函数越大越好!
而式中 m ln 1 2 π m\ln\frac{1}{\sqrt{2\pi}} mln2π1为一个常数, 1 2 σ 2 ∑ i = 1 m ( y ( i ) − θ T x ( i ) ) 2 \frac{1}{2\sigma^2}\sum_{i=1}^{m}(y^{(i)}-\theta^Tx^{(i)})^2 2σ21∑i=1m(y(i)−θTx(i))2是一个正数
那么现在的目标转换成如何使得 1 2 σ 2 ∑ i = 1 m ( y ( i ) − θ T x ( i ) ) 2 \frac{1}{2\sigma^2}\sum_{i=1}^{m}(y^{(i)}-\theta^Tx^{(i)})^2 2σ21∑i=1m(y(i)−θTx(i))2的值最小。
得到目标函数: J ( θ ) = 1 σ 2 × 1 2 ∑ i = 1 m ( y ( i ) − θ T x ( i ) ) 2 J(\theta)=\frac{1}{\sigma^2}\times\frac{1}{2}\sum_{i=1}^{m}(y^{(i)}-\theta^Tx^{(i)})^2 J(θ)=σ21×21∑i=1m(y(i)−θTx(i))2(最小二乘法)
化简得: J ( θ ) = 1 2 ( X θ − y ) T ( X θ − y ) J(\theta)=\frac{1}{2}(X\theta-y)^T(X\theta-y) J(θ)=21(Xθ−y)T(Xθ−y)
= 1 2 ( θ T X T θ − θ T X T y − y T X θ + y T y ) =\frac{1}{2} ({\theta^TX^T\theta-\theta^TX^Ty-y^TX\theta+y^Ty}) =21(θTXTθ−θTXTy−yTXθ+yTy)
对 θ \theta θ求偏导得: J ′ ( θ ) = X T X θ − X T y J^{'}(\theta)=X^TX\theta-X^Ty J′(θ)=XTXθ−XTy
J ( θ ) 的 最 小 值 点 就 是 偏 导 为 0 的 点 , 使 J ′ ( θ ) = 0 , 得 : J(\theta)的最小值点就是偏导为0的点,使J^{'}(\theta)=0,得: J(θ)的最小值点就是偏导为0的点,使J′(θ)=0,得:
=> 0 = X T X θ − X T y 0=X^TX\theta-X^Ty 0=XTXθ−XTy
=> X T X θ = X T y X^TX\theta=X^Ty XTXθ=XTy
=> θ = ( X T X ) − 1 X T y \theta=(X^TX)^{-1}X^Ty θ=(XTX)−1XTy
而现在X与y值都是已知的,则 θ \theta θ可求了。
评估方法
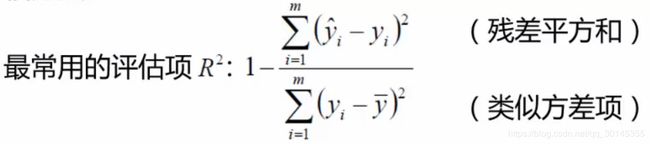
R 2 的 取 值 范 围 越 接 近 1 我 们 认 为 模 型 拟 合 得 越 好 R^2的取值范围越接近1我们认为模型拟合得越好 R2的取值范围越接近1我们认为模型拟合得越好
就得使残差平方和越小越好