scikit-learn Cookbook-2
第二章 处理线性模型
本章包括以下主题:
- [线性回归模型]
- [评估线性回归模型]
- [用岭回归弥补线性回归的不足]
- [优化岭回归参数]
- [LASSO正则化]
- [LARS正则化]
- [用线性方法处理分类问题——逻辑回归]
- [贝叶斯岭回归]
- [用梯度提升回归从误差中学习]
线性模型是统计学和机器学习的基础。很多方法都利用变量的线性组合描述数据之间的关系。
2.1 线性回归模型
我们从最简单的线性回归(Linear regression)开始。线性回归是最早的也是最基本的模型——把数据拟合成一条直线。boston数据集很适合用来演示线性回归。
from sklearn import datasets
boston = datasets.load_boston()
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(boston.data, boston.target)
2.2 评估线性回归模型
在这个主题中,我们将介绍回归模型拟合数据的效果。上一个主题我们拟合了数据,但是并没太关注拟合的效果。每当拟合工作做完之后,我们应该问的第一个问题就是“拟合的效果如何?"
from sklearn import datasets
boston = datasets.load_boston()
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(boston.data, boston.target)
predictions = lr.predict(boston.data)
%matplotlib inline
from matplotlib import pyplot as plt
f, ax = plt.subplots(figsize=(7, 5))
f.tight_layout()
ax.hist(boston.target - predictions,bins=40, label='Residuals Linear',
color='b', alpha=.5);
ax.set_title("Histogram of Residuals")
ax.legend(loc='best');
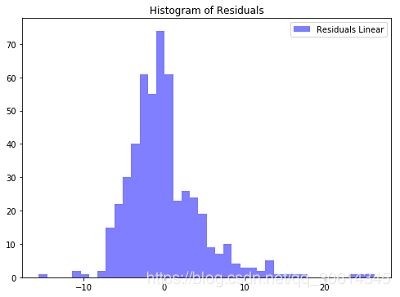
误差项服从均值为0的正态分布。残差就是误差,所以这个图也应该近似正态分布。看起来拟合挺好的,只是有点偏。我们计算一下残差的均值,应该很接近0:
import numpy as np
np.mean(boston.target - predictions)
# 4.296958046296258e-15
另一个图是分位数概率分布,我们用Scipy来实现图形,因为它内置这个概率分布图的方法:
from scipy.stats import probplot
f = plt.figure(figsize=(7, 5))
ax = f.add_subplot(111)
probplot(boston.target - predictions, plot=ax);
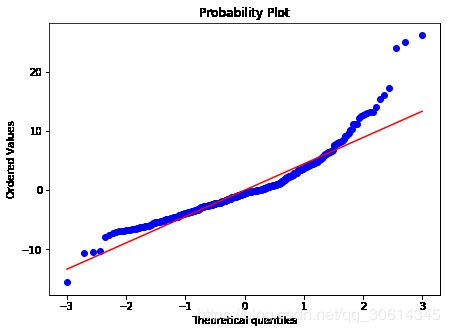
我们还可以观察拟合其他量度,最常用的还有均方误差(mean squared error,MSE),平均绝对误差(mean absolute deviation,MAD)。让我们用Python实现这两个量度。后面我们用scikit-learn内置的量度来评估回归模型的效果:
def MSE(target, predictions):
squared_deviation = np.power(target - predictions, 2)
return np.mean(squared_deviation)
MSE(boston.target, predictions)
# 21.894831181729206
def MAD(target, predictions):
absolute_deviation = np.abs(target - predictions)
return np.mean(absolute_deviation)
MAD(boston.target, predictions)
# 3.270862810900317
相关系数是随机变量,因此它们是有分布的。让我们用bootstrapping(重复试验)来看看犯罪率的相关系数的分布情况。bootstrapping是一种学习参数估计不确定性的常用手段:
n_bootstraps = 1000
len_boston = len(boston.target)
subsample_size = np.int(0.5*len_boston)
subsample = lambda: np.random.choice(np.arange(0, len_boston),size=subsample_size)
coefs = np.ones(n_bootstraps) #相关系数初始值设为1
for i in range(n_bootstraps):
subsample_idx = subsample()
subsample_X = boston.data[subsample_idx]
subsample_y = boston.target[subsample_idx]
lr.fit(subsample_X, subsample_y)
coefs[i] = lr.coef_[0]
f = plt.figure(figsize=(7, 5))
ax = f.add_subplot(111)
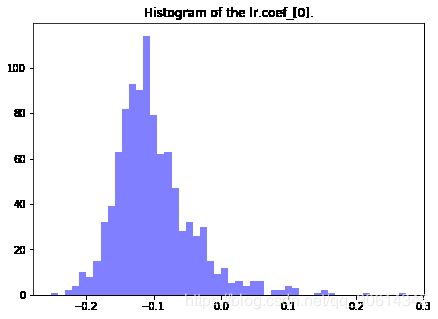
ax.hist(coefs, bins=50, color='b', alpha=.5)
ax.set_title("Histogram of the lr.coef_[0].")
# 我们还想看看重复试验后的置信区间:
np.percentile(coefs, [2.5, 97.5])
# array([-0.18831405, 0.05032466])
置信区间的范围表面犯罪率其实不影响房价,因为0在置信区间里面,表面犯罪率可能与房价无关。值得一提的是,bootstrapping可以获得更好的相关系数估计值,因为使用bootstrapping方法的均值,会比普通估计方法更快地收敛(converge)到真实均值。
2.3 用岭回归弥补线性回归的不足
岭回归和线性回归不同,它引入了正则化参数来“缩减”相关系数。当数据集中存在共线因素时,岭回归会很有用。
# 首先我们用make_regression建一个有3个自变量的数据集,但是其秩为2,
# 因此3个自变量中有两个自变量存在相关性。
from sklearn.datasets import make_regression
reg_data, reg_target = make_regression(n_samples=2000, n_features=3,
effective_rank=2, noise=10)
# 首先,我们用普通的线性回归拟合:
import numpy as np
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
def fit_2_regression(lr):
n_bootstraps = 1000
coefs = np.ones((n_bootstraps, 3))
len_data = len(reg_data)
subsample_size = np.int(0.75*len_data)
subsample = lambda: np.random.choice(np.arange(0, len_data),
size=subsample_size)
for i in range(n_bootstraps):
subsample_idx = subsample()
subsample_X = reg_data[subsample_idx]
subsample_y = reg_target[subsample_idx]
lr.fit(subsample_X, subsample_y)
coefs[i][0] = lr.coef_[0]
coefs[i][1] = lr.coef_[1]
coefs[i][2] = lr.coef_[2]
%matplotlib inline
import matplotlib.pyplot as plt
f, axes = plt.subplots(nrows=3, sharey=True, sharex=True, figsize=(7, 5))
f.tight_layout()
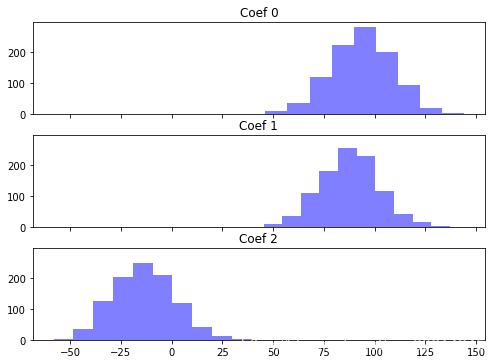
for i, ax in enumerate(axes):
ax.hist(coefs[:, i], color='b', alpha=.5)
ax.set_title("Coef {}".format(i))
return coefs
coefs = fit_2_regression(lr)
# 我们再用Ridge来拟合数据,对比结果:
from sklearn.linear_model import Ridge
coefs_r = fit_2_regression(Ridge())
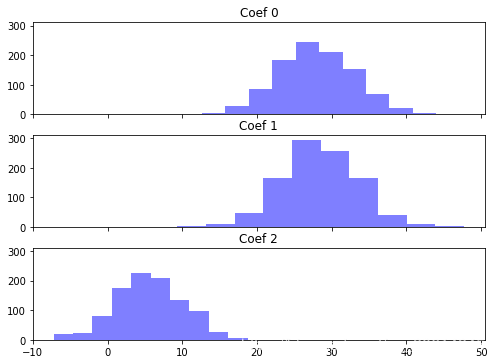
两个回归算法的结果看着好像差不多,其实不然。岭回归的相关系数更接近0。让我们看看两者相关系数的差异:
np.mean(coefs - coefs_r, axis=0)
# array([ 65.29814078, 59.2729781 , -19.31712032])
np.var(coefs, axis=0)
# array([233.05179112, 204.6986085 , 228.77835216])
np.var(coefs_r, axis=0)
# array([24.0402546 , 26.0985284 , 19.94299558])
从均值上看,线性回归比岭回归的相关系数要更很多。均值显示的差异其实是线性回归的相关系数隐含的偏差。
岭回归的相关系数方差也会小很多。这就是机器学习里著名的偏差-方差均衡(Bias-Variance Trade-off)。下一个主题我们将介绍如何调整岭回归的参数正则化,那是偏差-方差均衡的核心内容。
2.4 优化岭回归参数
当你使用岭回归模型进行建模时,需要考虑Ridge的alpha参数。
这是我们第一个进行模型参数优化的主题,通常用交叉检验(cross validation)完成。在后面的主题中,还会有更简便的方式实现这些,但是这里我们一步一步来实现岭回归的优化。
在scikit-learn里面,岭回归的参数就是RidgeRegression的alpha参数;因此,问题就是最优的alpha参数是什么。
from sklearn.datasets import make_regression
reg_data, reg_target = make_regression(n_samples=100,
n_features=2, effective_rank=1, noise=10)
在linear_models模块中,有一个对象叫RidgeCV,表示岭回归交叉检验(ridge cross-validation)。这个交叉检验类似于留一交叉验证法(leave-one-out cross-validation,LOOCV)。这种方法是指训练数据时留一个样本,测试的时候用这个未被训练过的样本.
import numpy as np
from sklearn.linear_model import RidgeCV
rcv = RidgeCV(alphas=np.array([.1, .2, .3, .4]))
rcv.fit(reg_data, reg_target)
rcv.alpha_
# 0.1
# 这里,0.1是最优参数,我们还想看到0.1附近更精确的值:
rcv = RidgeCV(alphas=np.array([.08, .09, .1, .11, .12]))
rcv.fit(reg_data, reg_target)
rcv.alpha_
# 0.08
在交叉检验的每一步里,模型的拟合效果都是用测试样本的误差表示。默认情况使用平方误差。我们可以让RidgeCV储存交叉检验的数据,这样就可以可视化整个过程:
alphas_to_test = np.linspace(0.0001, 0.05)
rcv3 = RidgeCV(alphas=alphas_to_test, store_cv_values=True)
rcv3.fit(reg_data, reg_target)
你会看到,我们测试了0.0001到0.05区间中的50个点。由于我们把store_cv_values设置成true,我们可以看到每一个值对应的拟合效果:
rcv3.cv_values_.shape
# (100, 50)
通过100个样本的回归数据集,我们获得了50个不同的alpha值。我们可以看到50个误差值,最小的均值误差对应最优的alpha值:
smallest_idx = rcv3.cv_values_.mean(axis=0).argmin()
alphas_to_test[smallest_idx]
# 0.027595918367346938
rcv3.alpha_
0.027595918367346938
通过可视化图形可以更直观的显示出来。我们画出50个测试alpha值的图:
%matplotlib inline
import matplotlib.pyplot as plt
f, ax = plt.subplots(figsize=(7, 5))
ax.set_title(r"Various values of $\alpha$")
xy = (alphas_to_test[smallest_idx],
rcv3.cv_values_.mean(axis=0)[smallest_idx])
xytext = (xy[0] + .01, xy[1] + .1)
ax.annotate(r'Chosen $\alpha$', xy=xy, xytext=xytext,
arrowprops=dict(facecolor='black', shrink=0, width=0)
)
ax.plot(alphas_to_test, rcv3.cv_values_.mean(axis=0));
如果我们想用其他误差自定义评分函数,也是可以实现的。前面我们介绍过MAD误差,我们可以用它来评分。首先我们需要定义损失函数:
def MAD(target, prediction):
absolute_deviation = np.abs(target - prediction)
return absolute_deviation.mean()
定义损失函数之后,我们用sklearn量度中的make_scorer函数来处理。这样做可以标准化自定义的函数,让scikit-learn对象可以使用它。另外,由于这是一个损失函数不是一个评分函数,是越低越好,所以要用sklearn来把最小化问题转化成最大化问题:
import sklearn
MAD = sklearn.metrics.make_scorer(MAD, greater_is_better=False)
rcv4 = RidgeCV(alphas=alphas_to_test, store_cv_values=True, scoring=MAD)
rcv4.fit(reg_data, reg_target)
smallest_idx = rcv4.cv_values_.mean(axis=0).argmin()
alphas_to_test[smallest_idx]
# 0.05
2.5 LASSO正则化
LASSO( least absolute shrinkage and selection operator,最小绝对值收缩和选择算子)方法与岭回归和LARS(least angle regression,最小角回归)很类似。与岭回归类似,它也是通过增加惩罚函数来判断、消除特征间的共线性。与LARS相似的是它也可以用作参数选择,通常得出一个相关系数的稀疏向量。
# 首先,我们还是用make_regression函数来建立数据集:
from sklearn.datasets import make_regression
reg_data, reg_target = make_regression(n_samples=200,
n_features=500, n_informative=5, noise=5)
# 之后,我们导入`lasso`对象:
from sklearn.linear_model import Lasso
lasso = Lasso()
lasso.fit(reg_data, reg_target)
# 再让我们看看还有多少相关系数非零:
import numpy as np
np.sum(lasso.coef_ != 0)
# 8
lasso_0 = Lasso(0)
lasso_0.fit(reg_data, reg_target)
np.sum(lasso_0.coef_ != 0)
# 500
# LASSO交叉检验
from sklearn.linear_model import LassoCV
lassocv = LassoCV()
lassocv.fit(reg_data, reg_target)
lassocv.alpha_
# 0.8357255768559891
# 计算的相关系数也可以看到:
lassocv.coef_[:5]
np.sum(lassocv.coef_ != 0)
# 12
LASSO特征选择
LASSO通常用来为其他方法做特征选择。例如,你可能会用LASSO回归获取适当的特征变量,然后在其他算法中使用。要获取想要的特征,需要创建一个非零相关系数的列向量,然后再其他算法拟合:
mask = lassocv.coef_ != 0
new_reg_data = reg_data[:, mask]
new_reg_data.shape
# (200, 12)
2.6 LARS正则化
LARS是一种回归手段,适用于解决高维问题,也就是p>>n的情况,其中p表示列或者特征变量,n表示样本数量。
# 首先让我们导入必要的对象。这里我们用的数据集是200个数据,500个特征。
# 我们还设置了一个低噪声,和少量提供信息的(informative)特征:
import numpy as np
from sklearn.datasets import make_regression
reg_data, reg_target = make_regression(n_samples=200,n_features=500,
n_informative=10, noise=2)
reg_data.shape, reg_target.shape
# ((200, 500), (200,))
由于我们用了10个信息特征,因此我们还要为LARS设置10个非0的相关系数。我们事先可能不知道信息特征的准确数量,但是出于试验的目的是可行的。
from sklearn.linear_model import Lars
lars = Lars(n_nonzero_coefs=10)
lars.fit(reg_data, reg_target)
# 我们可以检验一下看看LARS的非0相关系数的和:
np.sum(lars.coef_ != 0)
# 10
问题在于为什么少量的特征反而变得更加有效。要证明这一点,让我们用一半数量来训练两个LARS模型,一个用12个非零相关系数,另一个非零相关系数用默认值。这里用12个是因为我们对重要特征的数量有个估计,但是可能无法确定准确的数量:
train_n = 100
lars_12 = Lars(n_nonzero_coefs=12)
lars_12.fit(reg_data[:train_n], reg_target[:train_n])
lars_500 = Lars() #默认就是500
lars_500.fit(reg_data[:train_n], reg_target[:train_n])
np.mean(np.power(reg_target[train_n:] - lars.predict(reg_data[train_n:]), 2))
# 5.98715309047699
np.mean(np.power(reg_target[train_n:] - lars_12.predict(reg_data[train_n:]), 2))
# 53.48472292916442
np.mean(np.power(reg_target[train_n:] - lars_500.predict(reg_data[train_n:]), 2))
# 5.124946479008267e+32
测试集的误差明显高很多。高维数据集问题就在于此;通常面对大量的特征时,想找出一个对训练集拟合很好的模型并不难,但是拟合过度却是更大的问题。
LARS通过重复选择与残存变化相关的特征。从图上看,相关性实际上就是特征与残差之间的最小角度;这就是LARS名称的由来。选择第一个特征之后,LARS会继续沿着最小角的方向移动,直到另一个特征与残差有同样数量的相关性。然后,LARS会沿着两个特征组合的角度移动。如下图所示:
%matplotlib inline
import matplotlib.pyplot as plt
def unit(*args):
squared = map(lambda x: x**2, args)
distance = sum(squared) ** (.5)
return map(lambda x: x / distance, args)
f, ax = plt.subplots(nrows=3, figsize=(5, 10))
plt.tight_layout()
ax[0].set_ylim(0, 1.1)
ax[0].set_xlim(0, 1.1)
x, y = unit(1, 0.02)
ax[0].arrow(0, 0, x, y, edgecolor='black', facecolor='black')
ax[0].text(x + .05, y + .05, r"$x_1$")
x, y = unit(.5, 1)
ax[0].arrow(0, 0, x, y, edgecolor='black', facecolor='black')
ax[0].text(x + .05, y + .05, r"$x_2$")
x, y = unit(1, .45)
ax[0].arrow(0, 0, x, y, edgecolor='black', facecolor='black')
ax[0].text(x + .05, y + .05, r"$y$")
ax[0].set_title("No steps")
# step 1
ax[1].set_title("Step 1")
ax[1].set_ylim(0, 1.1)
ax[1].set_xlim(0, 1.1)
x, y = unit(1, 0.02)
ax[1].arrow(0, 0, x, y, edgecolor='black', facecolor='black')
ax[1].text(x + .05, y + .05, r"$x_1$")
x, y = unit(.5, 1)
ax[1].arrow(0, 0, x, y, edgecolor='black', facecolor='black')
ax[1].text(x + .05, y + .05, r"$x_2$")
x, y = unit(.5, 1)
ax[1].arrow(.5, 0.01, x, y, ls='dashed', edgecolor='black', facecolor='black')
ax[1].text(x + .5 + .05, y + .01 + .05, r"$x_2$")
ax[1].arrow(0, 0, .47, .01, width=.0015, edgecolor='black', facecolor='black')
ax[1].text(.47-.15, .01 + .03, "Step 1")
x, y = unit(1, .45)
ax[1].arrow(0, 0, x, y, edgecolor='black', facecolor='black')
ax[1].text(x + .05, y + .05, r"$y$")
# step 2
ax[2].set_title("Step 2")
ax[2].set_ylim(0, 1.1)
ax[2].set_xlim(0, 1.1)
x, y = unit(1, 0.02)
ax[2].arrow(0, 0, x, y, edgecolor='black', facecolor='black')
ax[2].text(x + .05, y + .05, r"$x_1$")
x, y = unit(.5, 1)
ax[2].arrow(0, 0, x, y, edgecolor='black', facecolor='black')
ax[2].text(x + .05, y + .05, r"$x_2$")
x, y = unit(.5, 1)
ax[2].arrow(.5, 0.01, x, y, ls='dashed', edgecolor='black', facecolor='black')
ax[2].text(x + .5 + .05, y + .01 + .05, r"$x_2$")
ax[2].arrow(0, 0, .47, .01, width=.0015, edgecolor='black', facecolor='black')
ax[2].text(.47-.15, .01 + .03, "Step 1")
## step 2
x, y = unit(1, .45)
ax[2].arrow(.5, .02, .4, .35, width=.0015, edgecolor='black', facecolor='black')
ax[2].text(x, y - .1, "Step 2")
x, y = unit(1, .45)
ax[2].arrow(0, 0, x, y, edgecolor='black', facecolor='black')
ax[2].text(x + .05, y + .05, r"$y$");
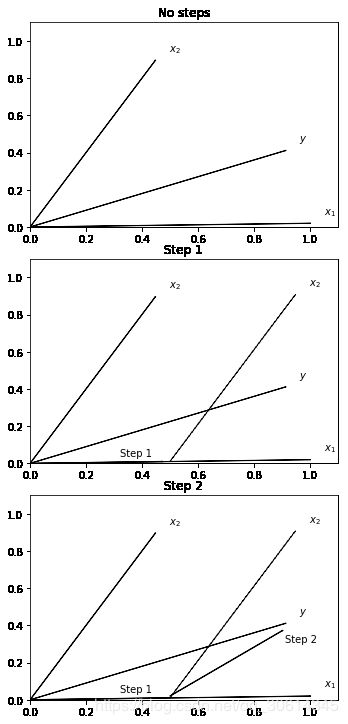
具体过程是,我们把 x 2 x2 x2沿着 x 1 x1 x1方向移动到一个位置: x 1 x1 x1与 y y y的点积与 x 1 x1 x1与 y y y的点积相同。到了这个位置之后,我们再沿着 x 1 x1 x1和 x 2 x2 x2夹角的一半的方向移动。
用交叉检验来优化领回归模型一样,我们可以对LARS做交叉检验:
from sklearn.linear_model import LarsCV
lcv = LarsCV()
lcv.fit(reg_data, reg_target)
# 用交叉检验可以帮助我们确定需要使用的非零相关系数的最佳数量。
np.sum(lcv.coef_ != 0)
# 10
2.7 用线性方法处理分类问题——逻辑回归
实际上线性模型也可以用于分类任务。方法是把一个线性模型拟合成某个类型的概率分布,然后用一个函数建立阈值来确定结果属于哪一类。
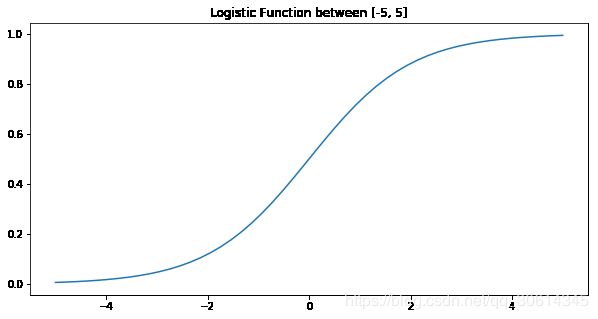
这里用的函数是经典的逻辑函数。一个非常简单的函数:
f ( x ) = 1 1 + e − t f(x)= \frac 1 {1+e^{-t}} f(x)=1+e−t1
它的图形如下图所示:
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
f, ax = plt.subplots(figsize=(10, 5))
rng = np.linspace(-5, 5)
log_f = np.apply_along_axis(lambda x:1 / (1 + np.exp(-x)), 0, rng)
ax.set_title("Logistic Function between [-5, 5]")
ax.plot(rng, log_f);
# 让我们用make_classification方法创建一个数据集来进行分类:
from sklearn.datasets import make_classification
X, y = make_classification(n_samples=1000, n_features=4)
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
X_train = X[:-200]
X_test = X[-200:]
y_train = y[:-200]
y_test = y[-200:]
lr.fit(X_train, y_train)
y_train_predictions = lr.predict(X_train)
y_test_predictions = lr.predict(X_test)
(y_train_predictions == y_train).sum().astype(float) / y_train.shape[0]
# 0.89
(y_test_predictions == y_test).sum().astype(float) / y_test.shape[0]
# 0.835
下面的内容你以后肯定会遇到。一种情况是一个类型与其他类型的权重不同(也就是正负样本的比例);例如,一个能可能权重很大,99%。这种情况在分类工作中经常遇到。经典案例就是信用卡虚假交易检测,大多数交易都不是虚假交易,但是不同类型误判的成本相差很大。
让我们建立一个分类问题,类型yy的不平衡权重95%,我们看看基本的逻辑回归模型如何处理这类问题:
X, y = make_classification(n_samples=5000, n_features=4, weights=[.95])
sum(y) / (len(y)*1.) #检查不平衡的类型
# 0.0536
X_train = X[:-500]
X_test = X[-500:]
y_train = y[:-500]
y_test = y[-500:]
lr.fit(X_train, y_train)
y_train_predictions = lr.predict(X_train)
y_test_predictions = lr.predict(X_test)
(y_train_predictions == y_train).sum().astype(float) / y_train.shape[0]
# 0.9817777777777777
(y_test_predictions == y_test).sum().astype(float) / y_test.shape[0]
# 0.976
结果看着还不错,但这是说如果我们把一个交易预测成正常交易(或者称为类型0),那么我们有95%左右的可能猜对。如果我们想看看模型对类型1的预测情况,可能就不是那么好了:
(y_test[y_test==1] == y_test_predictions[y_test==1]).sum().
astype(float) / y_test[y_test==1].shape[0]
# 0.7142857142857143
如果相比正常交易,我们更关心虚假交易;那么这是由商业规则决定的,我们可能会改变预测正确和预测错误的权重。
通常情况下,虚假交易与正常交易的权重与训练集的类型权重的倒数一致。但是,因为我们更关心虚假交易,所有让我们用多重采样(oversample)方法来表示虚假交易与正常交易的权重。
lr = LogisticRegression(class_weight={0: .15, 1: .85})
lr.fit(X_train, y_train)
y_train_predictions = lr.predict(X_train)
y_test_predictions = lr.predict(X_test)
(y_test[y_test==1] == y_test_predictions[y_test==1]).
sum().astype(float) / y_test[y_test==1].shape[0]
# 0.7857142857142857
(y_test_predictions == y_test).sum().astype(float) / y_test.shape[0]
# 0.968 准确率降低了
2.8 贝叶斯岭回归
岭回归和套索回归(lasso regression)用贝叶斯观点来解释,与频率优化观点解释相反。scikit-learn只实现了贝叶斯岭回归。
from sklearn.datasets import make_regression
X, y = make_regression(1000, 10, n_informative=2, noise=20)
from sklearn.linear_model import BayesianRidge
br = BayesianRidge()
有两组相关系数,分别是alpha_1 / alpha_2和lambda_1 / lambda_2。其中,alpha_*是先验概率分布的 α \alpha α超参数,lambda_*是先验概率分布的 λ \lambda λ超参数。
# 首先,让我们不调整参数直接拟合模型
br.fit(X, y)
br.coef_
br_alphas = BayesianRidge(alpha_1=10, lambda_1=10)
br_alphas.fit(X, y)
br_alphas.coef_
因为是贝叶斯岭回归,我们假设先验概率分布带有误差和 α \alpha α参数,先验概率分布都服从 Γ \Gamma Γ分布。
Γ \Gamma Γ分布是一种极具灵活性的分布。不同的形状参数和尺度参数的 Γ \Gamma Γ分布形状有差异。1e-06是 scikit-learn里面BayesianRidge形状参数的默认参数值。
import matplotlib.pyplot as plt
%matplotlib inline
from scipy.stats import gamma
import numpy as np
form = lambda x, y: "loc={}, scale={}".format(x, y)
g = lambda x, y=1e-06, z=1e-06: gamma.pdf(x, y, z)
g2 = lambda x, y=1e-06, z=1: gamma.pdf(x, y, z)
g3 = lambda x, y=1e-06, z=2: gamma.pdf(x, y, z)
rng = np.linspace(0, 5)
f, ax = plt.subplots(figsize=(8, 5))
ax.plot(rng, list(map(g, rng)), label=form(1e-06, 1e-06), color='r')
ax.plot(rng, list(map(g2, rng)), label=form(1e-06, 1), color='g')
ax.plot(rng, list(map(g3, rng)), label=form(1e-06, 2), color='b')
ax.set_title("Different Shapes of the Gamma Distribution")
ax.legend();
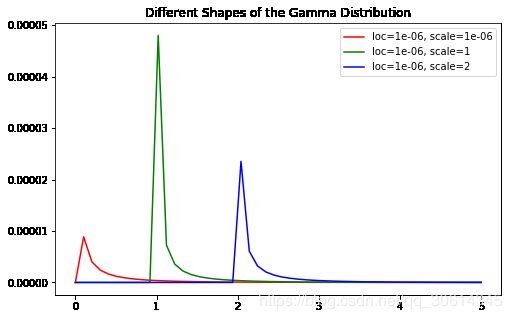
你会看到,相关系数最终都会收缩到0,尤其当形状参数特别小的时候。
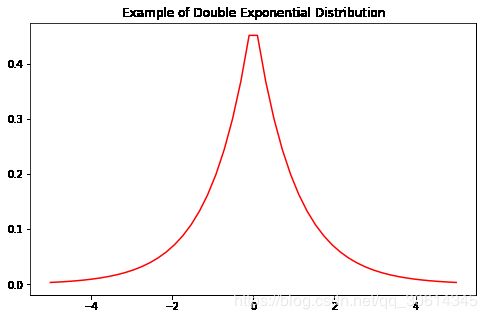
还有一种套索回归的贝叶斯解释。我们把先验概率分布看出是相关系数的函数;它们本身都是随机数。对于套索回归,我们选择一个可以产生0的分布,比如双指数分布(Double Exponential Distribution,也叫Laplace distribution)。
from scipy.stats import laplace
form = lambda x, y: "loc={}, scale={}".format(x, y)
g = lambda x: laplace.pdf(x)
rng = np.linspace(-5, 5)
f, ax = plt.subplots(figsize=(8, 5))
ax.plot(rng, list(map(g, rng)), color='r')
ax.set_title("Example of Double Exponential Distribution");
2.9 用梯度提升回归从误差中学习
梯度提升回归(Gradient boosting regression,GBR)是一种从它的错误中进行学习的技术。它本质上就是集思广益,集成一堆较差的学习算法进行学习。有两点需要注意:
- 每个学习算法准备率都不高,但是它们集成起来可以获得很好的准确率。
- 这些学习算法依次应用,也就是说每个学习算法都是在前一个学习算法的错误中学习
import numpy as np
from sklearn.datasets import make_regression
X, y = make_regression(1000, 2, noise=10)
from sklearn.ensemble import GradientBoostingRegressor as GBR
gbr = GBR()
gbr.fit(X, y)
gbr_preds = gbr.predict(X)
# 对比模型
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X, y)
lr_preds = lr.predict(X)
gbr_residuals = y - gbr_preds
lr_residuals = y - lr_preds
%matplotlib inline
from matplotlib import pyplot as plt
f, ax = plt.subplots(figsize=(7, 5))
f.tight_layout()
ax.hist(gbr_residuals,bins=20,label='GBR Residuals', color='b', alpha=.5);
ax.hist(lr_residuals,bins=20,label='LR Residuals', color='r', alpha=.5);
ax.set_title("GBR Residuals vs LR Residuals")
ax.legend(loc='best');
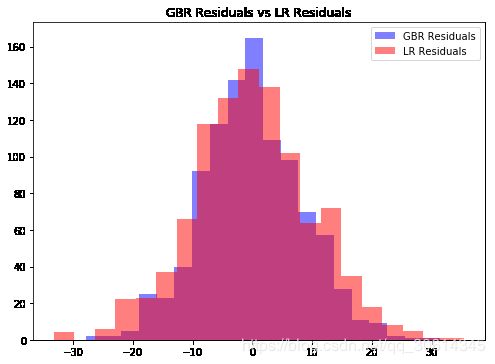
看起来好像GBR拟合的更好,但是并不明显。让我们用95%置信区间(Confidence interval,CI)对比一下:
np.percentile(gbr_residuals, [2.5, 97.5])
# array([-16.83708393, 16.22875202])
np.percentile(lr_residuals, [2.5, 97.5])
# array([-20.33516214, 19.84516844])
GBR的置信区间更小,数据更集中,因此其拟合效果更好;我们还可以对GBR算法进行一些调整来改善效果。我用下面的例子演示一下,然后在下一节介绍优化方法:
n_estimators = np.arange(100, 1100, 350)
gbrs = [GBR(n_estimators=n_estimator) for n_estimator in n_estimators]
residuals = {}
for i, gbr in enumerate(gbrs):
gbr.fit(X, y)
residuals[gbr.n_estimators] = y - gbr.predict(X)
f, ax = plt.subplots(figsize=(7, 5))
f.tight_layout()
colors = {800:'r', 450:'g', 100:'b'}
for k, v in residuals.items():
ax.hist(v,bins=20,label='n_estimators: %d' % k, color=colors[k], alpha=.5);
ax.set_title("Residuals at Various Numbers of Estimators")
ax.legend(loc='best');
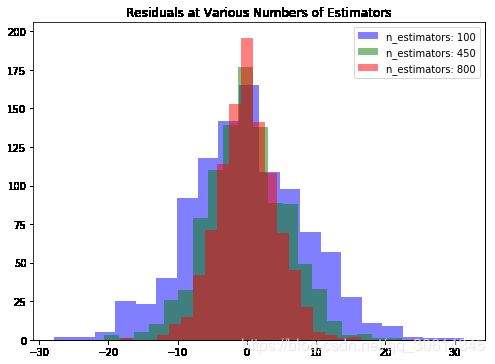
上面例子中GBR的第一个参数是n_estimators,指GBR使用的学习算法的数量。通常,如果你的设备性能更好,可以把n_estimators设置的更大,效果也会更好。还有另外几个参数要说明一下。
你应该在优化其他参数之前先调整max_depth参数。因为每个学习算法都是一颗决策树,max_depth决定了树生成的节点数。选择合适的节点数量可以更好的拟合数据,而更多的节点数可能造成拟合过度。
loss参数决定损失函数,也直接影响误差。ls是默认值,表示最小二乘法(least squares)。还有最小绝对值差值,Huber损失和分位数损失(quantiles)等等。
第三章 使用距离向量构建模型
本章包括以下主题:
- [使用 KMeans 对数据聚类]
- [优化形心数量]
- [评估聚类的正确性]
- [使用 MiniBatch KMeans 处理更多数据]
- [使用 KMeans 聚类来量化图像]
- [寻找特征空间中的最接近对象]
- [使用高斯混合模型的概率聚类]
- [将 KMeans 用于离群点检测]
- [将 KNN 用于回归]
3.1 使用 KMeans 对数据聚类
from sklearn.datasets import make_blobs
blobs, classes = make_blobs(500, centers=3)
import matplotlib.pyplot as plt
import numpy as np
f, ax = plt.subplots(figsize=(7.5, 7.5))
rgb = np.array(['r', 'g', 'b'])
ax.scatter(blobs[:, 0], blobs[:, 1], color=rgb[classes])
ax.set_title("Blobs")
plt.show()
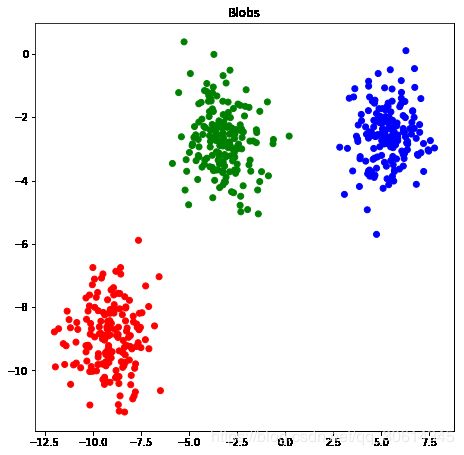
现在我们可以使用 KMeans 来寻找这些簇的形心。第一个例子中,我们假装知道有三个形心。
from sklearn.cluster import KMeans
kmean = KMeans(n_clusters=3)
kmean.fit(blobs)
kmean.cluster_centers_
f, ax = plt.subplots(figsize=(7.5, 7.5))
ax.scatter(blobs[:, 0], blobs[:, 1], color=rgb[classes])
ax.scatter(kmean.cluster_centers_[:, 0],
kmean.cluster_centers_[:, 1], marker='*', s=250,
color='black', label='Centers')
ax.set_title("Blobs")
ax.legend(loc='best')
plt.show()
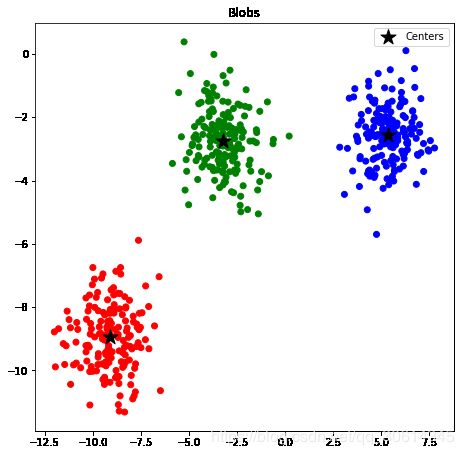
其它属性也很实用。例如,labels_属性会产生每个点的预期标签。
kmean.labels_[:5]
classes[:5]
# rtansform函数十分有用,它会输出每个点到形心的距离。
kmean.transform(blobs)[:5]
3.2 优化形心数量
形心难以解释,并且也难以判断是否数量正确。理解你的数据是否是未分类的十分重要,因为这会直接影响我们可用的评估手段。
from sklearn.datasets import make_blobs
import numpy as np
blobs, classes = make_blobs(500, centers=3)
from sklearn.cluster import KMeans
kmean = KMeans(n_clusters=3)
kmean.fit(blobs)
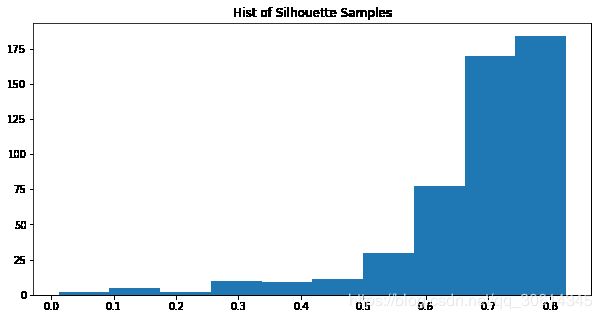
首先,我们查看轮廓(Silhouette)距离。轮廓距离是簇内不相似性、最近的簇间不相似性、以及这两个值最大值的比值。它可以看做簇间分离程度的度量。让我们看一看数据点到形心的距离分布,理解轮廓距离非常有用。
from sklearn import metrics
silhouette_samples = metrics.silhouette_samples(blobs,
kmean.labels_)
np.column_stack((classes[:5], silhouette_samples[:5]))
f, ax = plt.subplots(figsize=(10, 5))
ax.set_title("Hist of Silhouette Samples")
ax.hist(silhouette_samples)
plt.show()
轮廓系数的均值通常用于描述整个模型的拟合度。
silhouette_samples.mean()
# 0.6812179506374529
这十分普遍,事实上,metrics模块提供了一个函数来获得刚才的值。现在,让我们训练多个簇的模型,并看看平均得分是什么样:
# first new ground truth
blobs, classes = make_blobs(500, centers=10)
sillhouette_avgs = []
# this could take a while
for k in range(2, 60):
kmean = KMeans(n_clusters=k).fit(blobs)
sillhouette_avgs.append(metrics.silhouette_score(blobs,kmean.labels_))
f, ax = plt.subplots(figsize=(7, 5))
ax.plot(sillhouette_avgs)
plt.show()
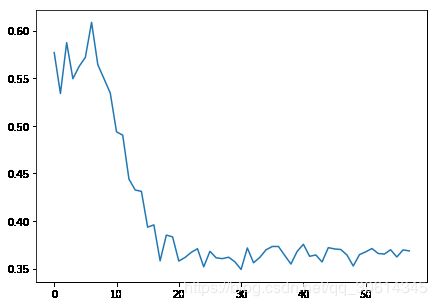
这个绘图表明,轮廓均值随着形心数量的变化情况。我们可以看到最优的数量是 3,根据所生成的数据。但是最优的数量看起来是 6 或者 7。这就是聚类的实际情况,十分普遍,我们不能获得正确的簇数量,我们只能估计簇数量的近似值。
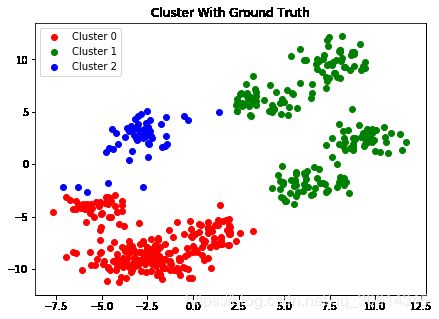
3.3 评估聚类的正确性
我们之前讨论了不知道真实情况的条件下的聚类评估。但是,我们还没有讨论簇已知条件下的 KMeans 评估。在许多情况下,这都是不可知的,但是如果存在外部的标注,我们就会知道真实情况,或者至少是代理。
from sklearn.cluster import KMeans
kmean = KMeans(n_clusters=3)
kmean.fit(blobs)
f, ax = plt.subplots(figsize=(7, 5))
colors = ['r', 'g', 'b']
ground_truth=kmean.labels_
for i in range(3):
p = blobs[ground_truth == i]
ax.scatter(p[:,0], p[:,1], c=colors[i],
label="Cluster {}".format(i))
ax.set_title("Cluster With Ground Truth")
ax.legend()
f.savefig("9485OS_03-16")
plt.show()
f, ax = plt.subplots(figsize=(7, 5))
colors = ['r', 'g', 'b']
for i in range(3):
p = blobs[ground_truth == i]
ax.scatter(p[:,0], p[:,1], c=colors[i],label="Cluster {}".format(i))
ax.scatter(kmean.cluster_centers_[:, 0],
kmean.cluster_centers_[:, 1], s=100,
color='black',
label='Centers')
ax.set_title("Cluster With Ground Truth")
ax.legend()
f.savefig("9485OS_03-17")
plt.show()
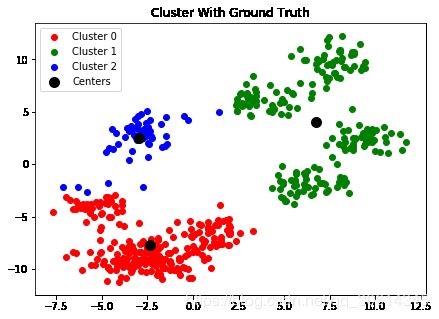
既然我们能够将聚类表现看做分类练习,在其语境中有用的方法在这里也有用:
for i in range(3):
print((kmean.labels_ == classes)[classes == i].astype(int).mean())
很显然我们有一些错乱的簇。所以让我们将其捋直,之后我们查看准确度。
new_ground_truth = classes.copy()
new_ground_truth[classes == 0] = 2
new_ground_truth[classes == 2] = 0
for i in range(3):
print((kmean.labels_ == new_ground_truth)[classes == i].astype(int).mean())
第二个相似性度量是互信息( mutual information score)得分。
from sklearn import metrics
metrics.normalized_mutual_info_score(classes, kmean.labels_)
# 0.6177336423149696
分数靠近 0,就说明标签的分配可能不是按照相似过程生成的。但是分数靠近 1,就说明两个标签有很强的一致性。
metrics.normalized_mutual_info_score(classes, classes)
# 1.0
metrics.mutual_info_score(classes, kmean.labels_)
# 0.9191046569854725
# 每个数据点和它所分配的簇的平方差之和
kmean.inertia_
# 7728.505035843488
3.4 使用 MiniBatch KMeans 处理更多数据
from sklearn.datasets import make_blobs
blobs, labels = make_blobs(int(1e6), 3)
print(blobs.shape)
from sklearn.cluster import KMeans, MiniBatchKMeans
kmeans = KMeans(n_clusters=3)
minibatch = MiniBatchKMeans(n_clusters=3)
%time kmeans.fit(blobs)
%time minibatch.fit(blobs)
# 聚类性能上的差异在下面展示:
kmeans.cluster_centers_[0]
minibatch.cluster_centers_[0]
# 我们可能要问的下一个问题就是,两个形心距离多远。
from sklearn.metrics import pairwise
pairwise.pairwise_distances(kmeans.cluster_centers_[0].reshape(1,-1),
minibatch.cluster_centers_[0].reshape(1,3))
# 看起来十分接近了。对角线包含形心的差异:
np.diag(pairwise.pairwise_distances(kmeans.cluster_centers_,
minibatch.cluster_centers_))
3.5 使用 KMeans 聚类来量化图像
目标是使用聚类来把图像变模糊
from scipy import ndimage
img = ndimage.imread("headshot.jpg")
plt.imshow(img)
plt.show()
img.shape
# (227, 227, 3)
x, y, z = img.shape
long_img = img.reshape(x*y, z)
long_img.shape
对点进行聚类来降低图像中的不同颜色的数量 – 这是一个简单的量化方式。
from sklearn import cluster
k_means = cluster.KMeans(n_clusters=5)
k_means.fit(long_img)
centers = k_means.cluster_centers_
centers
既然我们拥有了形心,我们需要的下一个东西就是标签。它会告诉我们,哪个点关联哪个簇。
labels = k_means.labels_
labels[:5]
pic=centers[labels].reshape(x, y, z)
pic.shape
plt.imshow(pic.astype(int))
plt.show()
3.6 寻找特征空间中的最接近对象
有时,最简单的事情就是求出两个对象之间的距离。我们刚好需要寻找一些距离的度量,计算成对(Pairwise)距离,并将结果与我们的预期比较。
Scikit-learn 中,有个叫做sklearn.metrics.pairwise的底层工具。它包含一些服务函数,计算矩阵X中向量之间的距离,或者X和Y中的向量距离。
我们会使用pairwise_distances函数来判断对象的接近程度。要记住,接近程度就像我们用于聚类/分类的距离函数。
from sklearn.metrics import pairwise
from sklearn.datasets import make_blobs
points, labels = make_blobs()
points.shape
# (100,100)
# 用于检查距离的最简单方式是pairwise_distances:
distances = pairwise.pairwise_distances(points)
distances.shape
# (100, 100)
# distances是个 NxN的矩阵,对角线为 0。在最简单的情况中,
# 让我们先看看每个点到第一个点的距离:
np.diag(distances) [:5]
# 现在我们可以查找最接近于第一个点的点:
distances[0][:5]
# 将点按照接近程度排序,很容易使用np.argsort做到:
ranks = np.argsort(distances[0])
ranks.shape
# (100,)
ranks[:5]
# array([ 0, 10, 61, 46, 42], dtype=int64)
points[ranks][:5]
给定一些距离函数,每个点都以成对函数来度量。通常为欧几里得距离,它是:
d ( x , y ) = ∑ t ( x i − y i ) 2 d(x, y)=\sqrt{\sum_{t}\left(x_{i}-y_{i}\right)^{2}} d(x,y)=∑t(xi−yi)2
def euclid_distances(x, y):
return np.power(np.power(x - y, 2).sum(), .5)
euclid_distances(points[0], points[1])
Scikit-learn 中存在一些其他函数,但是 Scikit-learn 也会使用 SciPy 的距离函数。Scikit-learn 距离函数支持稀疏矩阵。距离函数的更多信息请查看 SciPy 文档。
cityblockcosineeuclideanl1l2manhattan
我们现在可以解决问题了。例如,如果我们站在原点处的格子上,并且线是街道,为了到达点(5,5),我们需要走多远呢?
pairwise.pairwise_distances([[0, 0], [5, 5]], metric='cityblock')[0]
# array([ 0., 10.])
使用成对距离,我们可以发现位向量之间的相似性。这是汉明距离的事情,它定义为: ∑ i I x i ≠ y i \sum_{i} I_{x_{i} \neq y_{i}} ∑iIxi̸=yi
X = np.random.binomial(1, .5, size=(2, 4)).astype(np.bool)
pairwise.pairwise_distances(X, metric='hamming')
3.7 使用高斯混合模型的概率聚类
在 KMeans 中,我们假设簇的方差是相等的。这会导致空间的细分,这决定了簇如何被分配。但是,如果有一种场景,其中方差不是相等的,并且每个簇中的点拥有一个与之相关的概率,会怎么样?
有一种更加概率化的方式,用于查看 KMeans 聚类。KMeans 聚类相当于将协方差矩阵S应用于高斯混合模型,这个矩阵可以分解为单位矩阵成误差。对于每个簇,协方差结构是相同的。这就产生了球形聚类。
但是,如果我们允许S变化,就可以估计 GMM,并将其用于预测。我们会以单变量的角度看到它的原理,之后扩展为多个维度。
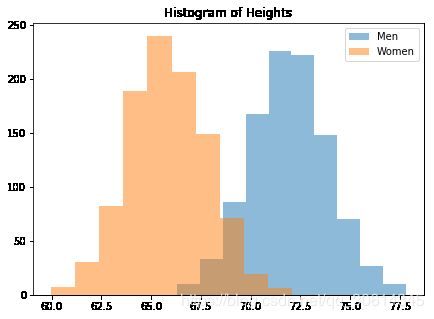
首先,我们需要创建一些数据。例如,让我们模拟女性和男性的身高。这是个简单的例子,但是会展示出我们在 N 维空间中想要完成的东西,这比较易于可视化:
import numpy as np
N = 1000
in_m = 72
in_w = 66
s_m = 2
s_w = s_m
m = np.random.normal(in_m, s_m, N)
w = np.random.normal(in_w, s_w, N)
from matplotlib import pyplot as plt
f, ax = plt.subplots(figsize=(7, 5))
ax.set_title("Histogram of Heights")
ax.hist(m, alpha=.5, label="Men");
ax.hist(w, alpha=.5, label="Women");
ax.legend()
plt.show()
w.shape,m.shape
# ((1000,), (1000,))
random_sample = np.random.choice([True, False], size=m.size)
m_test = m[random_sample]
m_train = m[~random_sample]
w_test = w[random_sample]
w_train = w[~random_sample]
# 现在我们需要获得男性和女性高度的经验分布,基于训练集:
from scipy import stats
m_pdf = stats.norm(m_train.mean(), m_train.std())
w_pdf = stats.norm(w_train.mean(), w_train.std())
# 对于测试集,我们要计算,基于数据点从每个分布中生成的概率,
# 并且最可能的分布会分配合适的标签。当然,我们会看到有多么准确。
m_pdf.pdf(m[0])
# 0.19978402252176347
w_pdf.pdf(m[0])
# 0.0018615006196173731
# 要注意概率中的差异。假设当男性的概率更高时,我们会猜测,
# 但是如果女性的概率更高,我们会覆盖它。
guesses_m = np.ones_like(m_test)
guesses_m[m_pdf.pdf(m_test) < w_pdf.pdf(m_test)] = 0
guesses_m.mean()
# 0.9343936381709742
guesses_w = np.ones_like(w_test)
guesses_w[m_pdf.pdf(w_test) > w_pdf.pdf(w_test)] = 0
guesses_w.mean()
# 0.952286282306163
# 让我们允许两组间的方差不同。首先,创建一些新的数组:
s_m = 1
s_w = 4
m = np.random.normal(in_m, s_m, N)
w = np.random.normal(in_w, s_w, N)
# 之后,创建训练集:
m_test = m[random_sample]
m_train = m[~random_sample]
w_test = w[random_sample]
w_train = w[~random_sample]
f, ax = plt.subplots(figsize=(7, 5))
ax.set_title("Histogram of Heights")
ax.hist(m_train, alpha=.5, label="Men");
ax.hist(w_train, alpha=.5, label="Women");
ax.legend()
plt.show()
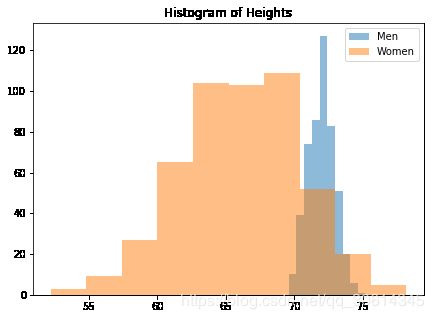
让我们看看男性和女性之间的方差差异:现在我们可以创建相同的 PDF:
m_pdf = stats.norm(m_train.mean(), m_train.std())
w_pdf = stats.norm(w_train.mean(), w_train.std())
你可以在多维空间中想象他:
class_A = np.random.normal(0, 1, size=(100, 2))
class_B = np.random.normal(4, 1.5, size=(100, 2))
f, ax = plt.subplots(figsize=(7, 5))
ax.scatter(class_A[:,0], class_A[:,1], label='A', c='r')
ax.scatter(class_B[:,0], class_B[:,1], label='B')
plt.show()
工作原理
from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(n_components=2)
X = np.row_stack((class_A, class_B))
y = np.hstack((np.ones(100), np.zeros(100)))
train = np.random.choice([True, False], 200)
gmm.fit(X[train])
gmm.predict(X[train])[:5]
f, ax = plt.subplots(figsize=(7, 5))
colors = ['r', 'g']
ground_truth=gmm.predict(X[train])
for i in range(2):
p = X[train][ground_truth == i]
ax.scatter(p[:,0], p[:,1], c=colors[i],
label="Cluster {}".format(i))
ax.set_title("Cluster With Ground Truth")
ax.legend()
plt.show()
3.8 将 KMeans 用于离群点检测
我们会查看 Kmeans 离群点检测的机制和正义。它对于隔离一些类型的错误很实用,但是使用时应多加小心。
我们会使用 KMeans,对簇中的点执行离群点检测。要注意,提及离群点和离群点检测时有很多“阵营”。以便面,我们可能通过移除离群点,来移除由数据生成过程生成的点。另一方面,离群点可能来源于测量误差或一些其它外部因素。
我们的假设是,我们移除离群点的选择是合理的。
离群点检测的操作是,查找簇的形心,之后通过点到形心的距离来识别潜在的离群点。
# 首先,我们会生成 100 个点的单个数据块,之后我们会识别 5 个离形心最远的点。
# 它们就是潜在的离群点。
from sklearn.datasets import make_blobs
X, labels = make_blobs(100, centers=1)
import numpy as np
# 非常重要的是,Kmeans 聚类只有一个形心。这个想法类似于用于离群点检测的单类 SVM。
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=1)
kmeans.fit(X)
f, ax = plt.subplots(figsize=(7, 5))
ax.set_title("Blob")
ax.scatter(X[:, 0], X[:, 1], label='Points')
ax.scatter(kmeans.cluster_centers_[:, 0],
kmeans.cluster_centers_[:, 1],
label='Centroid',
color='r')
ax.legend()
plt.show()
# 现在,让我们识别五个最接近的点:
distances = kmeans.transform(X)
# argsort returns an array of indexes which will
# sort the array in ascending order
# so we reverse it via [::-1] and take the top five with [:5]
sorted_idx = np.argsort(distances.ravel())[::-1][:5]
sorted_idx
# array([ 6, 97, 42, 8, 78], dtype=int64)
# 现在,让我们看看哪个点离得最远:
f, ax = plt.subplots(figsize=(7, 5))
ax.set_title("Single Cluster")
ax.scatter(X[:, 0], X[:, 1], label='Points')
ax.scatter(kmeans.cluster_centers_[:, 0],
kmeans.cluster_centers_[:, 1],
label='Centroid', color='r')
ax.scatter(X[sorted_idx][:, 0], X[sorted_idx][:, 1],
label='Extreme Value', edgecolors='g',
facecolors='none', s=100)
ax.legend(loc='best')
plt.show()
# 如果我们喜欢的话,移除这些点很容易。
new_X = np.delete(X, sorted_idx, axis=0)
# 同样,移除这些点之后,形心明显变化了。
new_kmeans = KMeans(n_clusters=1)
new_kmeans.fit(new_X)
# 让我们将旧的和新的形心可视化:
f, ax = plt.subplots(figsize=(7, 5))
ax.set_title("Extreme Values Removed")
ax.scatter(new_X[:, 0], new_X[:, 1], label='Pruned Points')
ax.scatter(kmeans.cluster_centers_[:, 0],
kmeans.cluster_centers_[:, 1], label='Old Centroid',
color='r', s=80, alpha=.5)
ax.scatter(new_kmeans.cluster_centers_[:, 0],
new_kmeans.cluster_centers_[:, 1], label='New Centroid',
color='m', s=80, alpha=.5)
ax.legend(loc='best')
plt.show()
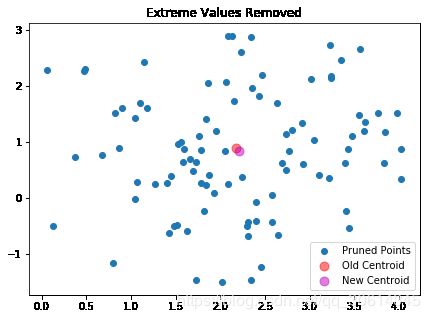
显然,形心没有移动多少,仅仅移除五个极端点时,我们的预期就是这样。这个过程可以重复,知道我们对数据表示满意。
高斯分布和 KMeans 聚类之间有本质联系。让我们基于形心和样本的协方差矩阵创建一个经验高斯分布,并且查看每个点的概率 – 理论上是我们溢出的五个点。这刚好展示了,我们实际上溢出了拥有最低可能性的值。
使用下列命令来创建经验高斯分布:
from scipy import stats
emp_dist = stats.multivariate_normal(
kmeans.cluster_centers_.ravel())
lowest_prob_idx = np.argsort(emp_dist.pdf(X))[:5]
lowest_prob_idx
# array([70, 4, 19, 83, 88], dtype=int64)
3.9 将 KNN 用于回归
对于 KNN 回归来说,我们使用特征空间中的 K 个最近点,来构建回归,而不像常规回归那样使用整个特征空间。
# 我们使用iris数据集:
from sklearn import datasets
iris = datasets.load_iris()
iris.feature_names
# 我们尝试基于萼片长度和宽度来预测花瓣长度。我们同时训练一个线性回归,
# 来对比观察 KNN 回归有多好。
X=iris.data[:,[0,1]]
y=iris.data[:,2]
X.shape,y.shape
# ((150, 2), (150,))
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X, y)
print("The MSE is: {:.2}".format(np.power(y - lr.predict(X),2).mean()) )
# The MSE is: 0.41
# 现在,对于 KNN 回归,使用下列代码:
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors=10)
knnr.fit(X, y)
print("The MSE is: {:.2}".format(np.power(y - knnr.predict(X),2).mean()))
# The MSE is: 0.17
# 让我们看看,当我们让它使用最接近的 10 个点用于回归时,KNN 回归会做什么?
f, ax = plt.subplots(nrows=2, figsize=(7, 10))
ax[0].set_title("Predictions")
ax[0].scatter(X[:, 0], X[:, 1], s=lr.predict(X)*80, label='LRPredictions',
color='c', edgecolors='black')
ax[1].scatter(X[:, 0], X[:, 1], s=knnr.predict(X)*80, label='k-NNPredictions',
color='m',
edgecolors='black')
ax[0].legend()
ax[1].legend()
plt.show()
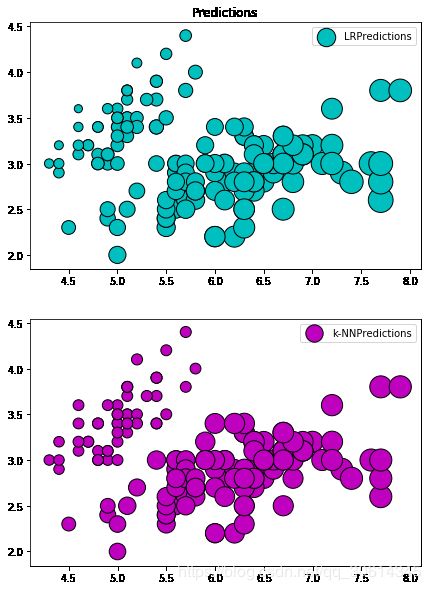
很显然,预测大部分都是接近的。但是让我们与实际情况相比,看看 Setosa 物种的预测:
setosa_idx = np.where(iris.target_names=='setosa')
print(setosa_idx)
setosa_mask = iris.target == setosa_idx[0]
print(setosa_mask)
print(y[setosa_mask][:5])
knnr.predict(X)[setosa_mask][:5]
lr.predict(X)[setosa_mask][:5]
example_point = X[0]
lr.predict(example_point.reshape(1,-1))
knnr.predict(example_point.reshape(1,-1))
现在,我们需要获取离我们的our_example_point最近的 10 个点:
from sklearn.metrics import pairwise
distances_to_example = pairwise.pairwise_distances(X)[0]
print(distances_to_example.shape)
ten_closest_points = X[np.argsort(distances_to_example)][:10]
ten_closest_y = y[np.argsort(distances_to_example)][:10]
ten_closest_y.mean()