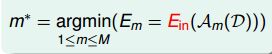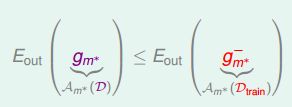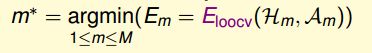名词:
(本节主要内容)Validation 验证,将数据集划分出测试集
Dval validation set 验证集
Dtrain 训练数据集
Leave-One-Out Cross Validation 留一法交叉验证
独立同分布(iid)
转自: https://blog.csdn.net/red_stone1/article/details/72834968
上节课我们主要讲了为了避免overfitting,可以使用regularization方法来解决。在之前的Ein上加上一个regularizer,生成Eaug,将其最小化,这样可以有效减少模型的复杂度,避免过拟合现象的发生。那么,机器学习领域还有许多选择,如何保证训练的模型具有良好的泛化能力?本节课将介绍一些概念和方法来解决这个选择性的问题。
一、Model Selection Problem
机器学习模型建立的过程中有许多选择,例如对于简单的二元分类问题,首先是算法A的选择,有PLA,pocket,linear regression,logistic regression等等;其次是迭代次数T的选择,有100,1000,10000等等;之后是学习速率η的选择,有1,0.01,0.0001等等;接着是模型特征转换Φ的选择,有linear,quadratic,poly-10,Legendre-poly-10等等;然后是正则化regularizer的选择,有L2,L1等等;最后是正则化系数λ的选择,有0,0.01,1等等。不同的选择搭配,有不同的机器学习效果。我们的目标就是找到最合适的选择搭配,得到一个好的矩g,构建最佳的机器学习模型。
假设有M个模型,对应有H1,H2,⋯,HM,即有M个hypothesis set,演算法为A1,A2,⋯,AM,共M个。我们的目标是从这M个hypothesis set中选择一个模型Hm∗,通过演算法Am∗对样本集D的训练,得到一个最好的矩gm∗,使其Eout(gm∗)最小。所以,问题的关键就是机器学习中如何选择到最好的矩gm∗。
考虑有这样一种方法,对M个模型分别计算使Ein最小的矩g,再横向比较,取其中能使Ein最小的模型的矩gm∗:
但是Ein足够小并不能表示模型好,反而可能表示训练的矩gm∗发生了过拟合,泛化能力很差。而且这种“模型选择+学习训练”的过程,它的VC Dimension是dVC(H1∪H2),模型复杂度增加。总的来说,泛化能力差,用Ein来选择模型是不好的。
另外一种方法,如果有这样一个独立于训练样本的测试集,将M个模型在测试集上进行测试,看一下Etest的大小,则选取Etest最小的模型作为最佳模型:
这种测试集验证的方法,根据finite-bin Hoffding不等式,可以得到:
Eout(gm∗)≤Etest(gm∗)+O(logMNtest‾‾‾‾‾‾√)
由上式可以看出,模型个数M越少,测试集数目越大,那么O(logMNtest‾‾‾‾‾√)越小,即Etest(gm∗)越接近于Eout(gm∗)。
下面比较一下之前讲的两种方法,第一种方法使用Ein作为判断基准,使用的数据集就是训练集D本身;第二种方法使用Etest作为判断基准,使用的是独立于训练集D之外的测试集。前者不仅使用D来训练不同的gm,而且又使用D来选择最好的gm∗,那么gm∗对未知数据并不一定泛化能力好。举个例子,这相当于老师用学生做过的练习题再来对学生进行考试,那么即使学生得到高分,也不能说明他的学习能力强。所以最小化Ein的方法并不科学。而后者使用的是独立于D的测试集,相当于新的考试题能更好地反映学生的真实水平,所以最小化Etest更加理想。
但是,我们拿到的一都是训练集D,测试集是拿不到的。所以,寻找一种折中的办法,我们可以使用已有的训练集D来创造一个验证集validation set,即从D中划出一部分Dval作为验证集。D另外的部分作为训练模型使用,Dval独立开来,用来测试各个模型的好坏,最小化Eval,从而选择最佳的gm∗。
二、Validation
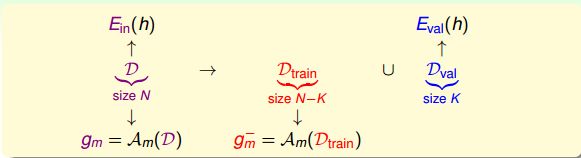
从训练集D中抽出一部分K个数据作为验证集Dval,Dval对应的error记为Eval。这样做的一个前提是保证Dval独立同分布(iid)于P(x,y),也就是说Dval的选择是从D中平均随机抽样得到的,这样能够把Eval与Eout联系起来。D中去除Dval后的数据就是供模型选择的训练数据Dtrain,其大小为N-k。从Dtrain中选择最好的矩,记为g−m。
假如D共有1000个样本,那么可以选择其中900个Dtrain,剩下的100个作为Dval。使用Dtrain训练模型,得到最佳的g−m,使用g−m对Dval进行验证,得到如下Hoffding不等式:
Eout(g−m)≤Eval(g−m)+O(logMK‾‾‾‾‾‾√)
假设有M种模型hypothesis set,Dval的数量为K,那么从每种模型m中得到一个在Dval上表现最好的矩,再横向比较,从M个矩中选择一个最好的m∗作为我们最终得到的模型。
现在由于数量为N的总样本D的一部分K作为验证集,那么只有N-k个样本可供训练。从Dtrain中得到最好的g−m∗,而总样本D对应的最好的矩为gm∗。根据之前的leraning curve很容易知道,训练样本越多,得到的模型越准确,其hypothesis越接近target function,即D的Eout比Dtrain的Eout要小:
所以,我们通常的做法是通过Dval来选择最好的矩g−m∗对应的模型m∗,再对整体样本集D使用该模型进行训练,最终得到最好的矩gm∗。
总结一下,使用验证集进行模型选择的整个过程为:先将D分成两个部分,一个是训练样本Dtrain,一个是验证集Dval。若有M个模型,那么分别对每个模型在Dtrain上进行训练,得到矩g−m,再用Dval对每个g−m进行验证,选择表现最好的矩g−m∗,则该矩对应的模型被选择。最后使用该模型对整个D进行训练,得到最终的gm∗。下图展示了整个模型选择的过程:
不等式关系满足:
Eout(gm∗)≤Eout(g−m∗)≤Eval(g−m∗)+O(logMK‾‾‾‾‾‾√)
下面我们举个例子来解释这种模型选择的方法的优越性,假设有两个模型:一个是5阶多项式HΦ5,一个是10阶多项式HΦ10。通过不使用验证集和使用验证集两种方法对模型选择结果进行比较,分析结果如下:
图中,横坐标表示验证集数量K,纵坐标表示Eout大小。黑色水平线表示没有验证集,完全使用Ein进行判断基准,那么HΦ10更好一些,但是这种方法的Eout比较大,而且与K无关。黑色虚线表示测试集非常接近实际数据,这是一种理想的情况,其Eout很小,同样也与K无关,实际中很难得到这条虚线。红色曲线表示使用验证集,但是最终选取的矩是g−m∗,其趋势是随着K的增加,它对应的Eout先减小再增大,当K大于一定值的时候,甚至会超过黑色水平线。蓝色曲线表示也使用验证集,最终选取的矩是gm∗,其趋势是随着K的增加,它对应的Eout先缓慢减小再缓慢增大,且一直位于红色曲线和黑色直线之下。从此可见,蓝色曲线对应的方法最好,符合我们之前讨论的使用验证集进行模型选择效果最好。这里提一点,当K大于一定的值时,红色曲线会超过黑色直线。这是因为随着K的增大,Dval增大,但可供模型训练的Dtrain在减小,那得到的g−m∗不具有很好的泛化能力,即对应的Eout会增大,甚至当K增大到一定值时,比Ein模型更差。那么,如何设置验证集K值的大小呢?根据之前的分析:
当K值很大时,Eval≈Eout,但是g−m与gm相差很大;当K值很小是,g−m≈gm,但是Eval与Eout可能相差很大。所以有个折中的办法,通常设置k=N5。值得一提的是,划分验证集,通常并不会增加整体时间复杂度,反而会减少,因为Dtrain减少了。
三、Leave-One-Out Cross Validation
假如考虑一个极端的例子,k=1,也就是说验证集大小为1,即每次只用一组数据对gm进行验证。这样做的优点是g−m≈gm,但是Eval与Eout可能相差很大。为了避免Eval与Eout相差很大,每次从D中取一组作为验证集,直到所有样本都作过验证集,共计算N次,最后对验证误差求平均,得到Eloocv(H,A),这种方法称之为留一法交叉验证,表达式为:
Eloocv(H,A)=1N∑n=1Nen=1N∑n=1Nerr(g−n(xn),yn)
这样求平均的目的是为了让Eloocv(H,A)尽可能地接近Eout(g)。
下面用一个例子图解留一法的过程:
如上图所示,要对二维平面上的三个点做拟合,上面三个图表示的是线性模型,下面三个图表示的是常数模型。对于两种模型,分别使用留一交叉验证法来计算Eloocv,计算过程都是每次将一个点作为验证集,其他两个点作为训练集,最终将得到的验证误差求平均值,就得到了Eloocv(linear)和Eloocv(constant),比较两个值的大小,取值小对应的模型即为最佳模型。
接下来,我们从理论上分析Leave-One-Out方法的可行性,即Eloocv(H,A)是否能保证Eout的矩足够好?假设有不同的数据集D,它的期望分布记为εD,则其Eloocv(H,A)可以通过推导,等于Eout(N−1)的平均值。由于N-1近似为N,Eout(N−1)的平均值也近似等于Eout(N)的平均值。具体推导过程如下:
最终我们得到的结论是Eloocv(H,A)的期望值和Eout(g−)的期望值是相近的,这代表得到了比较理想的Eout(g),Leave-One-Out方法是可行的。
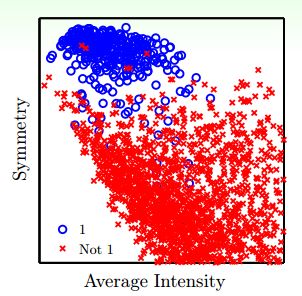
举一个例子,使用两个特征:Average Intensity和Symmetry加上这两个特征的非线性变换(例如高阶项)来进行手写数字识别。平面特征分布如下图所示:
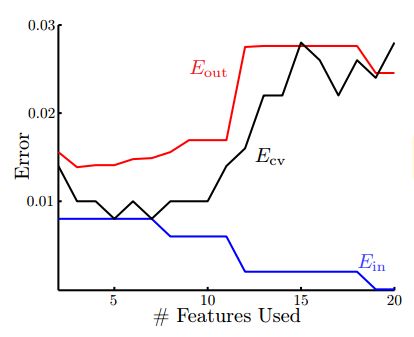
Error与特征数量的关系如下图所示:
从图中我们看出,随着特征数量的增加,Ein不断减小,Eout先减小再增大,虽然Ein是不断减小的,但是它与Eout的差距越来越大,发生了过拟合,泛化能力太差。而Ecv与Eout的分布基本一致,能较好地反映Eout的变化。所以,我们只要使用Leave-One-Out方法得到使Ecv最小的模型,就能保证其Eout足够小。下图是分别使用Ein和Eout进行训练得到的分类曲线:
很明显可以看出,使用Ein发生了过拟合,而Eloocv分类效果更好,泛化能力强。
四、V-Fold Cross Validation
接下来我们看看Leave-One-Out可能的问题是什么。首先,第一个问题是计算量,假设N=1000,那么就需要计算1000次的Eloocv,再计算其平均值。当N很大的时候,计算量是巨大的,很耗费时间。第二个问题是稳定性,例如对于二分类问题,取值只有0和1两种,预测本身存在不稳定的因素,那么对所有的Eloocv计算平均值可能会带来很大的数值跳动,稳定性不好。所以,这两个因素决定了Leave-One-Out方法在实际中并不常用。
针对Leave-One-Out的缺点,我们对其作出了改进。Leave-One-Out是将N个数据分成N分,那么改进措施是将N个数据分成V份(例如V=10),计算过程与Leave-One-Out相似。这样可以减少总的计算量,又能进行交叉验证,得到最好的矩,这种方法称为V-折交叉验证。其实Leave-One-Out就是V-折交叉验证的一个极端例子。
Ecv(H,A)=1V∑v=1VE(V)val(g−V)
所以呢,一般的Validation使用V-折交叉验证来选择最佳的模型。值得一提的是Validation的数据来源也是样本集中的,所以并不能保证交叉验证的效果好,它的模型一定好。只有样本数据越多,越广泛,那么Validation的结果越可信,其选择的模型泛化能力越强。
五、总结
本节课主要介绍了Validation验证。先从如何选择一个好的模型开始切入,例如使用Ein、Etest都是不太好的,最终使用Eval来进行模型选择。然后详细介绍了Validation的过程。最后,介绍了Leave-One-Out和V-Fold Cross两种验证方法,比较它们各自的优点和缺点,实际情况下,V-Fold Cross更加常用。