TreeMap全面解析(包含红黑树插入删除)
文章目录
- 一、红黑树插入与删除
- 1、规则
- 2、插入原则
- 3、删除原则(引用其他博客,作为自己理解)
- 4、AVL平衡二叉树LL、LR、RR、RL选择规则
- 二、TreeMap
- 1、属性
- 2、构造方法
- 3、内部类
- 4、核心方法
- 4、遍历方式
- 三、引用
一、红黑树插入与删除
1、规则
1、每个节点都只能是红色或者黑色
2、根节点是黑色
3、每个叶节点(NIL节点,空节点)是黑色的。
4、如果一个结点是红的,则它两个子节点都是黑的。也就是说在一条路径上不能出现相邻的两个红色结点。
5、从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
2、插入原则
1、插入节点总是红色
2、插入节点父节点为黑色,则不影响
3、插入节点父节点为红色,需要左右旋转调整
插入策略
1、根节点:插入黑节点
2、父节点为黑节点,插入红街店
3、父节点为红节点,叔父节点为红节点:此时插入当前节点就会导致出现两个红节点,破坏规则四,此时父亲、叔父节点都变为黑,而祖父节点变为红,祖父节点可能破坏规则四,出现两个红的情况,则继续递归
4、父节点为红,叔父节点为黑或者缺少,新增节点为右节点:先进行左旋转翻转成5的情况
5、父节点为红,叔父节点为黑或者缺少,新增节点为左节点:先以父节点右旋转,之后父节点与交换后的右节点交换颜色
之后按照其他规则调整(参考博客中在出现转换后情况使用规则3)
插入都可以按照这五个规则调整
插入图片参考博客:https://www.cnblogs.com/chenssy/p/3746600.html
3、删除原则(引用其他博客,作为自己理解)
引用博客:https://www.cnblogs.com/qingergege/p/7351659.html
删除节点类型:
1、删除叶子结点
2、删除节点只有左子树或者只有右子树
3、删除节点具有左右子树(找到直接后继节点,替换后删除后继节点,转换为1、2两种情况
- 删除节点为红色
情况1:删除红色叶子结点:直接删除就可以
情况2:删除红色节点只具有左子树或者只具有右子树:不可能出现
- 删除节点为黑色
情况1:删除的黑色节点只具有左子树或者只具有右子树
只能出现左子树为红或者右子树为红两种情况,其余情况不满足性质4
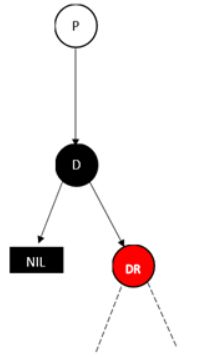
只需要用左或者右孩子替换删除节点,将替换节点修改为黑色
情况2:删除的黑色叶子结点
2.1 待删除节点的兄弟节点为红色
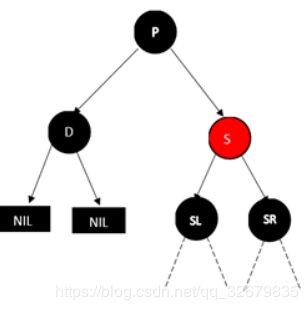
将父亲节点和兄弟节点的颜色互换,然后将P树进行AVL树种的RR(或者LL)型操作(转换为情况4:父亲节点为红色)
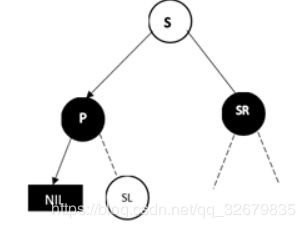
2.2 兄弟节点为黑色,且远侄子节点为红色。
D为左孩子对的情况,这时D的远侄子节点为S的右孩子

调整过程为,将P和S的颜色对调,然后对P树进行类似AVL树RR(或者LL)型的操作,最后把SR节点变成黑色,并删除D
2.3:兄弟节点S为黑色,远侄子节点为黑色,近侄子节点为红色
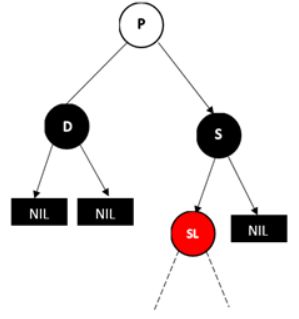
将sl右旋,交换S和SL的颜色,情况变为2

2.4:父亲节p为红色,兄弟节点和兄弟节点的两个孩子(只能是NULL节点)都为黑色的情况。
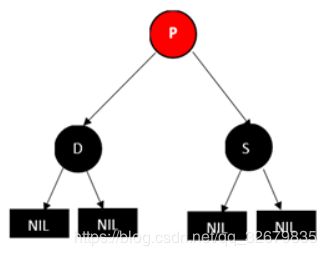
将父亲节点P改成黑色,将兄弟节点S改成红色,然后删除D
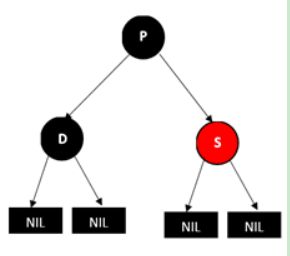
2.5:父亲节点p,兄弟节点s和兄弟节点的两个孩子(只能为NULL节点)都为黑色的情况

将兄弟节点S的颜色改成红色,这样删除D后P的左右两支的黑节点数就相等了,但是经过P的路径上的黑色节点数会少1,这个时候,我们再以P为起始点,继续根据情况进行平衡操作(这句话的意思就是把P当成D(只是不要再删除P了),再看是那种情况,再进行对应的调整,这样一直向上,直到新的起始点为根节点)
4、AVL平衡二叉树LL、LR、RR、RL选择规则
1、RX还是LX只需要观察左右子树的高度,如果左子树高度大于右字数高度,则LX,否则RX
2、之后判断X=R还是L
(1)如果RX,则比较插入值小于右子树,则RL;大于右子树则RR
(2)如果LX,则比较插入值小于左子树,则LL;大于右子树则LR
参考博客:https://www.cnblogs.com/qingergege/p/7294892.html
二、TreeMap
继承自AbstractMap和NavigableMap,保证了它对排序键值对的敏感度,底层是红黑树实现的。基本操作 containsKey、get、put 和 remove 的时间复杂度是 log(n) 。
另外,TreeMap是非同步的。 它的iterator 方法返回的迭代器是fail-fastl的。
1、属性
2、构造方法
记得继承SortedMap建议实现的四个构造方法吗?在源码中作者表达了这四个方法:
1、空构造函数
public TreeMap() {
comparator = null;
}
2、传入比较器
public TreeMap(Comparator comparator) {
this.comparator = comparator;
}
3、传入Map集合
public TreeMap(Map m) {
comparator = null;
putAll(m);
}
4、传入SotedMap集合
public TreeMap(SortedMap m) {
comparator = m.comparator();
try {
buildFromSorted(m.size(), m.entrySet().iterator(), null, null);//根据传入集合构造TreeMap
} catch (java.io.IOException cannotHappen) {
} catch (ClassNotFoundException cannotHappen) {
}
}
3、内部类
- NavigableSubMap:找到TreeMap中的subMap(子Map):比如在某个范围内的Map实现了公共操作
NavigableSubMap两个子类:(通过封装继承类的方式实现抽象方法)
1、AscendingSubMap:正序subMap
2、DescendingSubMap:逆序subMap
// lo是“子Map范围的最小值”,hi是“子Map范围的最大值”;
// loInclusive是“是否包含lo的标记”,hiInclusive是“是否包含hi的标记”
// fromStart是“表示是否从第一个节点开始计算”,
// toEnd是“表示是否计算到最后一个节点 ”
final K lo, hi;
final boolean fromStart, toEnd;
final boolean loInclusive, hiInclusive;
//省略
//以下方法需要子类去实现,因为subMap是顺序还是逆序不一定,因此这个方法需要子类实现
abstract TreeMap.Entry subLowest();
abstract TreeMap.Entry subHighest();
abstract TreeMap.Entry subCeiling(K key);
abstract TreeMap.Entry subHigher(K key);
abstract TreeMap.Entry subFloor(K key);
abstract TreeMap.Entry subLower(K key);
//key值正序迭代
abstract Iterator keyIterator();
abstract Spliterator keySpliterator();
//key值逆序迭代
abstract Iterator descendingKeyIterator();
4、核心方法
1、buildFromSorted方法
//将Map中的元素逐个添加到Treemap中,并返回map的中间元素作为根节点。二分法思路
private final Entry buildFromSorted(int level, int lo, int hi,
int redLevel,
Iterator it,
java.io.ObjectInputStream str,
V defaultVal)
throws java.io.IOException, ClassNotFoundException {
if (hi < lo) return null;
int mid = (lo + hi) >>> 1;
Entry left = null;
// 若lo小于mid,则递归调用获取(middel的)左孩子。
if (lo < mid)
left = buildFromSorted(level+1, lo, mid - 1, redLevel,
it, str, defaultVal);
// 从迭代器中获取键、值
K key;
V value;
if (it != null) {
if (defaultVal==null) {
Map.Entry entry = (Map.Entry)it.next();
key = (K)entry.getKey();
value = (V)entry.getValue();
} else {
key = (K)it.next();
value = defaultVal;
}
} else { // 流获取方式
key = (K) str.readObject();
value = (defaultVal != null ? defaultVal : (V) str.readObject());
}
Entry middle = new Entry<>(key, value, null);
// 若当前节点的深度=红色节点的深度,则将节点着色为红色。(不太理解)
if (level == redLevel)
middle.color = RED;
// 设置middle为left的父亲,left为middle的左孩子
if (left != null) {
middle.left = left;
left.parent = middle;
}
if (mid < hi) {
// 递归调用获取(middel的)右孩子。
Entry right = buildFromSorted(level+1, mid+1, hi, redLevel,
it, str, defaultVal);
// 设置middle为left的父亲,left为middle的左孩子
middle.right = right;
right.parent = middle;
}
return middle;
}
2、TreeMap的 firstEntry()、 lastEntry()、 lowerEntry()、 higherEntry()、 floorEntry()、 ceilingEntry()、 pollFirstEntry() 、 pollLastEntry() 类似,说明一下firstEntry
public Map.Entry firstEntry() {
return exportEntry(getFirstEntry());
}
//找到最左边的节点,就是最小的键值对实体
final Entry getFirstEntry() {
Entry p = root;
if (p != null)
while (p.left != null)
p = p.left;
return p;
}
// 之后需要通过exportEntry包装
static Map.Entry exportEntry(TreeMap.Entry e) {
return (e == null) ? null :
new AbstractMap.SimpleImmutableEntry<>(e);
}
SimpleImmutableEntry跃初视线,该类的实现是为了什么?源码中也就是通过迭代器获取键值,好像与Map集合获取没什么差别,那么需要去关注setValue这个函数,有没有发现调用这个函数的时候它会抛异常,因为firstEntry() 是对外接口; getFirstEntry() 是内部接口。目的是:防止用户修改返回的Entry。getFirstEntry()返回的Entry是可以被修改的,但是经过firstEntry()返回的Entry不能被修改,只可以读取Entry的key值和value值。
1、对firstEntry()返回的Entry对象只能进行getKey()、getValue()等读取操作;
2、getFirstEntry()返回的对象除了可以进行读取操作之后,还可以通过setValue()修改值。
public V setValue(V value) {
throw new UnsupportedOperationException();
}
3、TreeMap的firstKey()、lastKey()、lowerKey()、higherKey()、floorKey()、ceilingKey()原理都是类似的;介绍ceilingKey(找到大于等于该key的最小值):
public K ceilingKey(K key) {
return keyOrNull(getCeilingEntry(key));
}
static K keyOrNull(TreeMap.Entry e) {
return e == null? null : e.key;//没有获得则返回null
}
//获取key值
final Entry getCeilingEntry(K key) {
Entry p = root;
while (p != null) {
int cmp = compare(key, p.key);
//key值 0) {//key>p.key
if (p.right != null) {
p = p.right;//一直找右节点,起码得找一个比key值大的
} else {
//返回的 “p的后继节点”有2种可能性:第一,null;第二,TreeMap中大于key的最小的节点。
//null表示找到父节点了,再没有后继节点(跟获取中序遍历二叉树中某个节点的下一个节点比较类似),另一种就是找到大于key的最小的节点。
Entry parent = p.parent;
Entry ch = p;
while (parent != null && ch == parent.right) {
ch = parent;
parent = parent.parent;
}
return parent;
}
} else//等于key值
return p;
}
return null;
}
- **put()**真正涉及到红黑树的增加
public V put(K key, V value) {
Entry t = root;
//红黑树为根节点
if (t == null) {
compare(key, key); // type (and possibly null) check
root = new Entry<>(key, value, null);
size = 1;
modCount++;
return null;
}
int cmp;
Entry parent;
// 自定义比较器
Comparator cpr = comparator;
if (cpr != null) {
do {
parent = t;
cmp = cpr.compare(key, t.key);
if (cmp < 0)//key 0)//key>t.key找到右子树
t = t.right;
else
return t.setValue(value);//替换旧值
} while (t != null);
}
else {
if (key == null)
throw new NullPointerException();
@SuppressWarnings("unchecked")
Comparable k = (Comparable) key;//自然排序
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0)
t = t.left;//左孩子
else if (cmp > 0)
t = t.right;//右孩子
else
return t.setValue(value);
} while (t != null);
}
Entry e = new Entry<>(key, value, parent);//创建新的实体
if (cmp < 0)
parent.left = e;
else
parent.right = e;
fixAfterInsertion(e);//插入节点后调整节点
size++;
modCount++;
return null;
}
调整节点:
插入策略
1、根节点:插入黑节点
2、父节点为黑节点,插入红街店
3、父节点为红节点,叔父节点为红节点:此时插入当前节点就会导致出现两个红节点,破坏规则四,此时父亲、叔父节点都变为黑,而祖父节点变为红,祖父节点可能破坏规则四,出现两个红的情况,则继续递归
4、父节点为红,叔父节点为黑或者缺少,新增节点为右节点:先进行左旋转翻转成5的情况
5、父节点为红,叔父节点为黑或者缺少,新增节点为左节点:先以父节点右旋转,之后父节点与交换后的右节点交换颜色
之后按照其他规则调整(参考博客中在出现转换后情况使用规则3)
插入都可以按照这五个规则调整
插入图片参考博客:https://www.cnblogs.com/chenssy/p/3746600.html
private void fixAfterInsertion(Entry x) {
x.color = RED;//插入节点的颜色一定为红色
//情形1: 新节点x 是树的根节点,没有父节点不需要任何操作
//情形2: 新节点x 的父节点颜色是黑色的,也不需要任何操作
while (x != null && x != root && x.parent.color == RED) {
//父节点为红色,则需要调整(情况3)
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {//x节点的父节点属于左孩子
Entry y = rightOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {//叔父节点为红色
//父节点与叔父节点设置为黑色,
setColor(parentOf(x), BLACK);
setColor(y, BLACK);
setColor(parentOf(parentOf(x)), RED);//祖父节点设置为红色
x = parentOf(parentOf(x));//向上遍历,因为祖父节点也有可能会导致两个红色节点,破坏规则4
} else {//叔父节点为黑色或者是缺少
if (x == rightOf(parentOf(x))) {//如果x节点是父节点的有孩子
x = parentOf(x);
rotateLeft(x);//首先左翻转,变为情况5
}
//x节点是父节点的左孩子,直接进入情况5
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);//祖父节点与右节点交换颜色
rotateRight(parentOf(parentOf(x)));//父节点右旋转
}
} else {
//另外一种完全对称的情况
Entry y = leftOf(parentOf(parentOf(x)));//父节点是由孩子,叔父节点是左孩子
if (colorOf(y) == RED) {//叔父节点是红色
setColor(parentOf(x), BLACK);
setColor(y, BLACK);//父节点叔父节点设置为黑色
setColor(parentOf(parentOf(x)), RED);//父节点设置为红色
x = parentOf(parentOf(x));//遍历设置
} else {
if (x == leftOf(parentOf(x))) {//x是父节点的左节点
x = parentOf(x);
rotateRight(x);//右旋转,进入情况5
}
//直接是父节点的右孩子,进入情况5
setColor(parentOf(x), BLACK);
setColor(parentOf(parentOf(x)), RED);//祖父节点与左孩子交换颜色
rotateLeft(parentOf(parentOf(x)));//左旋转
}
}
}
root.color = BLACK;
}
- remove真正涉及到红黑树删除
public V remove(Object key) {
//获取Entry
Entry p = getEntry(key);
if (p == null)
return null;
V oldValue = p.value;
//删除的关键方法
deleteEntry(p);
return oldValue;
}
//查找t的后继结点
static TreeMap.Entry successor(Entry t) {
if (t == null)
return null;
//从t的右子树中找到最小的
else if (t.right != null) {
Entry p = t.right;
while (p.left != null)
p = p.left;
return p;
//当右子树为空时,向上找到第一个左父节点
} else {
Entry p = t.parent;
Entry ch = t;
while (p != null && ch == p.right) {
ch = p;
p = p.parent;
}
return p;
}
}
private void deleteEntry(Entry p) {
modCount++;
size--;
//① p的左右子树都不为空,找到右子树中最小的结点,将key、value赋给p,然后p指向后继结点
if (p.left != null && p.right != null) {
Entry s = successor(p);
p.key = s.key;
p.value = s.value;
p = s;
}
//获取p中不为空的结点,也可能两个都是空的
Entry replacement = (p.left != null ? p.left : p.right);
//① 替换的结点有一个子节点
if (replacement != null) {
replacement.parent = p.parent;
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)//替换节点具有左子树或者右子树,需要将左右子树连入原来的数中
p.parent.left = replacement;
else
p.parent.right = replacement;
//清空链接,以便可以使用fixAfterDeletion和内存回收
p.left = p.right = p.parent = null;
if (p.color == BLACK)//如果删除的节点是黑色,就会破坏规则5,需要重新调整
fixAfterDeletion(replacement);
// ② 删除的结点是根结点
} else if (p.parent == null) {
root = null;
// ③ 替换的结点是空节点
} else {
if (p.color == BLACK)
fixAfterDeletion(p);
if (p.parent != null) {
if (p == p.parent.left)
//清空链接,方便GC
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
//清空链接,方便GC
p.parent = null;
}
}
}
接下来是remove真正的调整阶段:
private void fixAfterDeletion(Entry x) {
while (x != root && colorOf(x) == BLACK) {
if (x == leftOf(parentOf(x))) {//x是左节点并且为黑色
Entry sib = rightOf(parentOf(x));
if (colorOf(sib) == RED) {//判断兄弟节点是否为红色
setColor(sib, BLACK);
setColor(parentOf(x), RED);//兄弟节点与父节点交换颜色
rotateLeft(parentOf(x));//左旋转
sib = rightOf(parentOf(x));//旋转后重新设置兄弟节点,就变为父节点为红色的情况
}
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {//远侄子和近侄子都为黑色
setColor(sib, RED);//兄弟节点设置为红色
x = parentOf(x);
} else {
if (colorOf(rightOf(sib)) == BLACK) {//兄弟节点的右节点为黑
setColor(leftOf(sib), BLACK);//左节点设置为黑
setColor(sib, RED);//兄弟节点设置为红色
rotateRight(sib);//右旋转后会出现远侄子节点为红色的情况
sib = rightOf(parentOf(x));
}
//远侄子节点为红色的情况
//主要目的就是将远侄子节点设置为黑色,通过左旋转,使得黑色平衡
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(rightOf(sib), BLACK);
rotateLeft(parentOf(x));
x = root;
}
} else { //对称求法
Entry sib = leftOf(parentOf(x));//兄弟节点是左孩子
//兄弟节点为红色的情况,父节点与兄弟节点交换颜色,之后就转换为父节点为红色的情况
if (colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf(x), RED);
rotateRight(parentOf(x));
sib = leftOf(parentOf(x));
}
//兄弟节点左右子节点都为黑
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED);//转变为兄弟节点为红色
x = parentOf(x);
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf(x));//转化为远侄子为红色的情况
}
//远侄子节点为红色的情况
//主要目的就是将远侄子节点设置为黑色,通过左旋转,使得黑色平衡
setColor(sib, colorOf(parentOf(x)));
setColor(parentOf(x), BLACK);
setColor(leftOf(sib), BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
setColor(x, BLACK);
}
4、遍历方式
1、keySet获取键的集合:返回Set
public Set keySet() {
return navigableKeySet();
}
public NavigableSet navigableKeySet() {
KeySet nks = navigableKeySet;
return (nks != null) ? nks : (navigableKeySet = new KeySet<>(this));//新建了一个KeySet类对象,传入当前Map
}
//现在看一下内部类就会发现,KeySet内部类提供了两种迭代方法,分别是正序迭代和逆序迭代
static final class KeySet extends AbstractSet implements NavigableSet {
private final NavigableMap m;
KeySet(NavigableMap map) { m = map; }
public Iterator iterator() {
if (m instanceof TreeMap)
return ((TreeMap)m).keyIterator();
else
return ((TreeMap.NavigableSubMap)m).keyIterator();//使用KeyIterator
}
public Iterator descendingIterator() {
if (m instanceof TreeMap)
return ((TreeMap)m).descendingKeyIterator();
else
return ((TreeMap.NavigableSubMap)m).descendingKeyIterator();
}
public int size() { return m.size(); }
public boolean isEmpty() { return m.isEmpty(); }
public boolean contains(Object o) { return m.containsKey(o); }
public void clear() { m.clear(); }
public E lower(E e) { return m.lowerKey(e); }//还是对已经实现的方法的封装
public E floor(E e) { return m.floorKey(e); }
public E ceiling(E e) { return m.ceilingKey(e); }
public E higher(E e) { return m.higherKey(e); }
public E first() { return m.firstKey(); }
public E last() { return m.lastKey(); }
public Comparator comparator() { return m.comparator(); }
public E pollFirst() {
Map.Entry e = m.pollFirstEntry();
return (e == null) ? null : e.getKey();
}
//其余省略
2、values()获取值的集合:返回Collection
public Collection values() {
Collection vs = values;
if (vs == null) {
vs = new Values();//新建Values类
values = vs;
}
return vs;
}
//继承自AbstractCOllection,通过ValueIterator获取值
class Values extends AbstractCollection {
public Iterator iterator() {
return new ValueIterator(getFirstEntry());
}
//省略
}
3、entrySet():获取键值对:返回set
public Set> entrySet() {
EntrySet es = entrySet;
return (es != null) ? es : (entrySet = new EntrySet());//新建EntrySet类
}
class EntrySet extends AbstractSet> {
public Iterator> iterator() {
return new EntryIterator(getFirstEntry());//通过EntryIterator迭代器获取
}
//省略
三、引用
【1】二叉树插入与删除:https://www.cnblogs.com/warehouse/p/9346757.html
【2】TreeMap相关源码:https://www.cnblogs.com/skywang12345/p/3310928.html#a5
【3】红黑树删除图解:https://www.cnblogs.com/qingergege/p/7351659.html
【4】红黑树插入图解:https://www.cnblogs.com/chenssy/p/3746600.html