安全多方计算-入门学习笔记(三)
四、基于非噪音的安全多方计算介绍
1概念
非噪音方法一般是通过密码学方法将数据编码或加密，得到一些奇怪的数字，而且这些奇怪的数字有一些神奇的性质，比如看上去很随机但其实保留了原始数据的线性关系，或者顺序明明被打乱但人们却能从中很容易找到与原始数据的映射关系(但是对于数据量大的内容，其处理需要消耗的资源非常多)。
2.方法分类
主要包括三种：混淆电路（Garbled Circuit）、同态加密（Homomorphic Encryption）、密钥分享（Secret Sharing）。
这些方法一般是在源头上就把数据加密或编码了，计算操作方看到的都是密文，因此只要特定的假设条件满足，这类方法在计算过程中是不会泄露信息的。
比如计算函数 的时候，实际操作的是 （这里 是 的密文）。
3.优缺点
优点：是不会对计算过程加干扰，因此我们最终得到的是准确值，且有密码学理论加持，安全性有保障，
缺点：则是由于使用了很多密码学方法，整个过程中无论是计算量还是通讯量都非常庞大，对于一些复杂的任务（如训练几十上百层的CNN等），短时间内可能无法完成。而且对于密码学基础薄弱的程序猿来说，要实现前一类基于噪音的方法没啥难度，但要实现后一类方法则还是要费不少功夫的。
五、混淆电路Garbled Circuit
1.混淆电路的工作原理
混淆电路就是通过加密和扰乱电路的值来掩盖数据信息的。
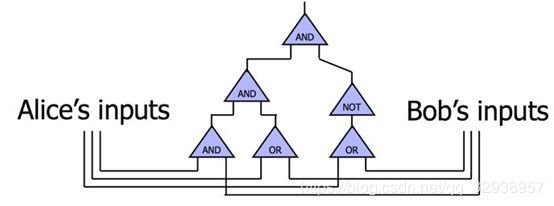
我们知道可将计算问题都可以转换为一个个电路，于是就有了加法电路、比较电路和乘法电路等等。当然，更复杂的计算过程，如深度学习等等，也是可以转换成电路的。一个电路是由一个个门（gate）组成的，比如与门、非门、或门、与非门、异或门(XOR)等等。
如上图所示，电路里面有一些门，每个门包括输入线（input wire）和输出线（output wire）。
2.单个电路的混淆电路设计工作原理
加密和扰乱是以门为单位的。每个门都有一张真值表。比如下图就是与门的真值表和或门的真值表。
(1)加密混淆过程：
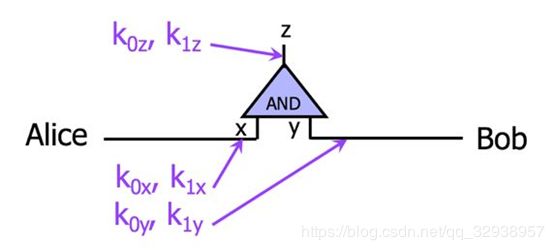
Alice和Bob想计算一个与门。该门两个输入线 x 和 y 和一个输出线 z ，每条线有0和1两个可能的随机值。Alice首先给每条线指定两个随机的key(密钥)，分别对应0和1。
然后，Alice用这些密钥加密真值表(加密过程就是将真值表中每一行对应的( x ，y、 z 的密钥)去加密真值表对应的值)，并将该表打乱(只调换行位置，输入输出的对应值肯定不能变化)后发送给Bob。这一加密+打乱的过程，就是混淆电路（garbled circuit）的核心思想。
(2)解密分析过程：
那Bob收到加密表后，如何计算呢？
首先Alice把自己的输入对应的key(密钥)发给Bob，比如Alice的输入是0，那就发 
(输入是1就发 
)[说明：此时由于真值表是加密且打乱状态,Alice发送的密钥被他人获取(包括Bob)也是属于无用数据，因为加密过程是A操作的]。同时把和Bob有关的key都发给Bob，也就是 
和 
两个密钥都发送给Bob。然后Bob根据自己的输入挑选相关的
或是
，并且根据收到Alice的 
和自己的 
，对上述加密表的每一行尝试解密，最终只有一行能解密成功，并提取出相应的 
。
Bob将Kz发给Alice，[说明：此时对于Bob来说，自身的数据为自己控制输入，他人无法获取，自身数据得到保护，而发送给Alice的Kz结果对于Alice来说并不知道数据源]Alice通过对比是 
还是 
得知计算结果是0还是1，从而解密得到最后结果，由于整个过程大家收发的都是密文或随机数，所以没有有效信息泄露。
(3)流程图如下：
以上就是混淆电路中单个门的计算方法。当然每个电路肯定是由多个门组成的，这时候需要将这些门都串起来。当然，这样的混淆电路方法有点复杂，现在大家已经研究出了很多优化方法，具体方法可以去看论文。
[1] Kolesnikov, Vladimir, and Thomas Schneider. "Improved
garbled circuit: Free XOR gates and applications." International Colloquium on
Automata, Languages, and Programming. Springer, Berlin, Heidelberg, 2008.
[2] Yao, Andrew Chi-Chih. "How to generate and exchange
secrets." Foundations of Computer
Science, 1986., 27th Annual Symposium on. IEEE, 1986.
六、密钥分享(Secret Sharing)
(对混淆电路处理复杂运算à密钥分享)
1.基本原理
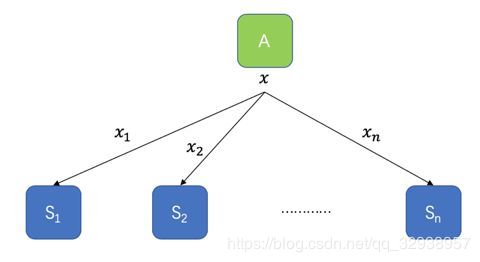
(1)获取数据。将每个数字 x 拆散成多个数 x1,x2,x3,…,xn ，并将这些数分发到多个参与方 S1,S2,…Sn 那里。然后每个参与方拿到的都是原始数据的一部分，一个或少数几个参与方无法还原出原始数据，只有大家把各自的数据凑在一起时才能还原真实数据。
(2)各个服务器计算。各参与方直接用它自己本地的数据进行计算，并且在适当的时候交换一些数据（交换的数据本身看起来也是随机的，不包含关于原始数据的信息），计算结束后的结果仍以secret sharing的方式分散在各参与方那里
(3)得出结果。所有服务器最终将所有计算结果数据合起来，得出最终数据。这样的话，密钥分享便保证了计算过程中各个参与方看到的都是一些随机数，但最后仍然算出了想要的结果。
2.阈值密钥分享
定义一种名为 (t,n) 阈值密钥分享的方案，此类方案允许任意 t个参与方将秘密数据解开，但任何不多于 t-1个参与方的小团体都无法将秘密数据解开。
2.1思想：
假设A想要使用 （t，n） 阈值密钥分享技术将某秘密数字 s 分享给S1,S2,S3,….,Sn，那么他首先生成一个 t-1 次多项式多项式 
，其中 a0 就等于要分享的秘密数字 s ，而 
，则是A生成的随机数。随后A只需将
分别发给(S1,S2,S3,….,Sn)（s1,s2,s3,….,sn值A可事先算出吧）即可， 
中任意 t 个凑在一起构成t个方程组，t个变量(a0,a1a2..at)则可以解出a0的值，而任意 t-1 个凑在一起都无法得到 a0 （即 s ）的确切解。通过这一点便达到了 （t，n） 阈值的要求，同时也满足加法同态。
2.2多发计算，实现乘法计算：
使得(S1,S2,S3,….,Sn能在计算发生前预先得到两个随机数 a 和 b 的秘密分享，以及 a 和 b 的乘积 c 的秘密分享，而且它们都不知道 a 和 b 和 c 的真实值，如下图所示：
现在有A和B分别分享了两个数字 x 和 y ，参与方需要算出 x 和 y 的乘积 z 的密钥分享。
可以借助前面生成的随机乘积元组。我们令 s=x-a 以及 t=y-b ，然后我们可以看到
参与方S1,S2,S3,….,Sn可以联合起来{s+t=x+y-(a+b)；s-t=x-y+b-a}将 s 和 t 的值解开，由于 a 和 b 都是值未知的随机数，因此 s 和 t 的值并不会暴露关于 x 和 y 的信息。上面那个式子中， s*t,s*b,a*t 以及 c 的值可计算出来，因此这几项合起来便能得到 z=x*y 的密钥分享。
七、同态加密（Homomorphic Encryption）
刘巍然-学酥
https://www.zhihu.com/people/liu-wei-ran-8-34
Ph.D/公钥加密/数据隐私保护/Java/
如果未来真的做出了Practical Fully Homomorphic Encryption，那么Gentry一定可以得到图灵奖。哭死！
1.概念
同态加密提供了一种对加密后的数据进行处理的功能。其他人可以对加密后的数据进行处理，但是处理过程不会泄露任何原始内容，同时，拥有密钥的用户对处理过的数据进行解密后，得到的正好是处理后的结果。
数据处理运行流程：
- Alice对数据进行加密。并把加密后的数据发送给Cloud；
- Alice向Cloud提交数据的处理方法，这里用函数f来表示；
- Cloud在函数f下对数据进行处理，并且将处理后的结果发送给Alice；
- Alice对数据进行解密，得到结果。
2.应用
同态加密几乎就是为云计算而量身打造的！我们考虑下面的情景：一个用户想要处理一个数据，但是他的计算机计算能力较弱。这个用户可以使用云计算的概念，让云来帮助他进行处理而得到结果。但是如果直接将数据交给云，无法保证安全性啊！于是，他可以使用同态加密，然后让云来对加密数据进行直接处理，并将处理结果返回给他。这样一来：
• 用户向云服务商付款，得到了处理的结果；
• 云服务商挣到了费用，并在不知道用户数据的前提下正确处理了数据；
3.同态加密的两类：
Fully Homomorphic Encryption (FHE)全同态：这意味着HE方案支持任意给定的f函数，只要这个f函数可以通过算法描述，用计算机实现。显然，FHE方案是一个非常棒的方案，但是计算开销极大，暂时还无法在实际中使用。
Somewhat Homomorphic Encryption (SWHE)：这意味着HE方案只支持一些特定的f函数。SWHE方案稍弱，但也意味着开销会变得较小，容易实现，现在已经可以在实际中使用。
最最经典的RSA加密，其本身对于乘法运算就具有同态性。Elgamal加密方案同样对乘法具有同态性。Paillier在1999年提出的加密方案也具有同态性，而且是可证明安全的加密方案哦！后面还有很多啦，比如Boneh-Goh-Nissim方案[BGN05], Ishai-Paskin方案等等。不过呢，2009年前的HE方案要不只具有加同态性，要不只具有乘同态性
4.面临的问题
效率。一个是加密后的数据的处理速度，一个是这个加密方案的数据存储量
1.精准度会变差。加密后的数据处理与现有原数据在构造上会有差别，处理会出现误差。
2. 密文的操作花费更长的时间
3.算法要求更高
4.更大的存储容量需求