阅读笔记Learning Graph Convolutional Network for Skeleton-based Human Action Recognition by NS(AAAI2020)

---

Abstract

  以图形卷积网络（GCN）为核心的骨架数据的人体动作识别以其强大的非欧几里得结构数据建模能力而备受关注。然而，现有的许多GCN方法都是提供了一个预定义的图，并通过整个网络对其进行修正，导致丢失了隐式的关节关联。此外，主流的谱GCN近似为一阶hop，因此不涉及高阶连接。因此，探索一个更好的GCN体系结构需要付出巨大的努力。为了解决这些问题，作者转向神经架构搜索（NAS），并提出了第一个自动设计的用于基于骨架的动作识别的GCN。具体来说，在充分挖掘节点间的时空相关性之后，作者通过提供多个动态图模块来丰富(enrish)搜索空间。此外，作者还引入了multiple-hop模块，以期突破一阶近似引起的代表能力的限制(就是说one-order hop代表动作能力较小，有一定局限性)。此外，本文还提出了一种有效的取样和记忆进化策略，以寻找此任务的最佳架构。该体系结构证明了高阶近似和具有时间交互的动态图建模机制的有效性，这点以前的论文中很少提到。为了评估搜索模型的性能，我们在两个非常大的数据集上进行了大量的实验，结果表明我们的模型得到了最好(the state-of-the-art)的结果。

Introduction

  人类行为识别是一个有价值但具有挑战性的研究领域，具有广泛的潜在应用，如(say)安全监控、人机交互和自动驾驶等。目前，骨架数据作为一种替代彩色图片(appearance)和深度数据的方法，在动作识别中得到了广泛的应用。一个重要的原因是骨骼数据传递的是身体运动的紧凑信息，因而对视点变化、遮挡和自遮挡等复杂环境具有较强的鲁棒性。以前的工作是将骨架数据重组为一种网格形状结构，如此以至于RNN和CNN能够被使用。尽管在行动认知方面已经有了实质性改进，但它并没有完全受益于深度学习的卓越表现能力，因为骨骼数据位于非欧几里得几何空间中。Currently, Graph Convolutional Networks (GCN) (Kipf and Welling 2016; Defferrard, Bresson, and Vandergheynst 2016) has been introduced to skeleton-based action recognition and achieved many encouraging results (Li et al. 2018; Yan, Xiong, and Lin 2018; Li et al. 2019a; Gao et al. 2019; Shi et al. 2019; Li et al. 2019b)。尽管如此，大多数GCN方法都是基于具有固定拓扑约束的预定义图结构，忽略了隐含的关节关联，2s-GCN将固定的图替换为基于节点相似性自使用图网络。然而，它在整个网络中提供了一种共享机制，而是时空相关性很少被讨论。作者认为不同的层包含不同的语义信息，因此需要一种特定与层的机制来构造动态图。除此之外，主流GCN倾向于一阶切比雪夫多项式近似，以减少计算开销，同时高阶连接没有很好的参与，因此表示能力有限。当前的工作，比如(Gao et al.2019),介绍了高阶近似，使GCN具有更大的感受野。然而，并没有讨论每个分量在近似值中的贡献。显然，为不同的任务设计这样不同的功能模块需要付出大量的努力，并且需要进行大量的尝试和错误测试。
  为了解决这个问题，在论文中，作者着重减少在设计更好的图形卷积体系结构方面的人工工作。作者使用自动神经架构搜索(Neural Architecture Searching, NAS)取代固定的图结构，并在不同语义层次上搜索了不同的图生成机制。NAS的设计目的是在合理的计算预算下，以较少或者不需要人工辅助的方式获得优越的神经网络结构。然而，将NAS应用于GCN并非易事(straightforward)。像骨架这样的图数据没有卷积运算所需要的局部性和顺序信息，而目前的NAS方法侧重于神经网络的设计。除此之外，GCN本身是一个相对比较新的研究领域，现有的业务非常有限，比如GCN甚至还没有一个通用的池化操作。因此，作者建议在一个由多个图函数模块构成的GCN空间中进行搜索。此外，还提供了一种高样本效率的深度神经进化策略(deep neuro-evolution strategy (ES) ),通过估计结构分布来搜索最优的GCN结构。它可以在连续搜索空间和离散搜索空间中进行，因此，我们可以在每次迭代时激活一个功能模块，以一种节省内存的方式进行搜索。利用作者的用于GCN的NAS，作者自动构建了一个用于从骨架数据中进行动作识别的图卷积网络。为了评估该方法，作者对两个大型的数据集NTU RGB+D以及Kinetics Skeleton。结果表明，作者的模型对subject和view的变化具有鲁棒性，并达到了最优的性能。论文主要贡献：

• 突破了GCN固定图的局限性，首次用NAS确定了基于骨架的动作识别的图形卷积结构。
• 论文从以下两个方面丰富了GCN的搜索空间。首先，在各种时空图模块的基础上，给出了多个动态图子结构。其次，利用Chebyshev多项式逼近建立高阶连接，扩大了GCN卷积的接收场。
• 为了提高搜索效率，作者设计了一种新的基于进化的NAS搜索策略，该策略既具有采样效率又具有记忆效率。

Relate work

Skeleton-based Action Recognition在人体动作识别中，骨骼数据作为RGB和深度数据的替代数据源，由于其对人体尺度、视点和背景变化的鲁棒性，越来越受到人们的关注。不同于网格数据，由人体骨架构造的图位于非欧几里得空间中。为了利用深度学习的强大表示能力，传统的方法倾向于将骨架数据重新排列成网格形状结构，并直接将其输入到经典的RNN中（Shahroudy等人。2016年；Song等人。2017年；Zhang等人。或CNN结构（Kim and Reiter 2017；Liu，Liu，and Chen 2017）。然而，如（Monti等人。2017），不能在顶点域中表示有意义的算子。因此，目前的研究倾向于在非欧几里得空间中建立GCN算子。林达华组是最早使用GCN进行基于骨骼的动作识别。Gao等人。提出了一种基于稀疏图回归的GCN（Gao等人。2019年）利用各关节的依赖性。Shi等人。给出了一种双流GCN结构，其中关节和二阶信息（骨骼）都被使用。采用分数级(score-level)融合策略,它得到了当前最好的结果（Shi等人。2019年）本文的方法也是基于GCN的，作者将充分探讨图形拓扑对这项任务的影响。
Neural Architecture Search作为自动机器学习（AutoML）的一个重要组成部分，神经架构搜索（NAS）旨在以较低的计算资源成本自动构建神经网络。文献中已经存在许多针对NAS的方法，包括基于强化学习的黑箱优化、进化搜索，以及基于梯度的方法。此外，在搜索空间设计（Liu、Simonyan和Y ang 2018）和结构性能评估（Saxena和V erbeek 2016）等方面也取得了可喜的进展。在图像分类任务等领域，自动设计的体系结构已经比著名的手工设计的体系结构有了更优越的性能（Zoph等人。2018），以及语义图像分割（Liu等人。2019年）。在rgb数据集中，NAS在动作识别方面也有一些尝试（Peng、Hong和zhao2019）。然而，基于little NAS的方法为非欧数据提供了一种解决方案。事实上，目前Gao等人转化ENAS为引文网络和归纳学习任务绘制神经网络图。但是，与本文的任务相比，它完全不同，因为它的目标是找到只有两层或三层网络的转换、传播和聚合功能。
GCN and Attention mechanism图形神经网络广泛应用于社会网络、生物数据等不规则数据。一般来说，定义GCN有两种方法。

• 谱域法，基于特征分解对图形傅里叶变换域中的表示进行建模，同时很费时。
• 节点域方法，直接在图节点及其邻域上实现GCN。但是很难对全局结构进行建模。
  为了进一步提高GCN性能，在GCN中引入注意力机制。注意力机制的一个好处是，从所有输入中选择相对重要的信息。受此启发，Velickovic等人利用注意机制对图形节点进行分类，并取得了state-of-the-art的性能（Veliˇckovi’c等人。2018年）。（Sankar等人。2019）在空间和时间维度上运用自我注意，在链路预测任务上获得优异的结果。尽管如此，本文的工作是不同的，因为作者根据不同的语义信息计算节点之间的交互来构建动态图，而其他工作是计算帧或不同特征表示的重要性权重。

Methodology

  在本节中，我们将详细介绍(detail)基于搜索的GCN，用于从骨骼数据中识别动作。为了使论文具有自包含性，作者首先简要回顾了如何用GCN建立空间图的模型。
  无向图网络$G=\{V,ϵ,A\}$，然后，为了对$G$的表示进行建模，对该图进行图傅里叶变换，以便变换后的信号（如在欧几里得空间中）可以随后执行基本操作（如滤波）。因此，图的拉普拉斯L，其规范化定义为$L=I_n-D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}$，$D_{ii}={\sum }_j{A}_{ij}$,用于傅里叶变换。然后，由算子$g_{\theta }$滤波的图，由$\theta$参数化，可以表示为$$Y=g_{\theta }(L)X=U{g}_{\theta }(\Lambda )U^{T}X$$其中Y是节点的特征提取，U是傅里叶变换基，它是L的一组正交特征向量，因此$L=U\Lambda U^T$,$\Lambda$作为其对应的特征值。然而，与特征向量矩阵相乘复杂度非常高的。这种非参数滤波器的计算量为$\mathrm{O}(n^2)$。滤波器$g_{\theta }$可以很好的用R阶切比雪夫多项式逼近。$$Y=\sum _{r=0}^R{\theta }_r^{\prime }{T}_r(\hat{L})X$$
其中${\theta }_r^{\prime }$表示切比雪夫系数，切比雪夫多项式$T_r(\hat{L})$递归定义为：$$T_r(\hat{L})=2\hat{L}{T}_{r-1}(\hat{L})-T_{r-2}(\hat{L})$$当$T_0=1$，$T_1=\hat{L}$。这里$\hat{L}=2L/{\lambda }_{max}-I_n$是归一化操作[-1,1]。对于R阶切比雪夫不等式，$R=1,{\lambda }_{max}=2$,使网络适应此变化。这样，就形成了谱图卷积的一阶近似，因此，$$Y={\theta }_0^{\prime }X+{\theta }_1^{\prime }(L-I_n)X={\theta }_0^{\prime }X-{\theta }_1^{\prime }(D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}})X$$同样的，${\theta }_r^{\prime }$也可以用一个统一的参数$\theta$来近似，也就是说$\theta ={\theta }_0=-{\theta }_1$，并让训练过程适应近似误差，then$$Y=\theta (I_n+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}})X$$。计算的复杂度为$\mathrm{O}(|ϵ|)$。一个可以叠加多个GCN层来获得高层次的图特征。为了简单起见，作者设置了$L=I_n+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}$并且通常情况下，$X\in {\mathcal{R}}^{n\times C}$具有多通道。因此$$Y=LX\theta$$
Searched Graph Convolutional Network
Here 我们把骨骼数据中的人类行为识别问题看作是一个图序列$\mathbb{G}=G_1，G_2，\dots ，G_T$的图分类任务。每个图表示一个在某时间步上骨骼信息，其节点和边分别代表骨骼关节点和骨骼。Then，将此类任务构造为图数据上的有监督学习问题，其目标是利用GCN学习$\mathbb{G}$的鲁棒表示，从而更好地预测动作类。为此，我们提出用神经结构搜索来构造这个GCN，它可以自动地为不同语义层次的层组装图形生成模块。首先，我们将详细说明用不同的图模块构建的GCN搜索空间。然后，我们提出了一个样本和记忆有效的搜索策略。
GCN search space在NAS中，一个神经搜索空间决定了一个搜索策略可以采取什么样的神经操作来建立一个神经网络。本文在多个GCN模块构成的空间中搜索动态图在不同表示层次上的最优模块组合。AAAI2018文中给出了一个以骨架数据和固定图为输入的ST-GCN块，用于提取节点的时空表示。我们的GCN块也是一个时空块，而不是提供一个预定义的图，而是根据不同功能模块捕获的节点相关性生成动态图。动态图的构造主要有两种相关关系。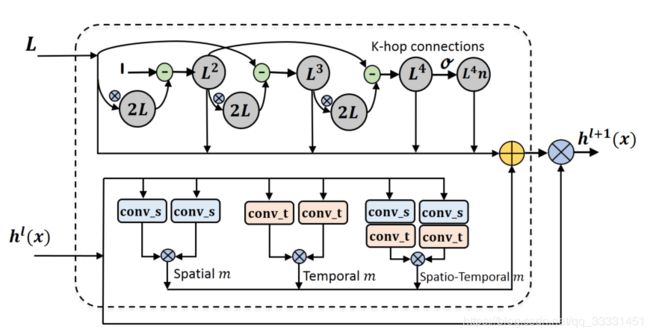
图1.搜索空间的图示。Here,$\otimes$表示矩阵乘法，$\oplus$表示元素求和。有八个功能模块用于生成图。第一部分是基于切比雪夫多项式实现的。作者还将其独立的组件添加到图中，让网络选择最终的组件。底部包含3个动态图模块。根据式8将所有的图相加，每个模块的贡献作为架构参数。注意，在动态图的求和操作之前就有一个softmax函数。
Structure representation Correlation基于空间节点连接计算结构相关性。以确定两个节点之间的连接有多强，比如2s-GCN，在图节点上应用归一化高斯函数，相似度作为相似性。That is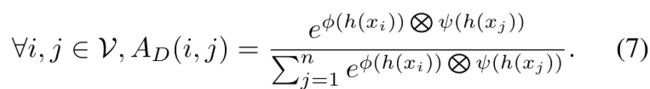

这个模块在图1中被命名为“Spatial m”。在这里，我们计算节点$i$和节点$j$之间的相关得分$A_D(i,j)$，基于它们的对应表示$h(x_i)$和$h(x_j)$。$\otimes$表示矩阵乘法。φ(·)和Ψ(·)是两个投影函数，在图1中称为conv_s，可通过信道卷积滤波器实现。这样，就可以捕获节点之间的相似性来构建动态图。
Temporal representation Correlation结构关联无疑包含了最直观的图形拓扑线索。然而，忽略时间相关性会丢失隐含的联合相关性。我们以南洋理工大学RGB+D数据集为例。没有时间信息，很难告诉一个人是摸他的头还是只是挥手。从物理结构的角度看，在头部和手部的接触过程中，头部和手部之间的连接很少。但是这次action中，它们之间应该有关联。如果包括时间信息就会很容易的找到关联。因此用等式7来计算节点相关性之前，作者引入两个时间卷积来提取时间信息。In this way，在计算节点连接时，就涉及到相邻帧之间的节点交互。注意，这里的时间表示相关性不同于时间注意机制，时间注意机制是给相对重要的帧赋予更高的权重。相比之下，作者捕获时间信息以更好地生成空间图。在这方面，还引入高斯函数，如等式（7）中所述，以计算节点相关性。函数$\varphi (\cdot )$和$\psi (\cdot )$通过时间卷积实现，在图1中称为conv_t，此模块称为"Temporal m"。值得一提的是，对于结构相关性，即使是T帧的表示都涉及到图的计算，交互作用也仅限于同一时间步长下同一维度的特征。而我们的时间模块可能涉及到同一帧之外的交互。
  利用这两个模块‘Spatial m’和‘Temporal m’，可以直接构建动态图的时空功能模块。因此，我们构建了图1中的“Spatio-Temporal m”。因此，如图1所示，动态图有三种模块。
  此外，我们还想探讨切比雪夫多项式中各分量的贡献，从而从高阶跳连接中获益。我们知道，(Kipf和Welling 2016)中的工作给出了一阶Chebyshev多项式谱滤波器的良好近似。Instead，如图1所示，在我们的搜索空间中，我们在不同的层上构建不同阶数的Chebyshev多项式函数，并让网络确定每层优先选择的阶数和多项式分量。函数模块可以由切比雪夫多项式构造，最大的order是$R=4$。因为所有的动态图都是规范化(normalized)的，所以在这里我们还为order-4近似添加了一个规范化的图。因此，如图1所示，在这个搜索空间中总共有八个功能模块。
  有了这八个模块，我们可以寻找最佳的架构。以前的NAS方法会搜索一个块来减少计算负担。然而，我们认为不同的特征层包含不同层次的语义内容，因此最好使用特定于层的机制来构建图。所以我们搜索整个GCN网络而不是单个块。为了提高效率，将提供一种高计算和内存效率的搜索策略。
  让我们先正式定义搜索空间。这里我们把$X$重新定义为一系列图。给定一个固定的图$L$和第k层的特征$h^k(X)$，我们在k+1层提取输出表示$h^{k+1}(X)$,并选择相应的功能模块。受one-shot NAS和DART的启发，所有的功能模块都是并行的，其输出的加权和为输出$h^{k+1}(X)$,that is$$h^{k+1}(X)=\sum _{i=1}^M\frac{{\alpha }_{k+1,i}}{{\sum }_j^M{\alpha }_{k+1,j}}{\mathcal{M}}_i(h^k(X),L)h^k(X){\Theta }_k(8)$$Here, ${\Theta }_k$是k层网络权重。${\mathcal{M}}_i$是第i个功能模块，${\alpha }_{k+1,i}$作为架构参数，是它在k+1层的对应参数。之后在K层网络中搜索一组参数$\alpha \in R^{K\times M}$，使$\alpha$在验证数据中的损失最小。That is，$$\alpha \ast =\underset{\alpha }{\mathrm{argmin}}{L}_{valid}(\Theta (\alpha ),\alpha )(9)$$Here, Θ是所有子网共享的网络参数，它将在训练数据集上学习。以前的工作是在一个小的代理数据集上搜索以避免昂贵的计算负担。相反，这里我们直接搜索目标数据集以避免引入额外的域自适应问题
GCN search strategy灵感来自（Pou.and S.2019），我们建议使用基于高采样效率ES的方法进行搜索，表示为CEIM。该方法通过估计体系结构的分布来探索最优体系结构。因此它不受可微搜索空间的限制。每个搜索步骤只需激活一个功能模块，就可以提高存储效率。
  具体地说，这种搜索策略结合了交叉熵方法和重要混合（CEIM）来提高采样效率。在CEIM中，结构参数α被看作一个总体，结构的分布用高斯分布来模拟。然后CEIM对一组体系结构进行采样，并根据它们的性能选择重要的样本来更新体系结构分布。因此，可以最终从架构分布中抽取最佳架构。在我们的CEIM算法中，总共有三个步骤：抽样总体、选择总体和更新体系结构分布。首先用高斯分布$\pi \sim N(\mu ,\delta )$对体系结构分布进行建模，样本N体系结构$S_{new}$是CEIM的总体，即$S_{new}=\{{\alpha }_n^i{\}}_{i=1}^N$。secondly,结合$S_{new}$与历史选择人员$S_{old}$，我们对所有这些群体采用重要性混合方法来选择结构样本。Finally,新选择的样本用于更新体系结构分布$\pi$。
  Here，我们详细介绍了最后的两个步骤。假设前一次迭代的样本是$S_{old}=\{{\alpha }_o^i{\}}_{i=1}^N$。在选择的步骤中，针对$S_{new}$和$S_{old}$每个群体，比较了当前(${\pi }_{new}$)和旧有(${\pi }_{old}$)概率密度函数（pdf）中的概率密度（pd）。一般来说，对于旧有的population ${\alpha }_o^i$我们在新分布中保留它，当它的概率密度大于旧分布时。That is$$\min (1,\frac{p({\alpha }_o^i;{\pi }_{new})}{p({\alpha }_o^i;{\pi }_{old})})>r1$$这里的$r1$是[0,1]中随机获取的阈值，$p(\cdot ;\pi )$是一个具有特定分布的$\pi$的概率密度函数。同理，对于新样本${\alpha }_o^i$来自于当前分布，如果新的概率密度函数中的概率密度大于旧pdf中的pd，我们会保留。因此，当$$\max (0,1-\frac{p({\alpha }_o^i;{\pi }_{new})}{p({\alpha }_o^i;{\pi }_{old})})>r2$$我们保留它，$r2$是另一个阈值，范围[0,1]。
  对于更新step，使用上一step中选择的样本更新平均值$\mu$和方差$\sum$。在此之前，网络的$\Theta$根据当前结构$\alpha =\mu$训练数据进行更新。然后，固定$\Theta$，并将每个选定的样本设置为当前结构。根据验证数据对其相应的适应度进行了评价。根据它们的性能，对所有选定的样本进行排序。根据性能顺序，为第i个样本分配重要权重${\lambda }_i$.That is$${\lambda }_i=\frac{\log (1+N)/i}{{\sum }_{i=1}^N\log (1+N)/i}$$
In this way,性能较好的样本将被赋予更大的权重，从而对分布的更新贡献更大。最后，加权样本被应用到更新结构分布中。That is$${\mu }_{new}=\sum _{i=1}^N{\lambda }_i{\alpha }^i,$$$$\sum _{new}=\sum _{i=1}^N{\lambda }_i({\alpha }^i-\mu {)}^2+ϵ\mathcal{I}$$Here,$ϵ\mathcal{I}$是噪声项，为了更好的探寻神经结构。因为在实际中，$\sum$太大，无法计算和更新，所以这里我们将其限制为diag。注意，上式中，不同于原始的交叉熵方法，该方法用新的平均值${\mu }_{new}$更新$\sum$,我们使用上次迭代的平均值来更新$\sum$,因为协方差矩阵自适应进化策略(CMA-ES)表明它更有效。更多的CEIM细节可以参考上述算法图。
  每个搜索步骤只需要激活一个功能模块就可以提高存储效率。这意味着对于输出$h^{k+1}(X)$，它可以是激活模块的单个输出。$$h^{k+1}(X)=\{\begin{array}{l}{\mathcal{M}}_1(h^k(X),L)h^k(X){\Theta }_{k+1},p=\frac{{\alpha }_{k+1,1}}{{\sum }_j^M{\alpha }_{k+1,j}}\\ ...\\ {\mathcal{M}}_M(h^k(X),L)h^k(X){\Theta }_{k+1},p=\frac{{\alpha }_{k+1,M}}{{\sum }_j^M{\alpha }_{k+1,j}}\end{array}$$这里，每个模块被多项式分布激活，概率$p\sim {\alpha }_{k+1}$，${\Theta }_{k+1}$是第（k+1）层的激活权重。在下一节中，我们将评估所建议的方法。
结论见作者知乎