阅读笔记Actional-Structural Graph Convolutional Networks for Skeleton-based Action Recognition(CVPR2019)

  cv小白拜读Actional-Structural Graph Convolutional Networks for Skeleton-based Action Recognition(CVPR2019)，论文是在AAAI2018 ST-GCN的基础上进一步发展而来。论文结构调理清晰，源代码也已经给出，便于深入理解。
Paper：Actional-Structural Graph Convolutional Networks for Skeleton-based Action Recognition
Code：Github:https://github.com/limaosen0/AS-GCN

---

Abstract

  基于骨骼数据的动作识别是近年来计算机视觉领域的研究热点。以往的研究大多数基于固定的骨架图，仅仅捕获关节之间的局部物理关系，这样可能会丢失隐性的关节点相关性。为了捕捉更丰富的依赖关系，论文介绍了一种编解码结构，称为A-link推理模块。直接从动作中捕捉特定的潜在依赖关系，即动作链接。作者还拓展了现有的骨架图来表示更高阶的依赖关系，即结构链接。将这两种类型的链接组合成一个广义骨骼图，作者进一步提出了动作结构卷积网络(Actional-Structural, AS-GCN),网络将动作结构图卷积和时间卷积作为一个基本的构建块(a basic building block), 学习动作识别的时空特征。在识别的同时增加一个未来姿势预测头(prediction head),通过自我监督帮助捕捉更详细的动作模式。作者在两个数据集(NTU-RGB+D和Kinetics)上对AS-GCN进行了动作识别验证。提出的AS-GCN相比现有技术方法，具有更大的改进空间。除此之外(side product)，As-GCN在未来的位姿预测中也显示出了良好的效果。

1. Introduction

  人类行为识别广泛应用于视频监控、人机交互、虚拟现实等领域，近年来受到计算机视觉领域的广泛关注。骨骼数据，动态三维关节位置坐标，在动作识别中已经被证明是有效的，对传感器噪声具有一定的鲁棒性，并且在计算和存储上是有效的。骨骼数据通常是通过深度传感器定位关节的2D或3D空间坐标，或者是使用基于视频的姿态估计算法获得。
  最早的动作识别尝试通常将每个帧中的所有身体关节位置编码为用于模式学习的特征向量。这些模型很少探索人体关节之间的内在依赖性，从而失去了大量的动作信息。为了获取关节相关性，最近的方法构造了一个懂点为关节，边为骨骼的骨架图，并应用图卷积网络(GCN)提取相关特征。时空图卷积网络(ST-GCN)更好的发展了GCN特性，同时学习了空间和时间特征。但是，ST-GCN虽然提取了直接通过骨骼连接的关节特征，但是在结构上较远的关节(可能包括关键动作的模式)却被忽略了。例如，当走路的时候，手和脚是紧密相关的。当ST-GCN试图用分层GCN聚合更广泛的特征时，在复杂长距离网络中(long diffusion)，节点特征可能会减弱。
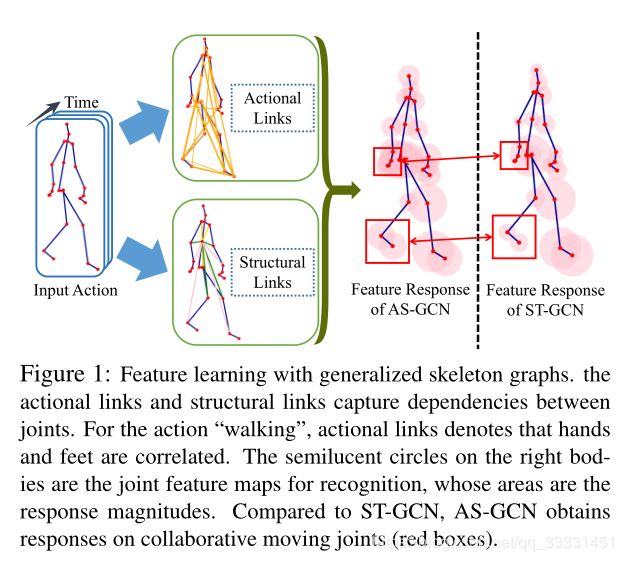
  论文试图通过构造广义骨骼图来获取关节间更丰富的依赖关系。特别是，通过数据驱动判断动作链接(A-links)来捕获所有关节之间的依赖关系。文章提出了一种具有编解码结构的A-link推理模块(AIM)。作者拓展了骨架图，将高阶关系表示为结构链接(S-links)。基于具有A-links和S-links的广义图，提出了一种动作结构图卷积方法来获取空间特征。论文进一步提出了动作结构图卷积网络(AS-GCN),网络将动作结构图卷积和时间卷积叠加在一起。作为一种backbone网，AS-GCN可以适应各种任务(tasks)。本文以动作识别为主要任务，以未来姿态为次要任务。预测头通过保留细节特征来促进自我监督和提高识别率。图1显示了AS-GCN模型的特点，在该模型中，模型学习动作扩展用于动作识别的结构链接。通过(实验)特征显示，我们可以获取比ST-GCN更多的全局链接信息，ST-GCN只使用骨架图来建模局部关系。
  为了验证所提出的AS-GCN的有效性，我们在两个不同的大规模数据集上进行了广泛的实验：NTU-RGB+D和kinetics。实验表明，AS-GCN在动作识别方面优于目前最先进的方法，另外，AS-GCN准确预测未来帧，显示捕获了足够的详细信息。论文的主要贡献概括如下：
1、论文提出了A-link推理模块（AIM），用来推断动作链接，动作链接负责捕捉动作特定潜在依赖性。动作链接与结构链接组合的广义骨骼图，见图1；
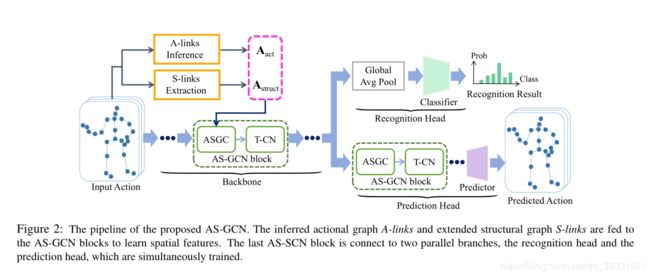
2、论文提出了动作结构图卷积网络（AS-GCN）来提取基于多个图的有用时空信息，如图2所示；
3、论文引入了一个额外的未来姿势预测头，预测未来的姿势，通过捕捉更详细的动作模式来提高识别性能；
4、AS-GCN在两个大规模数据集上的性能优于几种最先进的方法；作为副产品，ASGCN还能够精确预测未来的姿态。

2. Related Works

  骨骼数据在动作识别中有着广泛的应用。大多数算法都是基于两种方法开发的：基于手工制作的和基于深度学习的。第一种方法设计了基于自然物理知识捕捉动作模式的算法，例如局部占用特征、时间联合协方差和李群曲线。另一方面，基于深度学习的方法自动从数据中学习动作特征。一些基于递归神经网络（RNN）的模型捕获了连续帧之间的时间依赖关系，如bi-RNNs、deep LSTMs和基于注意力的模型。卷积神经网络（CNN）也取得了显著的效果，如残差时间CNN、信息增强模型和动作表示CNN。最近，随着灵活地利用肢体关节关系，图方法引起了广泛关注。本文采用基于图的方法进行动作识别。与以往的方法不同，论文从数据中自适应地学习图，从而捕捉到关于动作有用的non-local信息。

3. Background

  在本节中，将介绍论文其余部分所需的基础知识和公式。

3.1. Notations(论文相关符号)

  把骨骼图看做是$G(V,E)$, V是n个关节点的集合，E是m个骨骼的集合(邻接矩阵adj)。令$A\in \{0,1{\}}^{n\times n}$为骨架图的邻接矩阵，如果$i$-th和$j$-th关节是连通的，则$A_{i,j}=1$, 否则为0。$A$完全描述了骨架结构。令$D\in {\mathcal{R}}^{n\times n}$是骨骼图的对角度矩阵，$D_{i,j}={\sum }_j{A}_{i,j}$。为了获取更精细的位置信息，论文将一个根节点相邻的节点分为三组(和ST-GCN一样)，包括1)根节点本身，2)向心群，比根节点更接近身体重心，3)离心群，A相应的分为$A^{(root)}$(根节点)、$A^{(centripetal)}$(向心节点)、$A^{(centrifugal)}$(离心节点)。作者用$\mathcal{P}=\{root,centripetal,centrifugal\}$表示分配群集合。注意${\sum }_{p\in \mathcal{P}}{A}^{(p)}=A$。令$\mathcal{X}\in {\mathcal{R}}^{n\times 3\times T}$为 $T$ 帧时刻的3D关节位置。设$X_t={\mathcal{X}}_{:,:,t}\in {\mathcal{R}}^{n\times 3}$为第t帧的3D关节位置，该关节将时间维度放到最后。设$x_i^t={\mathcal{X}}_{i,:,t}\in {\mathcal{R}}^d$为第i关节在第t帧处的位置。

3.2. Spatio-Temporal GCN(时空图卷积神经网络)

  时空GCN(ST-GCN)由一系列ST-GCN块组成。每个块包含一个空间图卷积和一个时间卷积，后者交替地提取空间和时间特征。最后一个ST-GCN块连接到完全连接的分类器以生成最终预测。空间图卷积运算是STGCN的关键组成部分，它为每个关节引入相邻特征的加权平均。设$X_{in}\in {\mathcal{R}}^{n\times d_{in}}$为一帧中所有关节的输入特征，其中$d_{in}$为输入特征维数，$X_{out}\in {\mathcal{R}}^{n\times d_{out}}$为空间图卷积得到的输出特征，其中$d_{out}$为输出特征维数。空间图卷积是$$X_{out}=\sum _{p\in \mathcal{P}}{M}_{st}^{(p)}◦\widetilde{A^{(p)}}{X}_{in}{W}_{st}^{(p)}$$其中$\widetilde{A^{(p)}}={D^{(p)}}^{-\frac{1}{2}}{A}^{(p)}{D^{(p)}}^{-\frac{1}{2}}\in {\mathcal{R}}^{n\times n}$是标准化邻接矩阵， ◦表示为哈达玛积，$M_{st}^{(p)}\in {\mathcal{R}}^{n\times n}$和$W_{st}^{(p)}\in {\mathcal{R}}^{n\times d_{out}}$ 是每个分区的可训练权重，分别用于捕获边缘权重和特征重要性。

4.Actional-Structural GCN(动作结构GCN)

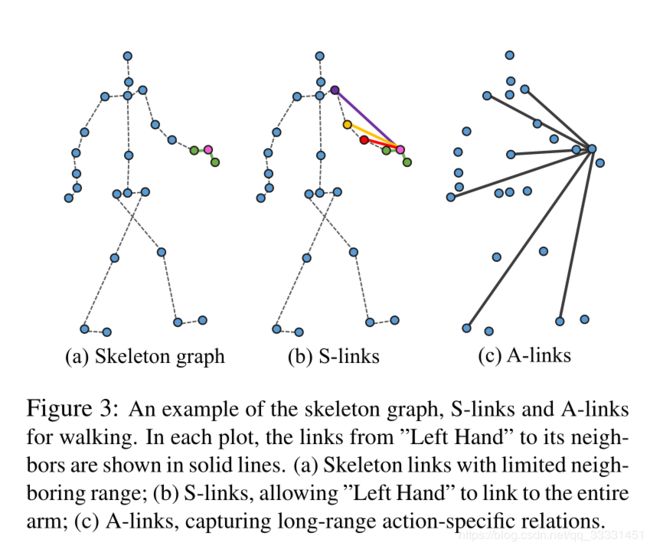
  广义图，即传统结构图，定义为${\mathcal{G}}_g(V,E_g)$,其中V是原始关节点的集合，$E_g$是广义连接的集合。$E_g$有两种类型的链接：结构链接(S-links)，显式获取身体结构；动作链接(A-links),直接从骨架数据推断。参见图3中两种类型。

4.1. Actional Links (A-links)(动作链接)

  许多人类行为需要相隔很远的关节才能协同实现，从而导致关节之间存在非自然连接的依赖性。为了捕获各种动作的相应依赖关系，作者引入动作链接(A-links), 这些链接由动作激活，可能存在任意对关节之间。为了从动作中自动推断出A-links，我们开发了一个可训练的A-link推理模块(AIM)，它由编码器和解码器组成。编码器通过迭代地在关节点和链接之间传播的信息来生成A-links，以学习链接特征；解码器根据推断的A-links来预测未来的关节位置；参看图4。作者使用AIM对A-links进行预分配参数(warm-up)，在训练过程中进一步调整。
Encoder.编码器的功能是在给定3D关节位置的情况下估计A-links的状态，即$$\mathcal{A}=encode(\mathcal{X})\in [0,1{]}^{n\times n\times C}$$其中$C$是A-links的类型数。元素${\mathcal{A}}_{i,j,c}$表示第c中类型的A-links,第$i,j$关节点连接的概率。设计映射编码的基本思想是首先从三维关节位置精确地提取出连接的特征，然后将连接特征转化为连接概率。为了精确的连接特征，作者交替地在关节和链接之间传递信息。在所有T帧上，令$x_i=vec({\mathcal{X}}_{i,:,:})\in {\mathcal{R}}^{dT}$为第i个关节特征的向量。初始化关节特征为$p_i^{(0)}=x_i$。为了获取更高阶的 link features,作者进行了k次迭代，在关节和连接之间更新权值。
link features:$Q_{i,j}^{(k+1)}=f_{\epsilon }^{(k)}(f_v^{(k)}(p_i^{(k)})\oplus (f_v^{(k)}(p_j^{(k)}))$,
joint features:$P_i^{(k+1)}=\mathcal{F}(Q_{i,:}^{(k+1)})\oplus p_i^{(k)}$,
其中，$f_v(\cdot )$和$f_e(\cdot )$都是多层感知器，$\oplus$是向量拼接，$F(\cdot )$是aggregate link features 得到joint features 的操作，例如平均和最大化。在迭代k次后，编码器将链接概率输出为：$${\mathcal{A}}_{i,j,:}=softmax(\frac{Q_{i,j}^{(K)}+r}{\tau }\in {\mathcal{R}}^C)$$其中$r$是一个随机向量，其中元素采样是采样的i.i.d.，服从Gumbel(0,1)分布¹，$\tau$控制${\mathcal{A}}_{i,j,:}$的离散化。这里我们设置$\tau$=0.5。我们通过Gumbel-softmax得到了连接概率${\mathcal{A}}_{i,j,:}$的近似分类形式。

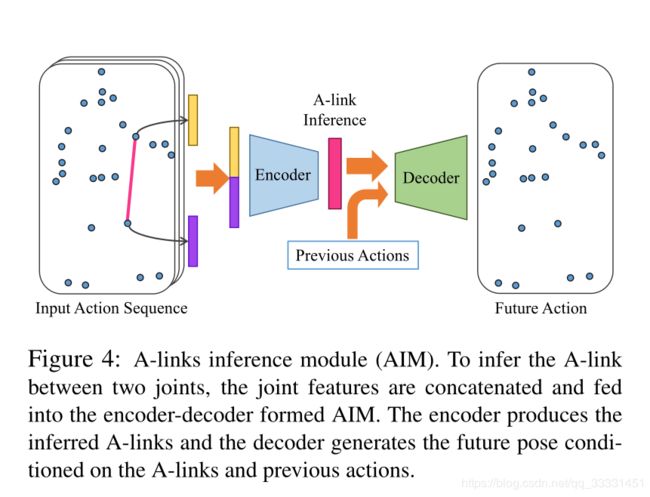
Decoder.解码器的功能，用于预测未来的3D关节位置，利用前T 帧的结点features以及A(link probabilities)去预测t+1帧的节点位置，即$$X_{t+1}=decode(X_t,...,X_1,\mathcal{A})\in {\mathcal{R}}^{n\times 3},$$其中$X_t$是第t帧的3D关节点坐标位置。基本的思想是首先基于A-links提取关节特征，然后将关节特征转化为未来的关节位置坐标。令$x_i^t\in {\mathcal{R}}^d$为第t帧第i个骨骼点的特征。映射解码工作为：
$(a)Q_{i,j}^t={\sum }_{c=1}^C{\mathcal{A}}_{i,j,c}{f}_e^{(c)}(f_v^{(c)}(x_i^t)\oplus f_v^{(c)}(x_j^t))$
$(b)p_i^t=\mathcal{F}(Q_{i,:}^t)\oplus x_i^t$
$(c)S_i^{t+1}=GRU(S_i^t,p_i^t)$
$(d){\tilde{\mu }}^{t+1}=f_{out}(S_i^{t+1})\in {\mathcal{R}}^3,$
其中$f_v^{(c)}(\cdot ),f_e^{(c)}(\cdot )$和$f_{out}(\cdot )$是MLPs。
步骤(a) 通过加权平均求得在t帧时，关节点i,j之间的连接程度。其中link概率${\mathcal{A}}_{i,j,:}$;
步骤(b) aggregates $i$节点与其他节点的$Q_{i,j}^t$,并和$x_i^t$进行拼接，得到$i$节点的joint features $P_i^t$；
步骤(c )使用门控循环单元(GRU)更新关节特征,其中，$S_i^t$表示在$t$层的隐藏状态；
步骤(d)预测了未来关节点位置坐标的平均值。我们最终从高斯分布(即${\hat{x}}_i^{t+1}\mathcal{N}({\hat{\mu }}_i^{t+1},{\sigma }^{2}I)$中采样未来的关节点位置${\hat{x}}_i^{t+1}\in {\mathcal{R}}^3$,其中${\sigma }^2$表示方差，$I$是单位矩阵(identity matrix)。
  我们准备了几个warm-up A-links的epoches。从数学角度分析，AIM的cost function是：
$${\mathcal{L}}_{AIM}(\mathcal{A})=-\sum _{i=1}^n\sum _{t=2}^T\frac{||x_i^t-{\hat{\mu }}_i^t|{|}^2}{2{\sigma }^2}+\sum _{c=1}^{C}log\frac{{\mathcal{A}}_{:,:,c}}{{\mathcal{A}}_{:,:,c}^{(0)}}$$
其中${\mathcal{A}}_{:,:,c}^{(0)}$是$\mathcal{A}$的先验值。在实验中，我们发现当$\mathcal{A}$趋近稀疏时，模型的能力提升越大。直观来看，大多数的连接会捕捉无用的依赖关系，从而导致行为模式学习的冗杂；然而，在公式3，即softmax中，我们保证${\sum }_{c=1}^C{\mathcal{A}}_{i,j,c}=1.$由于概率1被分配给C link，当C很小时，即C link types数量很少的时候，很难提高稀疏性。为了控制稀疏度，作者引入了一个虚链接(ghost link)，表明两个节点没有通过任何一个A-link连接,这种边类型没有实际意义，仅仅用于占用 large probability，虚链路仍然确保概率总和为1；就是说，对于$\forall i,j,{\mathcal{A}}_{i,j,0}+{\sum }_{c=1}^C{\mathcal{A}}_{i,j,c}=1，$其中${\mathcal{A}}_{i,j,0}$是$i,j$节点没有联系的概率。这里我们设置了先验概率${\mathcal{A}}_{:,:,0}^{(0)}=P_0$以及$A_{:,:,c}^{(0)}=P_0/C$,其中$c=1,2,...,C$。在悬链AIM过程中，我们只更新A-links(${\mathcal{A}}_{i,j,c}$)的概率，其中$c=1,...,C$。
  我们对多个样本累积求取${\mathcal{L}}_{AIM}$并将其最小化以获得warm-up $\mathcal{A}$。令${\mathcal{A}}_{act}^{(c)}=A_{:,:,c}\in [0,1{]}^{n\times n}$为第c类连接概率，表示第c类动作图的拓扑结构。我们定义了动作图卷积(AGC)，它使用A-links来捕捉关节点之间的动作依赖关系。在AGC中，我们使用${\hat{A}}_{act}^{(c)}$作为图卷积核，其中${\hat{A}}_{act}^{(c)}={D_{act}^{(c)}}^{-1}{A}_{act}^{(c)}$。给定输入$X_{in}$,AGC为$$X_{a}ct=AGC(X_{in})=\sum _{c=1}^C{\hat{A}}_{act}^{(c)}{X}_{in}{W}_{act}^{(c)}\in {\mathcal{R}}^{n\times d_{out}}，$$
其中$W_{act}^{(c)}$是可训练权重以捕捉特征的重要性。需要注意的是，在预训练过程中，我们使用AIM对A-links进行warm-up；在动作识别和姿态预测的训练中，通过前向传递AIM的编码器，进一步优化A-links。

4.2. Structural Links (S-links)(结构链接)

  在公式1中，在骨骼图中，$\widetilde{A^{(p)}}{X}_{in}$汇聚了1-hop邻域的信息；也就是说ST-GCN在每层中只是局部传递信息。为了获得长距离links，我们使用A的高阶多项式，表示S链路。在这里我们使用${\hat{A}}^L$作为图卷积核，其中$\hat{A}=D^{-1}A$是图的转移矩阵，$L$是多项式的阶数。$\hat{A}$引入度normalization以避免梯度爆炸，并有一定的 probabilistic intuition。利用L阶多项式定义了结构图卷积(SGC)，该卷积可以直接到达L-hop邻域以增加感受野。SGC的表述如下：$$X_{struc}=SGC(X_{in})=\sum _{l=1}^L\sum _{p\in \mathcal{P}}{M}_{struc}^{(p,l)}◦{\hat{A}}^{(p)l}{X}_{in}{W}_{struc}^{(p,l)}$$
$$\in {\mathcal{R}}^{n\times d_{out}}，$$其中$l$是多项式阶数，${\hat{A}}^{(p)}$是第p部分的图转移矩阵，$M_{struc}^{(p,l)}\in {\mathcal{R}}^{n\times n}$和$W_{struc}^{(p,l)}\in {\mathcal{R}}^{n\times d_{struc}}$是可训练权重，捕捉边的权重和特征的重要性；也就是说，权重越大，对应的特征就越重要。为每个多项式和每个parts的图引入权重。注意，对于度normalization,图转移矩阵${\hat{A}}^{(p)}$提供了很好的边权重初始化，图转移矩阵稳定了$M_{struc}^{(p,l)}$的学习。当$L=1$，SGC退化为原始的空间图卷积运算。当$L>1$，SGC的作用类似于Chebyshev滤波器，并且能够逼近在图谱域中设计的卷积。

4.3. Actional-Structural Graph Convolution Block(动作结构图卷积块)

  为了完整地捕捉任意关节之间的动作结构特征，我们将AGC和SGC结合，组合成为了动作结构图卷积(ASGC)。在4，5式中，我们分别从AGC和SGC得到每时每刻的联合特征。我们使用两者的凸组合(convex combination)²作为ASGC的响应。从数学角度分析，ASGC操作为：$$X_{out}=ASGC(X_{in})=X_{struc}+\lambda X_{act}\in {\mathcal{R}}^{n\times d_{out}},$$其中，$\lambda$是一个超参数，它权衡了结构特征和动作特征之间的重要性。在ASGC之后，可以进一步引入非线性激活函数ReLU($\cdot$)。
定理1动作结构图卷积是一种有效的线性运算；即$Y_1=ASGC(X_1)$和$Y_2=ASGC(X_2)$。然后，$a{Y}_1+b{Y}_2=ASGC(a{X}_1+b{X}_2),\forall a,b\in \mathcal{R}$。
  线性确保ASGC有效地保存来自结构和动作方面的信息；例如，当来自动作方面的响应更强时，它可以通过ASGC有效地反映出来。

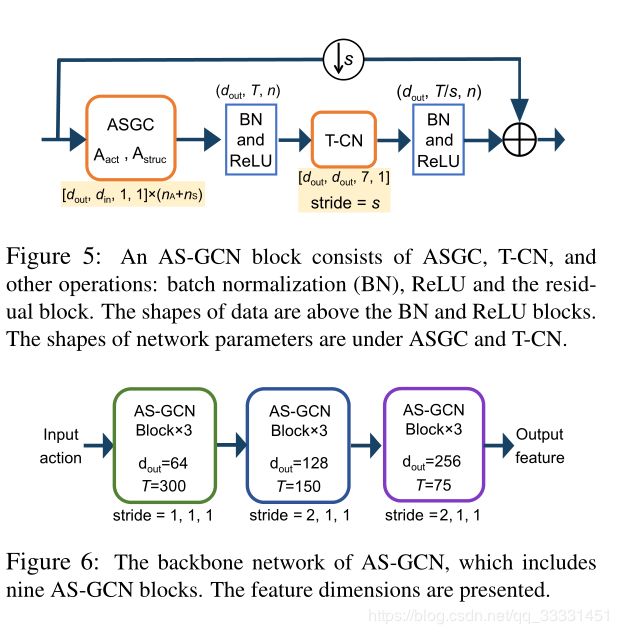
  为了捕捉帧间动作特征，我们在时间轴上使用一层时间卷积（T-CN），它独立地提取每个关节的时间特征，但在每个关节上共享权重。由于ASGC和T-CN分别学习空间和时间特征，我们将这两个层连接为动作结构图卷积块（AS-GCN块），以从各种动作中提取时间特征；参见图5。注意，ASGC是只提取空间信息的单个操作，AS-GCN块包括一系列提取空间和时间信息的操作。

4.4. Multitasking of AS-GCN(AS-GCN的多任务处理)

 骨架网(backbone network).我们堆叠一系列AS-GCN块作为骨干网络，称为AS-GCN；见图6。经过多个时空特征聚合后，AS-GCN跨时间提取高层语义信息。
 动作识别头(Action recognition head).为了对行为分类，我们在backbone network之后构造了一个识别头。我们在backbone network的特征映射输出的关节点和时间维度上使用全局平均池化，之后得到特征向量，最后将其输入到softmax分类器中，得到预测的类标签$\hat{y}$。动作识别的损失函数是标准的交叉熵损失函数$$\mathcal{L}=-y^T\log (\hat{y}),$$其中y是动作的真实标签。
 未来姿势预测头(Future pose prediction head)以往对骨架数据的分析大多集中在分类任务上。这里我们还考虑了姿态预测；也就是说，使用AS-GCN预测基于历史骨骼动作的未来三维关节位置。
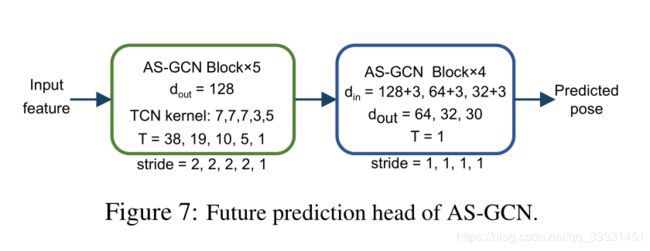
  为了预测未来的姿态，我们构建了一个预测模块，然后是backbone network。我们使用多个ASGCN块对从历史数据中提取的高级特征图进行解码，得到预测的未来3D关节位置$\hat{\mathcal{X}}\in {\mathcal{R}}^{n\times 3\times T^{\prime }}$；见图7。未来预测的损失函数是标准的$\mathcal{L}2$损失函数$${\mathcal{L}}_{predict}=\frac{1}{nd{T}^{\prime }}\sum _{i=1}^{nd}\sum _{t=1}^{T^{\prime }}||{\hat{\mathcal{X}}}_{i,:,t}-{\mathcal{X}}_{i,:,t}|{|}_2^2.$$
 **Joint model.**在实际应用中，当我们同时训练识别头和未来预测头时，识别性能得到了提高。算法原理是，未来预测模块促进自我监督，避免识别过拟合。

5. Experiments

5.1. Data sets and Model Configuration

5.2. Ablation Study

6、Conclutions

  提出了基于骨架的动作识别的动作结构图卷积网络（AS-GCN）。A-link推理模块捕获动作依赖项。我们还扩展了骨架图来表示高阶关系。为了更好地表示动作，将广义图反馈到ASGCN块。另一个未来姿势预测头通过自我监督捕捉更详细的模式。利用NTU-RGB+D和kinetics两个数据集验证了AS-GCN在动作识别中的有效性。与以前的方法相比，AS-GCN有了很大的改进。此外，AS-GCN也显示出对未来姿态预测有希望的结果。
后续更新中。。。

---

1. 【一文学会】Gumbel-Softmax的采样技巧 ↩︎

2. 凸组合 ↩︎