Multi-task中的多任务loss平衡问题

背景

multi-task的损失函数:
$$L(t)=\sum w_i(t)L_i(t,\theta )$$
在multi-task训练中存在着:

1. 如何平衡各个任务损失的权重,
2. 对于不同的任务的loss梯度之间的大小关系如果平衡,
3. 各任务学习率如何控制.

这些问题影响mult-task训练的最终效果. 处理不当, 很有可能一个task学的很好, 其他task学的很差.
三个问题是相通的.

7 Nov 2017 - GradNorm: Gradient Normalization for Adaptive Loss Balancing in Deep Multitask Networks

论文地址
GradNorm的解决方法, 将$w_i$作为可学习的参数.
目标是:

1. 在不考虑学习率的情况下, 尽量使得各个task的$w_i(t)L_i(t,\theta )$对于参数$\theta$的gradient都与平均值接近.
2. 学习不充分的task, 给与比其他task更大的学习率.

$t$时间task $i$的$\theta$梯度:
$$G_{\theta }^{(i)}(t)=\Vert {▽}_{\theta }{w}_i(t)L_i(t,\theta ){\Vert }_2$$
所有task对$\theta$的平均梯度:
$${\overline{G}}_{\theta }(t)=E_{task}[G_{\theta }^{(i)}(t)]$$
对于学习率, 定义若干个变量:
定义一个loss相对于初始化时的占比, 优化程度.
$$L_i(t)=L_i(t)/L_i(0)$$
定义一个比率值, 衡量task $i$相对于所有task的优化程度. 值越大, 表明优化程度相对于其他task 优化程度不够.
$$r_i(t)=L_i(t)/E_{task}[L_i(t)]$$
最后定义一个损失函数, 用来作为$w_i$的优化目标函数:
$$L_{grad}(t;w_i(t))=\sum _i|G_{\theta }^{(i)}(t)-{\overline{G}}_{\theta }(t)\times [r_i(t){]}^{\alpha }{|}_1$$
每次求上式对$w_i$的导数时, 固定${\overline{G}}_{\theta }(t)\times [r_i(t){]}^{\alpha }$的值, 所求的对$w_i$的梯度用来更新$w_i$的值.在每次更新之后. 需要对$w_i$进行normalization, 使得:
$$\sum _i{w}_i(t)=T$$
$w_i$初始化时赋值为1, 即$w_i(0)=1$

19 May 2017 - Multi-Task Learning Using Uncertainty to Weigh Losses for Scene Geometry and Semantics

论文地址
方法比较简单, 假设也很合理:
如果是回归问题, $f^w(x)$为模型输出:
则假设label 似然概率$y$符合高斯分布:
$$p(y|f^w(x))=\mathcal{N}(f^w(x),{\sigma }^2)$$
如果是分类问题, 最终class $y$的概率为:
$$p(y|f^w(x))=softmax(f^w(x))$$

这里面的$y$可以为一个向量. 比如序列问题中.

多个task($K$个), 希望整体概率最大.
$$p(y_1,...,y_K|f^w(x))=p(y_1|f^w(x))\times ...\times p(y_K|f^w(x))$$
又:
如果是回归问题:
$$\log p(y|f^w(x)\propto -\frac{1}{2{\sigma }^2}\Vert y-f^w(x){\Vert }^2-{\log }^{\sigma }$$
如果是分类问题, $c\in C$, 假设$\hat{c}$为正确分类:
$$\log p(y=\hat{c}|f^W(x),\sigma )=\frac{1}{{\sigma }^2}{f}_{\hat{c}}^W(x)-\log \sum _{c}exp(\frac{1}{{\sigma }^2}{f}_c^W(x))$$
分类问题时, 还有一个用来简化优化目标的的近似替换, 具体见论文.

因此最终的log似然损失函数可以将分类和回归问题通过一个公式表达:
$$\log p(y_1|f^w(x))+...+\log p(y_K|f^w(x))$$

10 Oct 2018 - Multi-Task Learning as Multi-Objective Optimization

论文地址
这篇文章的效果声称能够赛过前两篇:
第三个是文中第二个方法.

基本的想法是, 寻找多目标优化的帕累托最优解.

帕累托最优的定义:

帕累托最优解不止一个:
如下图: 由$C\to A$ 或者由$C\to B$都是一个pareto optimize, 但A与B互相不是.


多任务的帕累托最优求解方法:
MGDA (multiple-gradient descent algorithm) 算法.

1. 第一个条件是对${\theta }^{sh}$求导.
2. 第二个条件是对${\theta }^t$求导.

这个算法参见论文:
Multiple-gradient descent algorithm (MGDA) for multiobjective optimization
但这边论文提出MGDA算法在面对神经网络的庞大参数时存在两个问题:

1. 对高纬度梯度不是很试用(not scale gracefully)
2. 需要对每个task计算梯度

所以本文提出了一种使用Frank-Wolfe-based optimizer的算法来处理这两个问题. 只需要一次backward explicit task-specific gradients 能计算出MGDA的一个上界, 使用这个上界, 能够得出帕累托最优的结果.

该文的方法

对于公式3, 如果是两个task:

有解析解为:

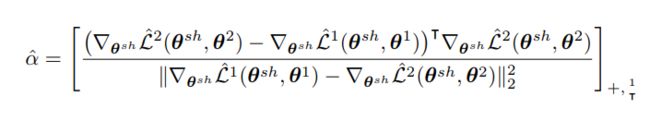
更一般的解法, 使用Frank wolfe 算法:

这个算法看的不是很懂, 可能需要看一下MGDA算法才能明白.

1. $e_{\hat{t}}$ 是什么.
2. 第10步和11步是怎么来的.
3. M矩阵从哪里冒出来的.

参考:

1. 原始frank wolfe算法