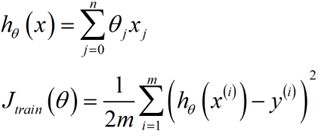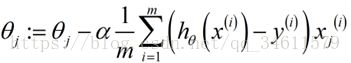吴恩达机器学习笔记（十七）-大规模机器学习
第十八章 大规模机器学习
学习大数据集
这一章中将讲述能够处理海量数据的算法。
思考：为什么要使用海量数据集呢？要知道获取高性能的机器学习系统途径是采用低偏差的学习算法，并用大数据进行训练。
这里拿之前提到过的易混淆词来举例，For breakfast I ate __ eggs，这里填two，而非too或者to，从下面的图中可以明确，只要使用大数据对算法进行训练，它的效果似乎会更好。
从这样的结果可以得出，在机器学习中，“It’s not who has the best algorithm that wins. It’s who has the mostdata.”，意思是决定因素往往不是最好的算法而是谁的训练数据最多。
但是大数据集有它自己的特殊的问题，即计算问题。假设有m等于一亿的训练样本，想要训练一个线性回归模型或一个逻辑回归模型，然后用梯度下降进行更新：
，可以看到其中计算梯度的项，当m等于一亿时，计算的代
价太大了，所以希望能找到替代这个算法的算法或寻找更有效的计算这项的方法，接下来，将介绍两个主要方法：随机梯度下降和减少映射，用来处理海量的数据集。
随机梯度下降
对很多机器学习算法，例如线性回归、逻辑回归和神经网络，推导算法的方法是提出一个代价函数或提出一个优化目标，然后使用梯度下降这样的算法求代价函数的最小值，但是当训练集很大时，使用梯度下降算法的计算量会变得非常大，接下来将讨论对梯度下降算法的改进：随机梯度下降法。
看一下之前提到的线性回归模型：
假设函数与代价函数如下：
使用梯度下降的公式如下：
那么当训练集很大时，用这样的梯度下降的更新，将会非常慢，花费的代价太大，下面来看一下更高效的算法，可以更好地处理大型数据集。
用另一种方式写出代价函数：
这个代价函数实际上是衡量假设函数在某个样本上的表现，所用总体的代价函数为：
用这种方法应用到线性回归模型上，写出随机梯度下降的过程：
▷ 随机打乱所有的数据集（随机打乱：将所有m个训练样本重新随机排列）；
▷ 对所有的训练样本进行遍历，进行更新：
，这一项其实是
；
所以随机梯度下降实际上是遍历所有的训练样本，首先是第一组训练样本
，此时只对第一个训练样本的代价函数进行梯度下降操作，然后把参数稍微修改一下，使其拟合的更好。然后以同样的方式继续操作后面的训练样本，直到完成整个训练集。
随机梯度下降不一样的地方在于不需要对全部m个样本求和来得到梯度项，只需要对单个训练样本求出这个梯度项，来看一下随机梯度下降过程的迭代过程:
总的来看，参数是朝着全局最小化的方向移动的，整个过程还是以随机迂回的路径朝着全局最小值前进，相比于普通梯度下降（红色的曲线），随机梯度下降的收敛形式是不同的，它所做的是连续不断在某个区域中朝着全局最小值方向徘徊。
Mini-Batch梯度下降
这一节中将会介绍Mini-Batch梯度下降，它有时比随机梯度下降法还要更快一些。
总结一下：
（1）普通梯度下降：每次迭代都要用到所有的m个样本；
（2）随机梯度下降：每次迭代只需用到一个样本；
（3）Mini-Batch梯度下降：它是介于上述两者之间，每次迭代会使用b个样本（b是称为Mini-Batch大小的参数，通常b的范围2-100）。
例如：假设b=10，得到10个样本为：
，然后进行梯度更新：
，接着再从i+10开始进行更新，一直进行下去，写下完整算法如下：
Mini-Batch梯度下降算法的缺点之一是要计算参数b的大小时，可能需要花费些时间，不过如果有优秀的向量化方法，有时它将比随机梯度下降运行的更快。
随机梯度下降收敛
这一节中将介绍确保算法的正确收敛以及调整随机梯度下降中的学习速率α的值。
回顾之前的普通梯度下降法，确保梯度下降已经收敛的一个标准方法就是绘制代价函数；而对于随机梯度下降，为了检查算法是否已经收敛，可以进行以下的工作：
▷ 沿用之前定义的代价函数：
▷ 当随机梯度下降法进行学习时，在使用某个样本
更新参数之前，可以计算出这个训练样本对应的假设表现有多好（即计算出代价函数）；
▷ 为了检查随机梯度下降是否收敛，要做的是每1000次迭代，就画出前一步中所计算出的代价函数，把这前1000个样本的代价函数的平均值画出来，通过观察所画的图，就能检查出随机梯度下降法是否在收敛。
下面是画出图的例子：
如果得到的上述这样的图，可以看出代价函数的值在下降，能够判断学习算法已经收敛了；
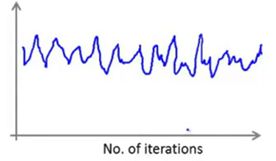
如果出现上述这样的情况，看起来代价函数完全没有在减小，似乎算法没有在进行学习
但是如果给出更多的训练样本求平均值，出现的曲线结果可能是如上图中红色的曲线所示，这样其实能看出代价函数是在减小的，只是求均值的样本太少的情况下，导致可能看不出实际上是趋向于减少的；
如果得到上图中这样的曲线，它看起来是在上升的，这样的情况就是算法发散的信号，这时要做的是用一个更小的学习速率α。
所以，通过上述所画的这些图，可以知道可能出现的各种情况，也能够应对不同的情况采取不同的措施。
最后，讨论说一下关于学习速率α的情况：
在大多数随机梯度下降法的典型应用中，学习速率α一般是一个不变的常数，因此最终得到的结果会在全局最小值附近徘徊，得到的是一个非常接近全局最小值的值。如果想让随机梯度下降更好地收敛到全局最小值，可以让学习速率α的值随时间变化逐渐减小。
一种典型的方法就是设置的值，让等于某个常数1除以迭代次数加上某个常数2（
），它的缺点是要确定两个常数的值需要花一些时间，但是如果能够找到这两个常数，得出的效果是很好的。
在线学习
这一节中将讨论一种新的大规模的机器学习机制：在线学习机制。
在线学习的案例：
假设你提供运输服务，用户们向你询问把包裹从A地运到B地的服务，同时假定你有一个网站，用户们登录网站告诉你他们想从哪里寄出包裹以及寄到哪里去，然后你的网站开出运输包裹的服务价格，根据你给用户的这个价格，用户有时会接受这个运输服务（y=1），有时候并不会接受（y=0），这里想要用一个学习算法帮助优化我们给用户开出的价格：
假设已经获取了描述用户特点的特征，比如用户的人口统计数据、用户邮寄包裹的起始地以及目的地，我们要做的是用这些特征学习用户将会用我们的运输服务来运输包裹的概率
，所以利用这些概率，就可以在新用户来的时候提供合适的价格。
考虑逻辑回归算法：假定有一个连续运行的网站，以下就是在线学习算法所做的：
如果真的运行一个大型网站，网站有连续的用户流，那么这种在线学习算法就非常适用。
另一个使用在线学习的例子：
这是一个产品搜索的应用，我们想要用一种学习算法来学习，如何反馈给用户好的搜索列表。假设有一个卖手机的店铺，有一个用户界面可以让用户登录你的网站并键入一个搜索条目，例如“安卓手机、1080p摄像头”，假定店铺中有100种手机，由于网站设计，当用户键入一个搜索命令，会找出10部合适的手机供用户选择。这里想要用一个学习算法帮助我们找到在这100部手机中哪10部手机是应该反馈给用户的。
接下来是解决问题的思路：
▷ 对于每个手机以及给定的用户搜索命令，可以构建特征向量x，这个特征向量可能会表示手机的各种特征，可能是：用户的搜索与这部电话的类似程度有多高、用户搜索命令中有多少词可以与这部手机的名字相配等等。
▷ 我们需要做的是估计用户点击某一手机链接的概率，所以将y=1定义为用户点击了手机的链接，而y=0是指用户没有点击链接，然后根据特征x来预测用户点击特定链接的概率
。
▷ 如果能够估计任意一个手机的点击率，可以利用这个来给用户展示10个他们最有可能点击的手机。
这就是在线学习机制，我们所使用的这个算法与随机梯度下降算法非常类似，唯一的区别就是不会使用一个固定的数据集，而是获取一个用户样本，从这个样本中学习，然后接着处理下一个，而且如果你的某个应用具有连续的数据流，在线学习机制非常值得考虑。
减少映射与数据并行
这一节中将讨论另一种可以应用在大规模机器学习上的思想：叫做MapReduce。
MapReduce的思想：
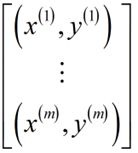
对于普通梯度下降法来说，假定有训练集如下：
根据MapReduce的思想，把训练集分割成不同的子集，假设m=400（这里为了方便介绍，实际处理大规模数据m应该是4亿的数量集），有4台机器可以处理数据，
第一台机器用前四分之一的训练集：
计算求和：
然后接着以此类推处理后面的训练集：
现在每个机器做的是四分之一的工作，使得它们能将原来的运行速度提高四倍，它们完成各自的temp计算后，然后把temp发给一个中心服务器去整合结果，最后更新参数：
。
下面是MapReduce的示意图：
如果想把MapReduce的思想应用在某种学习算法上，通过多台电脑并行计算来实现加速，思考：学习算法是否能表示成对训练集的一种求和？
实际上很多学习算法都可以表示成对训练集函数求和，而在大数据集上运行，所消耗的计算量就在于需要对非常大的训练集进行求和，所以只要学习算法可以表示为对训练集的求和，那么就可以用MapReduce将学习算法的使用范围扩展到非常大的数据集。
看下面的例子：
假设想要用一个高级的优化算法，比如L-BFGS、共轭梯度算法等等，假定要训练一个逻辑回归学习算法，需要去计算两个重要的量：
（1）计算优化目标的代价函数：
（2）高级优化算法需要偏导项的计算过程：
只要学习算法可以表示成一系列的求和形式或者表示在训练集上对函数求和的形式，就可以使用MapReduce技巧来并行化学习算法，使得其可以应用于非常大的数据集。
这就是利用MapReduce来实现数据的并行操作，能有效的提高运行效率，所以通过本章的学习，希望能够对大规模机器学习的方法有所了解和掌握。