决策树----ID3
由于这周国庆假期,所以学习就停了一段时间,毕竟放松放松也是挺好的,决策树是放假前看了一点,还没看完,所以先记记所看的内容。
还是继续机器学习实战的学习,相比较k-近邻算法而言,决策树能解决一些非数值的特征值分类问题,当然也能解决数值的特征值分类,这里我们所用的算法是ID3,ID3算法无法直接处理数值型数据,后面将学习CART(分类回归树)算法,则可以解决这个问题。那我们就提出问题了,一些数据的“内在含义”我们怎么获取呢?我们需要引进信息熵,我开始看见熵还以为是化学方程式中描述热量的信息量,大概就是信息增益,我也不是很懂为什么是这样定义,但是先用着吧。这里我曾产生了误解,以为信息量越大,信息熵越大,其实不然,这里有篇博客信息熵到底是什么?讲的还不错,吴军的数学之美里面也有讲到。
1.数学实现:
信息定义为:
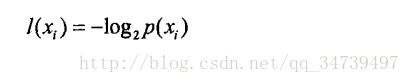
信息期望值定义:
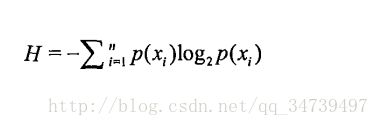
xi表示符号
p(xi)表示的是该分类出现的概率
这里不懂为什么这么定义没关系,我们只需要知道信息熵怎么计算就好。
2. 代码实现
- 计算信息熵
from math import log
import operator
def calcShannonEnt(dataSet):
numEntries = len(dataSet)
labelCounts = {}
for featVec in dataSet:
currentLabel = featVec[-1]
labelCounts[currentLabel] = labelCounts.get(currentLabel,0) + 1
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key])/numEntries
shannonEnt -= prob*log(prob,2)
return shannonEnt我们将公式转化成代码计算香农熵。
这里我们还是用 labelCounts[currentLabel] = labelCounts.get(currentLabel,0) + 1
字典类型来统计每个分类出现的频率,然后计算出现的概率prob
def createDataSet():
dataSet = [[1,1,'yes'],
[1,1,'yes'],
[1,0,'no'],
[0,1,'no'],
[0,1,'no']]
labels = ['不能浮出水面','是否有脚蹼']
return dataSet, labels这里我们创建数据集测试香农熵。
myDat,labels =trees.createDataSet()
print(myDat)
print(trees.calcShannonEnt(myDat))得出结果:

我们计算出了信息熵,这里我再加个分类,观察变化。

可以看到计算出的熵越大,数据越混乱,也就是数据分类越多。所以我们可以利用划分分类前后信息熵的变化来决定先用什么划分数据集。
2.根据信息熵划分最优类
def splitDataSet(dataSet,axis,value):#dataSet代表待划分的数据集,axis代表划分数据集的特征,value代表需要返回的特征值
retDataSet = []
for featVec in dataSet:
if featVec[axis] == value:
reducedFeatVec = featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSet这里按照输入的数据,划分数据集,返回划分的结果。
myDat,labels =trees.createDataSet()
print(myDat)
print(trees.splitDataSet(myDat,0,1))
print(trees.splitDataSet(myDat,0,0))我们来看看实验结果

这里我们用第一分类划分数据集,返回的0和1特征值的结果。
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1
baseEntropy = calcShannonEnt(dataSet)
bestInfoGain = 0.0
bestFeature = -1
for i in range(numFeatures):
featList = [example[i] for example in dataSet]
uniqueVals = set(featList)
newEntropy = 0.0
for value in uniqueVals:
subDataSet = splitDataSet(dataSet,i,value)
prob = len(subDataSet)/float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet)
infoGain = baseEntropy - newEntropy
if(infoGain > bestInfoGain):
bestInfoGain = infoGain
bestFeature = i
return bestFeature这里选取信息增益最大的划分数据集的方法,这里遍历了每种划分方式前后信息增益,选取最大信息增益作为第一个划分类。
这里我们还是用上面数据集做实验
myDat,labels =trees.createDataSet()
print(trees.chooseBestFeatureToSplit(myDat))
print(myDat)运行结果:

可以看到第0个特征是最好的划分,也即信息增益最大。
def majorityCnt(classList):
classCount={}
for vote in classList:
classCount[vote] = classCount.get(vote,0) + 1
sortedClassCount = sorted(classCount.iteritems(),key=operator.itemgetter(1),reverse=True)
return sortedClassCount[0][0]这个函数上一篇博客也有这个函数就是按序排序,然后选取第一个。
3.创建决策树
def createTree(dataSet,labels):
classList = [example[-1] for example in dataSet]
if classList.count(classList[0]) == len(classList):
return classList[0]
if len(dataSet[0]) == 1:
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet)
bestFeatLabel = labels[bestFeat]
myTree = {bestFeatLabel:{}}
del(labels[bestFeat])
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)#这里用了集合的唯一性
for value in uniqueVals:
subLabels = labels[:]
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet,bestFeat,value),subLabels)#递归调用
return myTree
这里倒数第二行递归调用一层层找出最佳划分方法然后存在字典里。当该分支下的节点所属的类别完全相同,即分类完成,也即都是叶子节点,就停止划分。但是如果我们分类已经划分完了,却还有类标签不是唯一的,我们这时可以采用多数表决方法(也就是 majorityCnt(classList)函数的功能)。
最后我们运行:
import trees
import treePlotter
myDat,labels=trees.createDataSet()
myTree = trees.createTree(myDat,labels)
print(myTree)得出结果:

由于放假,写的比较匆忙,等下会继续完善,后面还是要好好完成自己的学习任务0.0
这里我们就构建了我们第一个决策树了~0.0~
不过字典类型是不是有点丑,那我们就用matplotlib来画出来吧。
3. Matplotlib绘制树形图
Matplotlib提供了一个注解工具annotations,可以在数据图形上添加文本注释,这里我们先画个小例子。
先创建python模块treePlotter,然后将下列函数导入
#使用文本注解绘制树节点
import matplotlib.pyplot as plt
plt.rcParams['font.family']='SimHei'
decisionNode = dict(boxstyle="sawtooth", fc="0.8")#这里的文本框锯齿型,线宽0.8
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")
def plotNode(nodeTxt, centerPt, parentPt, nodeType):#nodeTxt代表文本内容,centerPt代表被指向坐标,parentPt代表起点坐标,nodeType就是文本框格式
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
xytext=centerPt, textcoords='axes fraction',
va="center", ha="center", bbox=nodeType, arrowprops=arrow_args )
def createPlot(inTree):
fig = plt.figure(1, facecolor='white')
fig.clf()
axprops = dict(xticks=[],yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
plotNode('决策节点', (0.5, 0.1), (0.1, 0.5), decisionNode)
plotNode('叶子节点', (0.8, 0.1), (0.3, 0.8), leafNode)
plt.show()import treePlotter
treePlotter.createPlot()我们已经知道怎么绘制树的节点了,但是节点的绘制位置是个问题。这里我们还需要知道树的深度和叶子节点的数目。
#获取叶节点的数目和树的层数
def getNumleafs(myTree):
numLeafs = 0
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':
numLeafs +=getNumleafs(secondDict[key])
else:
numLeafs+=1
return numLeafs
def getTreeDepth(myTree):
maxDepth = 0
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':
thisDepth = 1 + getTreeDepth(secondDict[key])
else:
thisDepth = 1
if thisDepth > maxDepth:maxDepth = thisDepth
return maxDepth这里我们通过递归判断子节点是否为字典类型,如果是则继续递归,否则加1。
然后我们加个字典决策树测试代码
def retrieveTree(i):
listOfTrees =[{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}},
{'no surfacing': {0: 'no', 1: {'flippers': {0: {'head': {0: 'no', 1: 'yes'}}, 1: 'no'}}}}
]
return listOfTrees[i]print(treePlotter.retrieveTree(1))
print(treePlotter.getTreeDepth(treePlotter.retrieveTree(1)))
print(treePlotter.getNumleafs(treePlotter.retrieveTree(1)))我们得到了树的叶子节点和树的深度后,现在就可以绘制树了,绘制树的代码还是比较复杂,需要自己一点点测试,慢慢理解,各个节点位置的计算也都是有规律可寻的。
#绘制决策树
def plotMidText(cntrPt,parentPt,txtString):#这里画两节点中间的文本
xMid = (parentPt[0] - cntrPt[0])/2.0 + cntrPt[0]
yMid = (parentPt[1] - cntrPt[1])/2.0 + cntrPt[1]
createPlot.ax1.text(xMid,yMid,txtString)
def plotTree(myTree, parentPt, nodeTxt):
numLeafs=getNumleafs(myTree)
depth = getTreeDepth(myTree)
firstStr = list(myTree.keys())[0]
cntrPt = (plotTree.xOff +(1.0 + float(numLeafs))/2.0/plotTree.totalW,plotTree.yOff)
plotMidText(cntrPt,parentPt,nodeTxt)
plotNode(firstStr, cntrPt, parentPt, decisionNode)
secondDict = myTree[firstStr]
plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':
plotTree(secondDict[key],cntrPt,str(key))
else:
plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff),cntrPt,leafNode)
plotMidText((plotTree.xOff,plotTree.yOff),cntrPt,str(key))
plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD
def createPlot(inTree):
fig = plt.figure(1, facecolor='white')
fig.clf()
axprops = dict(xticks=[],yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False,**axprops ) #
plotTree.totalW = float(getNumleafs(inTree))
plotTree.totalD = float(getTreeDepth(inTree))
plotTree.xOff = -0.5/plotTree.totalW
plotTree.yOff = 1.0
plotTree(inTree, (0.5,1.0), '')
plt.show()
这里我是用几个数据带进去测试的,慢慢的理解,有几点比较难理解:
1.cntrPt = (plotTree.xOff +(1.0 + float(numLeafs))/2.0/plotTree.totalW,plotTree.yOff)
1. plotTree.xOff = -0.5/plotTree.totalW
可以参考这篇文章机器学习数据挖掘机器学习实战决策树plotTree函数完全解析
运行下列代码
print(treePlotter.retrieveTree(1))
myTree = treePlotter.retrieveTree(1)
print(treePlotter.createPlot(myTree))4. 使用决策树预测隐形眼镜类型
最后,我们就以如何预测患者需要佩戴的隐形眼镜作为结尾吧。
lenses.txt
这是需要的文本数据,这里我稍微做了些中文修改。
import trees
import treePlotter
fr = open('lenses.txt',encoding='utf-8')
lenses = [inst.strip().split('\t') for inst in fr.readlines()]
lensesLabels=['年龄','处方','散光的','眼泪量']
lensesTree = trees.createTree(lenses,lensesLabels)
print(lensesTree)
treePlotter.createPlot(lensesTree)
trees.storeTree(lensesTree,'lensesTreeSto.txt')#这里执行序列化操作,可以在磁盘上保存对象
print(trees.grabTree('lensesTreeSto.txt'))
myDat,labels =trees.createDataSet()
print(trees.createTree(myDat,labels))运行结果如下:

可以看到眼睛的干涩还是湿润与镜片类型直接相关,以及年龄大的和年幼的一般不适合戴隐形眼镜,也很符合我们的常识。好了,总算完成了决策树算法,我们又学习了一个算法~0.0~


