【OpenCV图像处理】六、图像的傅里叶变换

众所周知，离散傅里叶变换（DFT）是数字信号处理的内容，在数字信号处理这门课程中，DFT处理的大多是一维的离散信号，它也是指傅里叶变换在时域和频域上都呈现出离散的形式。而在实际应用中，通常都是用FFT来进行高效的DFT计算。

而对于一幅图像，它是二维的信息，且存在空域中，对它进行DFT变换，可以理解为利用DFT处理二维的信号。在对图片进行了二维DFT后，变换的结果需要使用实数图像加虚数图像或是幅度图像加相位图像的形式，在大多数的实际图像处理过程中，对我们有作用的仅仅是幅度图像，因为它包含了原图像中几乎所有的几何信息成分，在频域中，对于一幅图像，高频的部分代表了图像的细节或是纹理等信息，低频的成分代表了图像的轮廓信息，如果我们对一幅细节众多的图像使用低通滤波器，那么它将失去所有的细节信息，这和信号处理中的滤波器原理是相同的。因此可以在频域内构造合适的滤波器来实现图像的增强和去噪，边缘检测，图像特征提取图像压缩等功能的实现。

在OpenCV中，实现图像DFT变换的方法比较容易，主要思想是利用几个函数的配合，最主要的函数如下：

dft(InputArray src, OutputArray dst, int flags=0, int nonzeroRows=0);

其中，第一个参数src是指输入矩阵，可以是实数或者虚数，第二个参数是指输出矩阵，函数调用后运算的结果存在这里。第三个参数是int类型的flags,代表的是转换的标识符，有默认值0，通过阅读OpenCV源码可知如下情况：

enum { DFT_INVERSE=1, DFT_SCALE=2, DFT_ROWS=4, DFT_COMPLEX_OUTPUT=16, DFT_REAL_OUTPUT=32,DCT_INVERSE = DFT_INVERSE, DCT_ROWS=DFT_ROWS };

最后的两个取值与DCT相关，在这里暂时先不加以讨论，只看前几个参数的意义：

DFT_INVERSE：用1维或2维的逆变换来代替默认的正向变换。

DFT_SCALE：缩放比例标识符，输出的结果都会以1/N进行缩放,通常会结合DFT_INVERSE一起使用。

DFT_ROWS：对输入矩阵每行进行正向或者反向的变换，可以在处理多种矢量的时候用于减小资源开销，常常是三维或高位变换等复杂操作。

DFT_COMPLEX_OUTPUT：进行一维或二维实数数组正变换，这样的可过虽然是复数阵列，但是拥有复数的共轭对称性，所以可以被写成一个拥有同样尺寸的实数阵列。

DFT_REAL_OUTPUT：进行一维或二维复数数组反变换，这样的结果通常是一个大小相同的复矩阵。如果输入的矩阵有复数的共轭对称性，便会输出实矩阵。

dft函数的第四个参数是int类型的nonzeroRow，拥有默认值0，当这个参数设置为非0值时，（最好是取值为想要处理的那一行）函数会假设只有输入矩阵的第一个非零行包含非零元素(没有设置DFT_INVERSE)或只有输出矩阵的第一个非零行包含非零元素（设置了DFT_INVERSE）这样的话，可以更高效的对其他行进行处理，以此可以用来节省时间开销，在计算DFT矩阵卷积的时候尤其有效。

下面再介绍几个在DFT变换函数中会用到的几个函数：

int getOptimalDFTSize(int vecsize);

这个函数返回给定的向量尺寸的傅里叶最优尺寸的大小，这是为了可以使用FFT来加速计算DFT，因此需要扩充图像，而至于扩充多少，就要由这个函数来得到。

void copyMakeBorder( InputArray src, OutputArray dst,int top, int bottom, int left, int right,int borderType, const Scalar& value=Scalar() );

这个函数的作用的扩充已知图像的边界。

函数的第一个参数和第二个参数分别是输入图像和输出图像，需要注意的是输出图像应该具有和输入图像一样的尺寸和数据类型。接下来的四个参数分别是指在四个方向上要扩充多少像素，第七个参数是指添加的边界类型，常见的取值是BODER_CONSTANT，也就是用常数进行添加，最后一个参数是const Scalar &类型的参数，拥有默认值0，当上一个参数取BORDER_CONSTANT时，这个参数就是边界的值。

void magnitude(InputArray x, InputArray y, OutputArray magnitude);

第一个坐标和第二个坐标分别代表了实部和虚部，第三个参数是输出的幅值，它和第一个参数拥有同样的尺寸和类型。

void normalize(InputArray src,OutoutArray dst,double alpha =1,double beta = 0,int norm_type=NORM_L2,int dtype=-1,InputArray mask=noArray());

函数的作用是对图像进行归一化处理，第一个参数和第二个参数分别是输入图像和输出图像，其中输出图像和原图像拥有一样的尺寸和类型。第三个参数alpha，指的是归一化后的最大值，有默认值1，第四个参数是double类型的beta，归一化后的最大值，有默认值0，第五个参数是int类型的norm_type，指的是归一化的类型，拥有默认值NORM_L2，第六个参数是dtype,拥有默认值-1，当这个值是负数时，输出矩阵和src拥有同样的类型，否则它和src拥有同样的通道数。最后一个参数是可选的掩膜操作，有默认值noArray();

最后给出利用上面的函数进行一幅图像的DFT变换的小程序：

声明：这部分程序参考了 浅墨（毛星云）编写的OpenCV3编程入门中的相关内容，相关版权无条件归原作者所有。

//实现图像的DFT变换

#include 
#include 
#include 
#include 

using namespace std;
using namespace cv;

int main()
{
	//以灰度模式读取图像并进行显示
	Mat srcImage = imread("2345.jpg", 0);
	if (!srcImage.data)
	{
		cout << "读入图像有误，请检查文件" << endl;
		return false;
	}
	imshow("原始图像", srcImage);

	//将输入图像拓展到最佳的尺寸，边界使用0进行补充
	int m = getOptimalDFTSize(srcImage.rows);
	int n = getOptimalDFTSize(srcImage.cols);
	//将添加的像素初始化为0
	Mat padded;
	copyMakeBorder(srcImage, padded, m - srcImage.rows, 0, n - srcImage.cols, 0, BORDER_CONSTANT, Scalar::all(0));

	//为傅里叶变换的结果分配存储空间(分为实部和虚部)
	//将planes数组合并成为一个多通道的数组complexI
	Mat planes[] = { Mat_(padded), Mat::zeros(padded.size(), CV_32F) };
	Mat complexI;
	merge(planes, 2, complexI);

	//就地进行离散傅里叶变换
	dft(complexI, complexI);

	//将负数转换为幅值，即为：log(1+sqrt(Re(DFT(I))^2+Im(DFT(I))^2))
	split(complexI, planes);	//将多通道数组分为两个单通道数组
								//planes[0] = Re(DFT(I)),planes[1] = Im(DFT(I))
	magnitude(planes[0], planes[1], planes[0]);
	Mat MagnitudeImage = planes[0];

	//进行对数尺度放缩
	MagnitudeImage += Scalar::all(1);
	log(MagnitudeImage, MagnitudeImage);	//求自然对数

	//剪切和重新分布幅度图的象限
	//若有奇数行和奇数列，进行频谱剪裁
	MagnitudeImage = MagnitudeImage(Rect(0, 0, MagnitudeImage.cols &-2, MagnitudeImage.rows &-2));
	//这句中的 & -2 是位操作，因为-2的二进制为除最后一位为0外其余均为1，因此与之后的结果为将最低位的1与掉
	//实现将原来的奇数变为偶数
	
	//重新排列傅里叶图像中的象限，使得原点位原图像中心
	int cx = MagnitudeImage.cols / 2;
	int cy = MagnitudeImage.rows / 2;
	Mat q0(MagnitudeImage, Rect(0, 0, cx, cy));		//ROI区域的左上方
	Mat q1(MagnitudeImage, Rect(cx, 0, cx, cy));	//ROI区域的右上方
	Mat q2(MagnitudeImage, Rect(0, cy, cx, cy));	//ROI区域的左下方
	Mat q3(MagnitudeImage, Rect(cx, cy, cx, cy));	//ROI区域的右下方

	//交换象限，左上与右下交换
	Mat tmp;
	q0.copyTo(tmp);
	q3.copyTo(q0);
	tmp.copyTo(q3);
	//交换象限，右上与左下进行交换
	q1.copyTo(tmp);
	q2.copyTo(q1);
	tmp.copyTo(q2);

	//归一化，用0~1之间的浮点数将矩阵变换为可视图的格式
	normalize(MagnitudeImage, MagnitudeImage, 0, 1, CV_MINMAX);

	//显示效果图
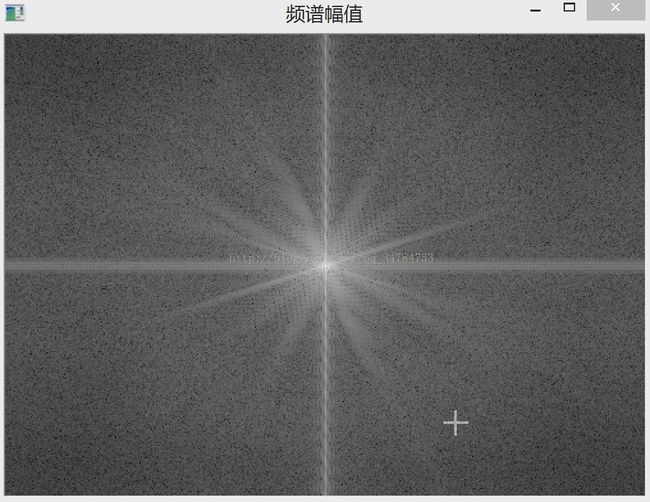
	imshow("频谱幅值", MagnitudeImage);

	waitKey();
	return 0;
}

程序执行后，输出的效果为：