线性回归原理分析
1 回归问题定义
线性回归是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。
回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。 如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析
回归问题的一般表达式为
(1.1) f ( x ) = θ 1 x 1 + θ 2 x 2 + . . . + θ d x d + b f(x) = \theta_1x_1 + \theta_2x_2 + ...+ \theta_dx_d + b \tag{1.1} f(x)=θ1x1+θ2x2+...+θdxd+b(1.1)
用向量形式写作
(1.2) f ( x ) = θ T x + b f(x) = \theta^Tx + b\tag{1.2} f(x)=θTx+b(1.2)
其中θ =(θ 1;θ 2;…;θ d),θ 与b确定后,这个线性模型就得以确定,我们则通过这个模型来预测数据,所以我们的目的就是去修改θ 和b的值,好让模型的预测值尽可能的与真实值一样。
2 问题求解
2.1目标函数引出
假设我们有m个样本,对于每个样本我们的预测值与误差的关系为
(2.1) y ( i ) = θ T x ( i ) + ϵ ( i ) y^{(i)} = \theta^Tx^{(i)} + \epsilon^{(i)} \tag{2.1} y(i)=θTx(i)+ϵ(i)(2.1)
其中 ϵ 为误差值,该误差 ϵ (i)是独立并且具有相同的分布,且服从均值为0方差为θ2的高斯分布,所以有
(2.2) p ( ϵ ( i ) ) = 1 2 π δ e x p ( − ( ϵ ( i ) ) 2 2 δ 2 ) p(\epsilon^{(i)}) = \frac{1}{\sqrt{2\pi}\delta}exp\left(-\frac{(\epsilon^{(i)})^2}{2\delta^2}\right)\tag{2.2} p(ϵ(i))=2πδ1exp(−2δ2(ϵ(i))2)(2.2)
将式2.1代入式2.2即有
(2.3) p ( y ( i ) ∣ x ( i ) ; θ ) = 1 2 π δ e x p ( − ( y ( i ) − θ T x ( i ) ) 2 2 δ 2 ) p(y^{(i)}|x^{(i)};\theta) = \frac{1}{\sqrt{2\pi}\delta}exp\left(-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\delta^2}\right)\tag{2.3} p(y(i)∣x(i);θ)=2πδ1exp(−2δ2(y(i)−θTx(i))2)(2.3)
于是得到似然函数
(2.4) L ( θ ) = ∏ i = 1 m 1 2 π δ e x p ( − ( y ( i ) − θ T x ( i ) ) 2 2 δ 2 ) L(\theta) = \prod_{i=1}^m\frac{1}{\sqrt{2\pi}\delta}exp\left(-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\delta^2}\right)\tag{2.4} L(θ)=i=1∏m2πδ1exp(−2δ2(y(i)−θTx(i))2)(2.4)
似然函数的意思就是我们取什么样的参数和我们的数据组合后恰好为真实值,为了让真实值和我们模型的预测值之间的误差最小,因此我们要让L(θ)最大。接下来对L(θ)表达式进行化简。为了方便计算,先对式2.4两边取log。
(2.5) l o g L ( θ ) = ∑ i = 1 m l o g 1 2 π δ e x p ( − ( y ( i ) − θ T x ( i ) ) 2 2 δ 2 ) = m l o g 1 2 π δ − 1 2 ∑ i = 1 m ( y ( i ) − θ T x ( i ) ) 2 \begin{aligned} logL(\theta) &= \sum_{i=1}^m log\frac{1}{\sqrt{2\pi}\delta}exp\left(-\frac{(y^{(i)}-\theta^Tx^{(i)})^2}{2\delta^2}\right)\\ &=mlog\frac{1}{\sqrt{2\pi}\delta} - \frac{1}{2}\sum_{i=1}^m(y^{(i)}-\theta^Tx{(i)})^2\\ \tag{2.5} \end{aligned} logL(θ)=i=1∑mlog2πδ1exp(−2δ2(y(i)−θTx(i))2)=mlog2πδ1−21i=1∑m(y(i)−θTx(i))2(2.5)
(2.6) 令 J ( θ ) = 1 2 ∑ i = 1 m ( y ( i ) − θ T x ( i ) ) 2 最小二乘法 \text{令}J(\theta) = \frac{1}{2}\sum_{i=1}^m(y^{(i)}-\theta^Tx{(i)})^2\text{ 最小二乘法}\tag{2.6} 令J(θ)=21i=1∑m(y(i)−θTx(i))2 最小二乘法(2.6)
从式2.5和2.6即可看出,为了让L(θ)最大,只需要让式2.6最小即可
2.2 目标函数求解
经过一系列的分析,我们已经得到我们的目标函数
(2.7) J ( θ ) = 1 2 ∑ i = 1 m ( y ( i ) − θ T x ( i ) ) 2 = 1 2 ( X θ − y ) T ( X θ − y ) \begin{aligned} J(\theta) &= \frac{1}{2}\sum_{i=1}^m(y^{(i)}-\theta^Tx{(i)})^2\\ &=\frac{1}{2}(X\theta-y)^T(X\theta-y)\\\tag{2.7} \end{aligned} J(θ)=21i=1∑m(y(i)−θTx(i))2=21(Xθ−y)T(Xθ−y)(2.7)
我们需要找到一组θ来让目标函数取到最小值,又因为目标函数连续,所以这组θ一定为目标函数的驻点。此时,我们对目标函数求导
(2.8) ∇ θ J ( θ ) = ∇ θ ( 1 2 ( X θ − y ) T ( X θ − y ) ) = 1 2 ( 2 X T X θ − X T X − ( y T X ) T ) = X T X θ − X T y \begin{aligned} \nabla_\theta J(\theta) &= \nabla_\theta \left(\frac{1}{2}(X\theta-y)^T(X\theta-y)\right)\\ &=\frac{1}{2}\left(2X^TX\theta-X^TX-(y^TX)^T\right)\\ &=X^TX\theta - X^Ty\\\tag{2.8} \end{aligned} ∇θJ(θ)=∇θ(21(Xθ−y)T(Xθ−y))=21(2XTXθ−XTX−(yTX)T)=XTXθ−XTy(2.8)
令偏导等于0,最终我们得到参数θ的解析式
(2.9) θ = ( X T X ) − 1 X T y \theta = (X^TX)^{-1}X^Ty\tag{2.9} θ=(XTX)−1XTy(2.9)
def standRegres(xArr,yArr):
xMat = mat(xArr);yMat = mat(yArr).T
xTx = xMat.T * xMat
#判断矩阵是否可逆
if linalg.det(xTx) == 0.0:
print("This Matrix is singular,cannot do inverse")
return
#得到解析解
theta= xTx.I*(xMat.T*yMat)
return theta
从上面实现代码可以看出,如果 ( X T X ) − 1 (X^TX)^{-1} (XTX)−1不可逆则无法计算,那怎么办呢?
这时我们需要引入岭回归的概念,简单来说岭回归就是在矩阵XTX上加上一个 λ I \lambda I λI从而使得矩阵非奇异,进而能对 X T X + λ I X^TX+\lambda I XTX+λI求逆。此时参数 θ \theta θ的解析式为
(2.10) θ = ( X T X + λ I ) − 1 X T y \theta = (X^TX+\lambda I)^{-1}X^Ty\tag{2.10} θ=(XTX+λI)−1XTy(2.10)
def ridgeRegres(xMat,yMat,lam=0.2):
xTx = xMat.T * xMat
#加上λI 从而使得矩阵非奇异
denom = xTx + eye(shape(xMat)[1])*lam
theta = denom.I * (xMat.T*yMat)
return theta
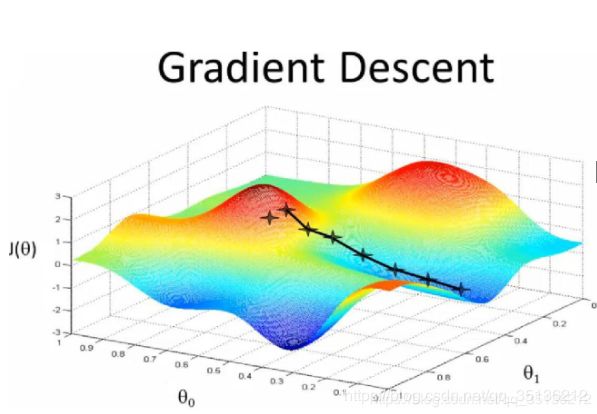
2.3 梯度下降法
我们在2.2节中论述的 θ \theta θ解析解只适用于参数维数不大的情况,当参数维度过大,再使用这种方法就不合适了,所以我们使用另外一种方法:梯度下降算法。
2.3.1 梯度下降算法步骤
(2.11) J ( θ ) = 1 2 ∑ i = 1 m ( y ( i ) − θ T x ( i ) ) 2 J(\theta) = \frac{1}{2}\sum_{i=1}^m(y^{(i)}-\theta^Tx{(i)})^2\tag{2.11} J(θ)=21i=1∑m(y(i)−θTx(i))2(2.11)
初始化theta,再沿着负梯度方向多次迭代更新 θ \theta θ每次选择一个更好的,直至收敛,最后可得到一个局部最优解。
(2.12) θ = θ − α δ J ( θ ) δ θ \theta = \theta - \alpha\frac{\delta J(\theta)}{\delta \theta}\tag{2.12} θ=θ−αδθδJ(θ)(2.12)
式中 α \alpha α表示学习率,学习率对结果会产生很大的影响,如果学习率设置过低则收敛速度很慢,如设置过高,则容易震荡难以收敛。
2.3.2 梯度下降算法分类
梯度下降算法根据每次迭代选择的样本数目不同可分为三类
- 批量梯度下降算法
每次迭代都考虑到所以样本,容易得到最优解,但是速度很慢
(2.13) δ J ( θ ) δ θ j = − 1 m ∑ i = 1 m ( y i − h θ ( x i ) ) x j i \frac{\delta J(\theta)}{\delta \theta_j} = -\frac{1}{m}\sum_{i=1}^m (y^i - h_\theta(x^i))x_j^i\\\tag{2.13} δθjδJ(θ)=−m1i=1∑m(yi−hθ(xi))xji(2.13)
θ j = θ j + 1 m ∑ i = 1 m ( y i − h θ ( x i ) ) x j i \theta _j = \theta _j + \frac{1}{m}\sum_{i=1}^m (y^i - h_\theta(x^i))x_j^i θj=θj+m1i=1∑m(yi−hθ(xi))xji
- 随机梯度下降算法
每次迭代只找一个样本,迭代速度很快,但不一定每次都朝着收敛的方向
(2.14) θ j = θ j + ( y i − h θ ( x i ) ) x j i \theta _j = \theta _j + (y^i-h_\theta (x^i))x_j ^i \tag{2.14} θj=θj+(yi−hθ(xi))xji(2.14)
- 小批量梯度下降算法
每次迭代从总数据中随机选择batch大小的数据进行计算,属于批量梯度下降和随机梯度下降的折中办法,比较实用。
θ j : = θ j − α 1 b a t c h S i z e ∑ k = i b a t c h S i z e ( h θ ( x ( k ) ) − y ( k ) ) x j ( k ) \theta _j :=\theta_j - \alpha\frac{1}{batchSize}\sum_{k=i}^{batchSize}(h_\theta(x^{(k)})-y^{(k)})x_j^{(k)} θj:=θj−αbatchSize1k=i∑batchSize(hθ(x(k))−y(k))xj(k)
#使用SGD
def trainSGD(self,X,Y,learningRate=1e-3,numIters=500,verbose=False):
xArray = np.array(X)
m,n= xArray.shape
if self.w is None:
self.w = np.ones(n)
lossHistory = []
for i in range(numIters):
dataIndex = list(range(m))
for j in range(m):
learningRate = 4/(1.0+j+i) + 0.01
randIndex = int(np.random.uniform(0,len(dataIndex)))
h = np.dot(xArray[randIndex],self.w.T)
loss = Y[0,randIndex] - h
lossHistory.append(loss)
self.w = self.w + learningRate*loss*X[randIndex]
del(dataIndex[randIndex])
if verbose and i%100 == 0:
print("迭代次数:%d/%d loss: %f"%(i,numIters,lossHistory[-1]))
return lossHistory
#使用BGD
def trainBGD(self,X,Y,learningRate=1e-3,reg=0.0,numIters=1000,verbose=False):
m,n = X.shape
xArray = np.array(X)
if self.w is None:
self.w = np.ones((n,1))
lossHistory = []
for i in range(numIters):
h = np.dot(xArray,self.w)
loss = Y[0].T-h
self.w = self.w + learningRate*np.dot(xArray.T,loss)
lossHistory.append(np.sum(loss))
if verbose and i%100==0:
print("迭代次数:%d/%d loss:%f"%(i,numIters,np.sum(loss)))
return lossHistory
代码点此获取GitHub