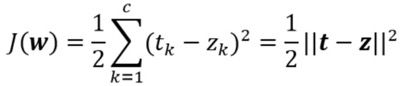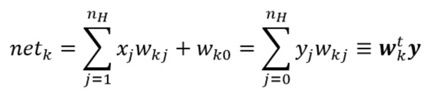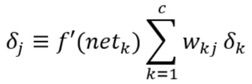BP神经网络细解——含代码，有详细说明，哈工大模式识别实验

我们以一个实验来说明整个流程，包括了数据生成，网络构建，网络训练，预测和最终验证。实验的要求如下：

---

一、实验计划

1.数据生成

采用np.random.multivariate_normal (mean, cov, size=None, check_valid=None, tol=None)方法，它用于生成多元正态分布矩阵。其中mean和cov为必要的传参而size，check_valid以及tol为可选参数。

2.网络结构定义，前向传播

网络采用3-3-4型BP网，即输入层为3，隐藏层为3，输出层为4，含偏置项，隐藏层激活函数采用ReLu，输出层采用softmax，loss函数J(W)采用均方差，如下所示，其中tk是实际标签，zk为网络估计的结果，c为样本的类别数。

3-3-4 BP网的结构如下图所示。由于输入为三维样本点，因此输入层为3；由于需要分为四类，因此输出层为4。中间隐藏层节点数和层数可随意组合，本实验设为3个。

前向传播较为简单，规则如下。xj是输入样本，wkj是权重矩阵，wk0是偏置值。

经过上式计算出输出后，经过激活函数得到如下结果。f为激活函数，本实验隐层采用ReLu，输出层采用softmax。

3.反向传播

该部分对于初学者是较难理解的部分，建议多花时间理解透彻，其实本质就是对loss函数求偏导，以达到降低loss就能优化网络的目的。偏导的求解过程读者可自行推导，对J(w)求导即可。最终得到权重的更新公式如下：

其中，wji是输入到隐藏层的权重，维度为3*3，wkj是隐藏层到输出的权重，维度为4*3。xi是输入样本，yj是隐藏层经过ReLu激活后的输出。det j和det k分别是隐层和输出层的敏感度。它们的定义如下，f'是softmax的偏导数。

4.预测

最后,经过softmax之后的输出,求其最大值所在的索引,将它作为预测的标签，具体规则是np.argmax(softmax(net k))。

---

二、实验过程

均方差的定义如下：

def mean_square(output, y):
    return np.sum((y - output) ** 2) / 2.0

softmax的定义如下：

def softmax(x):

    exps = np.exp(x - np.max(x))

    return exps / np.sum(exps)

ReLu函数的定义如下:

def ReLuFunc(x):

    x = (np.abs(x) + x) / 2.0

    return x

前向传播的定义如下:

# Hidden layer

for j in range(0, 3):

for i in range(0, 3):

net1[j] = net1[j] + w1[j][i] * x[i]

    net1[j] += bias1[j]

    fnet1 = ReLuFunc(net1)

     

# Output layer

for k in range(0, 4):

     for j in range(0, 3):

          net2[k] = net2[k] + w2[k][j] * fnet1[j]

     net2[k] += bias2[k]

 output = softmax(net2)

反向传播的定义如下:

# Back

det_k = np.zeros(4)

for k in range(0, 4):

     det_k[k] = (y[k] - output[k]) * (output[k] * (1 - output[k]))

det_j = np.zeros(3)

for j in range(0, 3):

     sum = 0

     for k in range(0, 4):

          sum = sum + w2[k][j] * det_k[k]

     if net1[j] >= 0:

          det_j[j] = sum

     else:

          det_j[j] = 0

               

# Update w and b

for j in range(0, 3):

    for i in range(0, 3):

        w1[j][i] = w1[j][i] + learning_rate * det_j[j] * x[i]

    bias1[j] = bias1[j] + learning_rate * det_j[j]

for k in range(0, 4):

     for j in range(0, 3):

         w2[k][j] = w2[k][j] + learning_rate * det_k[k] * fnet1[j]

     bias2[k] = bias2[k] + learning_rate * det_k[k]

准确率计算定义如下:

if np.argmax(output) == y:

    acc += 1

---

三、实验结果分析

1.数据生成

初始样本分布如图所示，可看到交叉较为严重，因此后面训练出来准确率也并不会太高，读者可自行调整u和sigma生成数据。

2.网络训练及测试集预测

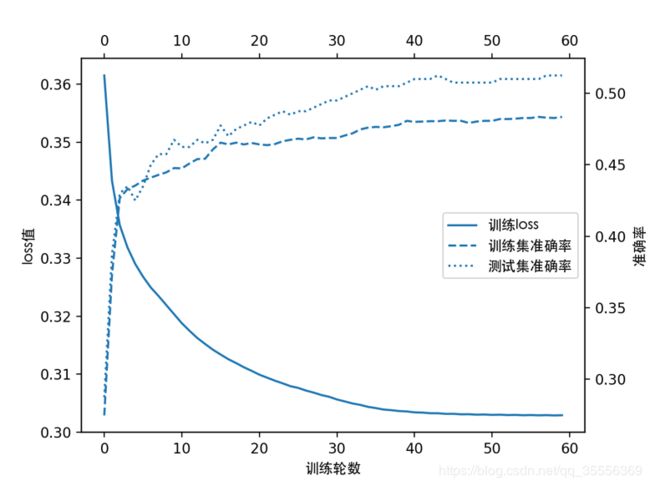
学习率设为0.01，每隔2轮降低为原来的0.97倍，每轮遍历所有的训练样本，得到结果图3所示。其中，最浅色的虚线是测试集400个样本的准确率随训练轮数的变化，最后稳定在51%左右。

3.给定样本预测

（1）网络预测

我们对实验第3题给出的5个样本进行预测，通过网络得到的结果如下，分别属于0、3、0、0、0类，而后是估计的后验概率。

（2）理论计算

该部分采用贝叶斯函数进行估计，先验概率为0.25，似然函数采用多维高斯分布概率密度函数，其公式定义如下：

具体计算的函数定义如下：

u = np.asarray([[0, 0, 0],
               [0, 1, 0],
               [-1, 0, 1],
               [0, 0.5, 1]])
sigma = np.asarray([[[1, 0, 0], [0, 1, 0], [0, 0, 1]],
                   [[1, 0, 1], [0, 2, 2], [1, 2, 5]],
                   [[2, 0, 0], [0, 6, 0], [0, 0, 1]],
                   [[2, 0, 0], [0, 1, 0], [0, 0, 3]]])
p = np.zeros(4)
for i in range(0, 4):
    det = np.linalg.det(sigma[i])
    inv = np.linalg.inv(sigma[i])
    xu_ = np.transpose(x - u[i])
    xu = np.transpose(xu_)
    first = np.dot(xu_, inv)
    second = np.dot(first, xu)
    d = len(x)
    p[i] = 1.0/((2*np.pi)**(d/2.0)*np.sqrt(det))*np.exp(-second/2.0)
prob = max(p)/np.sum(p)

得到结果如下：

对比网络预测结果如下表所示。可见，对5个样本的预测，BP网计算的结果是是03000，而理论计算的结果是00000，只有第2个样本的结果不一致，其他均相符。

样本数据	先验概率	理论后验概率(最大值)	理论结果(最大值对应类别)	预测后验概率	预测结果
(0,0,0)	0.25	0.57	0	0.51	0
(-1,0,1)	0.25	0.38	0	0.39	3
(0.5,-0.5,0)	0.25	0.61	0	0.55	0
(-1,0,0)	0.25	0.55	0	0.53	0
(0,0,-1)	0.25	0.50	0	0.36	0

项目github开源地址：https://github.com/HuiyanWen/BP_Network ，如果有用，请您点个赞，谢谢~