Leetcode-Java(十九)

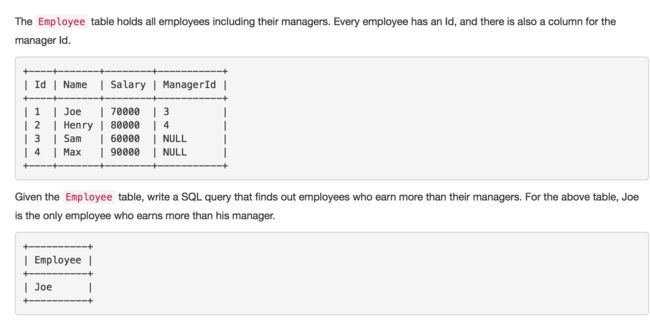
181. Employees Earning More Than Their Managers

# Write your MySQL query statement below
select 
    t1.Name as Employee
from
 (select * from Employee) t1
 inner join
 (select * from Employee) t2
 on t1.ManagerId = t2.Id
where t1.Salary > t2.Salary

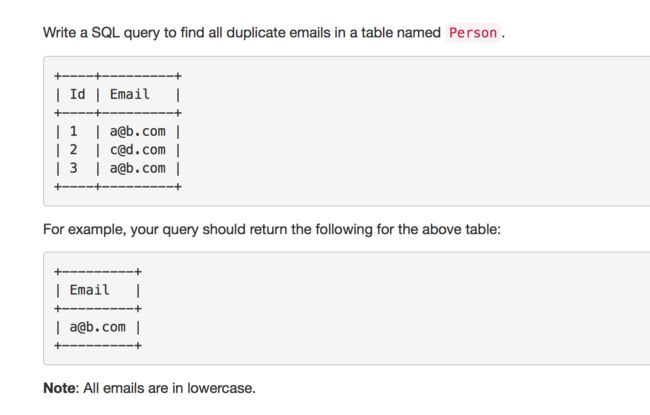
182. Duplicate Emails

# Write your MySQL query statement below
select
    Email
from
(
select 
    Email,count(*) as cnt
from
    Person
group by Email
) t
where cnt>1

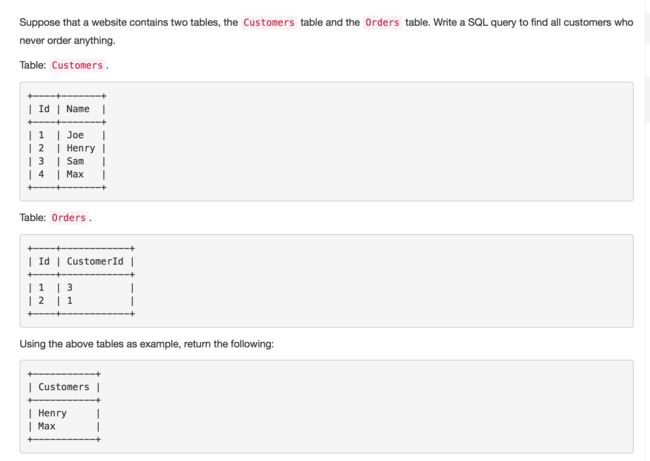
183. Customers Who Never Order

# Write your MySQL query statement below
select 
Name as Customers
from
(select * from Customers) t1
left join
(select CustomerId from Orders) t2
on t1.Id = t2.CustomerId
where t2.CustomerId is null

184. Department Highest Salary

# Write your MySQL query statement below
select
t3.Name as Department,t1.Name as Employee,t1.Salary
from
(select * from Employee) t1
inner join
(select DepartmentId,max(Salary) as Salary from Employee group by DepartmentId) t2
on t1.DepartmentId = t2.DepartmentId and t1.Salary = t2.Salary
inner join
(select * from Department) t3
on t1.DepartmentId = t3.Id

185. Department Top Three Salaries

如果是hive的话用row_number就能解决的问题，用mysql要好多子循环呀，心塞

# Write your MySQL query statement below
select 
    a2.Name as Department ,
    a1.EmployeeName as Employee,
    a1.Salary as Salary
from(
    select * from
(
select 
    t1.Name as EmployeeName,t1.Salary,t1.DepartmentId,count(distinct t2.Salary) as rank
from
(select * from Employee) t1
inner join
(select * from Employee) t2
on
t1.DepartmentId = t2.DepartmentId
where t1.Salary <= t2.Salary
group by t1.Name,t1.Salary,t1.DepartmentId
    ) a
    where a.rank <= 3
) a1
inner join
(select * from Department) a2
on
a1.DepartmentId = a2.Id
order by a2.Name,a1.Salary desc

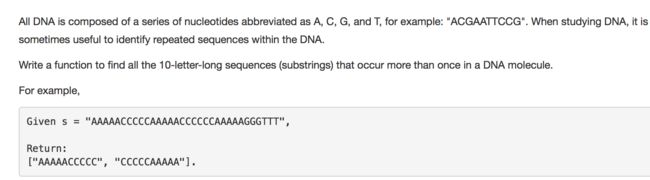
187. Repeated DNA Sequences

用一个HashMap保存出现过的字符串。

class Solution {
    public List findRepeatedDnaSequences(String s) {
        List res = new ArrayList();
        if(s==null || s.length()<=10)
            return res;
        Map map = new HashMap();
        for(int i=0;i

188. Best Time to Buy and Sell Stock IV

这道题是股票系列的第四题，在第三题的基础上变成了我们最多可以进行N次交易，本题的解法也适用于第三题，只需要将N设置为2就行了嘛。

首先，我们要确定的是，买和卖才算一次交易，而单独的买或者单独的卖不算一次交易。基于这个假定，如果k大于时间长度的一半的话，我们只需要简单的遍历数组，将第二天价格比前一天大的价格的差值累积求和就可以啦。

如果不是这样的话，我们在N天中进行K次交易有多种选择的话，我们可以维护两个数组，分别叫做global和local,我们用二维的数组来进行介绍，但是实际实现时可以使用一维的数组，因为我们是按天迭代的，类似这种情况的我们都可以将二维数组压缩成一维数组来减小空间复杂度。我们首先介绍一下两个数组的含义。
global[i][j]的含义是：在第I天最多进行j次交易，那么所能得到的最大的利润是什么。
local[i][j]的含义是：在第I天最多进行j次交易，并且最后一次交易是发生在第i天时所能得到的最好的利润。

根据这两个数组的含义，我们来讲解一下二者的递推公式，首先我们定义prices[i]-prices[i-1]即两天股票的差值为diff。那么对于global来说，global[i][j] = max(global[i-1][j],local[I][j])，即在最多进行j笔交易的情况下，最后一笔交易是否发生在今天，如果发生在今天所能获得的利润大的话，那么global[i][j] = local[i][j]，如果不是的话，则global[i][j]=global[i-1][j]。对于local来说，local[i][j] = max(local[i-1][j] + diff, global[i-1][j-1]+diff)。也就是看两个量，第一个是全局到i-1天进行j-1次交易，然后加上今天的交易，第二个量则是取local第i-1天j次交易，然后加上今天的差值（这里因为local[i-1][j]包含第i-1天卖出的交易，所以现在变成第i天卖出，并不会增加交易次数，而且这里无论diff是不是大于0都一定要加上，因为否则就不满足local[i][j]必须在最后一天卖出的条件了）。

好了，明确了上面的递推关系，我们可以写出如下的代码：

class Solution {
    public int maxProfit(int k, int[] prices) {
        if(prices==null || prices.length==0 || k<=0)
            return 0;
        int res = 0;
        if(k>=prices.length / 2){
            for(int i=0;i prices[I])
                    res += (prices[i+1] - prices[I]);
        }
        else{
            int[] global = new int[k+1];
            int[] local = new int[k+1];
            for(int i=0;i=1;j--){
                    local[j] = Math.max(local[j] + diff,global[j-1] + diff);
                    global[j] = Math.max(local[j],global[j]);
                }
            }
            res = global[k];
        }
        return res;
    }
}

189. Rotate Array

用多次reverse的思路，大家在纸上画一画就知道是怎么回事啦。

class Solution {
    public void rotate(int[] nums, int k) {
        if(nums==null || nums.length==0)
            return;
        k %= nums.length;
        reverse(nums,0,nums.length-1);
        reverse(nums,0,k-1);
        reverse(nums,k,nums.length-1);
        
    }
    public void reverse(int[] nums,int start,int end){
        while(start

190. Reverse Bits

public class Solution {
    // you need treat n as an unsigned value
    public int reverseBits(int n) {
        int result = 0;
        for (int i = 0; i < 32; i++) {
            result += n & 1;
            n >>>= 1;   // CATCH: must do unsigned shift
            if (i < 31) // CATCH: for last digit, don't shift!
                result <<= 1;
        }
        return result;
    } 
}