BZOJ 5384 有趣的字符串题（区间本质不同回文串数量）

题意：
多次求区间本质不同回文串数量。

我们知道区间本质不同子串个数是SAM+LCT+BIT。
所以区间本质不同回文串个数就是PAM+SegmentTree+BIT。
为什么可以搏一搏LCT变线段树呢？
因为PAM同时有着组合border的离谱性质。
套用区间本质不同子串个数的做法。
那么我们需要离线后移动右端点$R$，然后更新一系列PAM上的节点的最后一次出现的时间并且在BIT上维护关于$[L,R]$内的本质不同回文串个数。
考虑PAM上一条链，满足每个祖先都是后代的回文后缀，也就一定是border。
那么border就会满足可以拆分成log个长度呈等差数列的回文后缀。

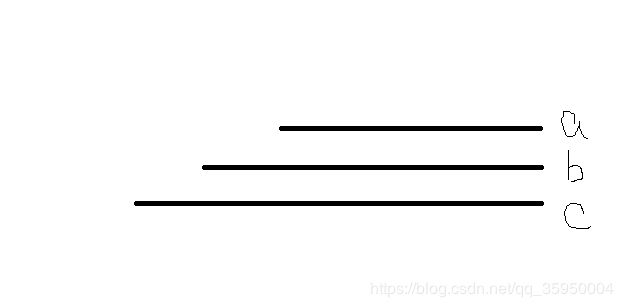
考虑上图三个等差回文后缀，我们更新$a$的最后一次出现的时间，实际上就是在BIT上给区间$[a最后一次出现的时间+1，当前时间-a的长度]$区间加一。
对于等差回文后缀可以发现，a最后一次出现的时间就是当前时间-b的长度。
所以上面的所有回文串abc通通可以化为 给区间$[c最后一次出现的时间+1，当前时间-a的长度]$区间加一。
而$c$最后一次出现的时间，可以在PAM上线段树合并就像维护right集合一样，也可以动态地单点修改，子树（区间）取$max$。（其实好像$SAM$也可以这样做。）
所以就每次暴力跳等差回文后缀即可。
$\mathcal{A}CCode$

#include
#define maxn 300055
#define maxm 1000005
#define rep(i,j,k) for(int i=(j),LIM=(k);i<=LIM;i++)
#define per(i,j,k) for(int i=(j),LIM=(k);i>=LIM;i--) 
#define mod 1000000007
#define maxc 26
using namespace std;
char cb[1<<16],*cs=cb,*ct=cb;
#define getc() (cs==ct&&(ct=(cs=cb)+fread(cb,1,1<<16,stdin),cs==ct)?0:*cs++)
void read(int &res){
	char ch;bool f=0;
	for(;!isdigit(ch=getc());) if(ch=='-') f= 1;
	for(res=ch-'0';isdigit(ch=getc());res=res*10+ch-'0');
	(f) && (res=-res);
}
int n,m;
char s[maxn]; 
int fa[maxn],len[maxn],tot,last,tr[maxn][maxc],l[maxm],r[maxm],anc[maxn],dif[maxn];
vector<int>G[maxn],E[maxn];
int sm[maxn],pos[maxn],sm2[maxn],ans[maxm];
#define pb push_back 

int st[maxn],ed[maxn],tim;
void dfs(int u){
	st[u] = ++tim;
	for(int v:E[u])
		dfs(v);
	ed[u] = tim;
}

namespace BIT{
	int tr[maxn];
	inline void upd(int u,int v){ for(;u<=n;u+=u&-u) tr[u] += v; }
	inline int qry(int u){ int r=0;for(;u;u-=u&-u) r += tr[u] ;return r; }
}

namespace Seg{
	int mx[maxn<<2];
	#define lc u<<1
	#define rc lc|1
	inline void ins(int u,int l,int r,int p,int v){
		if(l==r) return (void)(mx[u] = v);
		int m= l+r>>1;
		p <= m ? ins(lc,l,m,p,v) : ins(rc,m+1,r,p,v);
		mx[u] = max(mx[lc] , mx[rc]);
	}
	inline int qry(int u,int l,int r,int ql,int qr){
		if(l>qr||ql>r) return 0;
		if(ql<=l&&r<=qr) return mx[u];
		int m = l+r>>1;
		return max(qry(lc,l,m,ql,qr) , qry(rc,m+1,r,ql,qr));
	}
};

int main(){
	
	freopen("string.in","r",stdin);
	freopen("string.out","w",stdout);
	
	read(n),read(m);
	s[0] = '#';
	fa[0] = 1 , len[1] = -1 , tot = 1;
	last = 0;
	while(!isalpha(s[1] = getc()));
	rep(i,1,n){
		if(i > 1) s[i] = getc();
		int v= s[i] - 'a';
		for(;s[i] != s[i-len[last]-1];last = fa[last]);
		if(!tr[last][v]){
			int u = fa[last];
			for(;s[i] != s[i-len[u]-1];u = fa[u]);
			fa[++tot] = tr[u][v] , len[tot] = len[last] + 2;
			dif[tot] = len[tot] - len[fa[tot]];
			anc[tot] = (dif[tot] == dif[fa[tot]] ? anc[fa[tot]] : fa[tot]);
			tr[last][v] = tot;
		}
		last = tr[last][v];
		pos[i] = last;
	}
	rep(i,1,m){
		read(l[i]),read(r[i]);
		G[r[i]].pb(i);
	}
	rep(i,0,tot) if(i!=1) E[fa[i]].push_back(i);
	dfs(1);
	int ret = 0;
	rep(i,1,n){
		int u = pos[i];
		for(;u;u=anc[u]){
			BIT::upd(max(1,Seg::qry(1,1,n,st[u],ed[u])-len[u]+2),1);
			BIT::upd(i-len[anc[u]]-dif[u]+2,-1);
		}
		Seg::ins(1,1,n,st[pos[i]],i);
		for(int v:G[i])
			ret = (ret + 1ll * v * BIT::qry(l[v])) % mod; 
	}
	printf("%d\n",ret);
}