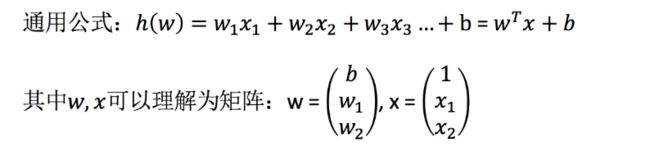人工智能入门课程学习（6）——线性回归

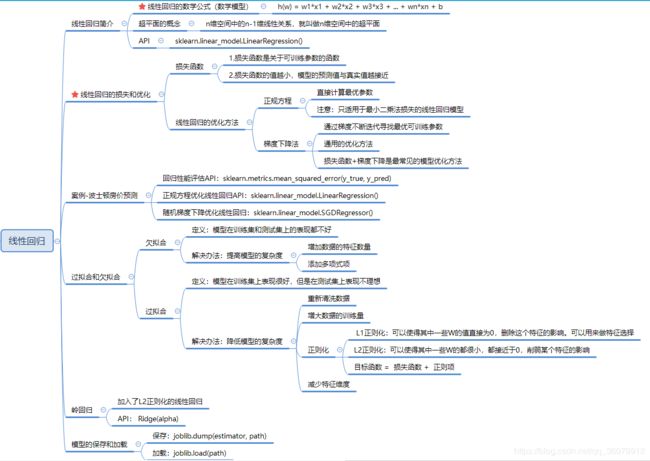
1.线性回归的简介

1.1 定义

线性回归(Linear regression)是利用回归方程(函数)对**一个或多个自变量(特征值)和因变量(目标值)**之间关系进行建模的一种分析方式。

特点：只有一个自变量的情况称为单变量回归，多于一个自变量情况的叫做多元回归

1.2 线性回归的应用场景

• 房价预测

• 销售额度预测

• 贷款额度预测

1.3 线性模型理解

举两个例子：

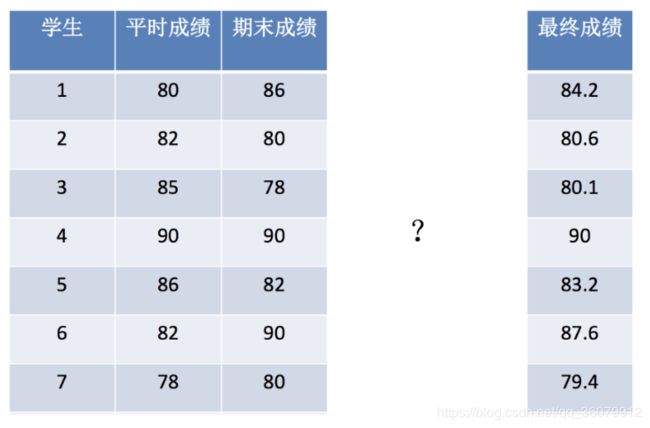
期末成绩：0.7×考试成绩+0.3×平时成绩
房子价格 = 0.02×中心区域的距离 + 0.04×城市一氧化氮浓度 + (-0.12×自住房平均房价) + 0.254×城镇犯罪率

上面两个例子，我们看到特征值与目标值之间建立了一个关系，这个关系可以理解为线性模型。

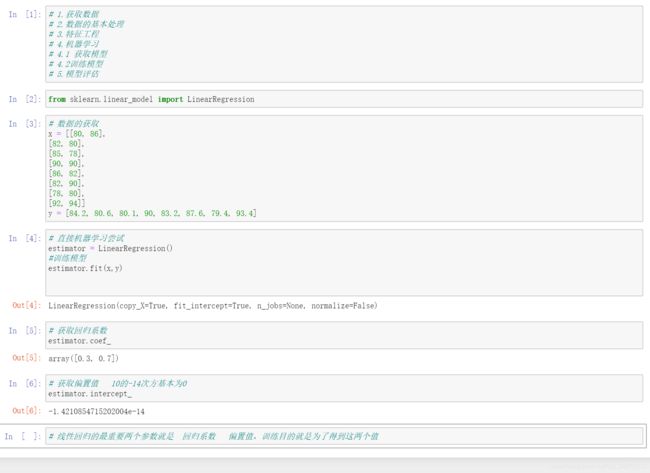
使用线性回归的API解决上边的期末成绩案例

线性回归API

sklearn.linear_model.LinearRegression()
LinearRegression.coef_：回归系数

解决的数据

代码实现

2.线性回归的损失与优化

在实际中，真实的回归系数与我们预测的回归系数可能截然不同，真实结果与预测结果之间的差值我们就用损失函数来表示。

2.1 损失函数

总损失定义为：


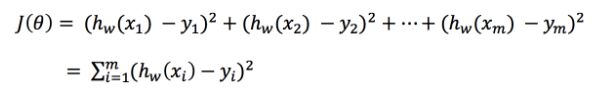
如何去减少这个损失，使我们预测的更加准确些？既然存在了这个损失，我们一直说机器学习有自动学习的功能，在线性回归这里更是能够体现。这里可以通过一些优化方法去优化（其实是数学当中的求导功能）回归的总损失！
很多时候对算法的优化就是在求在J(θ)取得最小值（极小值）的时候，对应的回归系数w的值
求J(θ)的极小值的时候常常会遇到局部最优问题，如何解决局部最优问题，找到全局的最优值是机器学习中的重点。

2.2 优化方法

常用的优化方法包括正规方程法和梯度下降法。两者的对比：


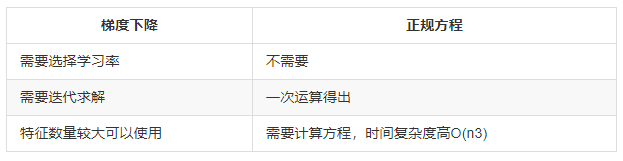
常用的梯度下降法：

• 全梯度下降算法(Full gradient descent）FG
• 随机梯度下降算法（Stochastic gradient descent）SG
• 随机平均梯度下降算法（Stochastic average gradient descent） SAG
• 小批量梯度下降算法（Mini-batch gradient descent） mini-bantch

3.scikit里边的线性回归api具体介绍

• sklearn.linear_model.LinearRegression(fit_intercept=True)
  • 通过正规方程优化
  • fit_intercept：是否计算偏置
  • LinearRegression.coef_：回归系数
  • LinearRegression.intercept_：偏置
• sklearn.linear_model.SGDRegressor(loss=“squared_loss”, fit_intercept=True, learning_rate =‘invscaling’, eta0=0.01)
  • SGDRegressor类实现了随机梯度下降学习，它支持不同的 loss函数和正则化惩罚项来拟合线性回归模型。
  • loss:损失类型
    • loss=”squared_loss”: 普通最小二乘法
  • fit_intercept：是否计算偏置
  • learning_rate : string, optional
    • 学习率填充
    • ‘constant’: eta = eta0
    • ‘optimal’: eta = 1.0 / (alpha * (t + t0)) [default]
    • ‘invscaling’: eta = eta0 / pow(t, power_t)
      - power_t=0.25:存在父类当中
      - 对于一个常数值的学习率来说，可以使用learning_rate=’constant’ ，并使用eta0来指定学习率。
  • SGDRegressor.coef_：回归系数
  • SGDRegressor.intercept_：偏置

sklearn提供给我们两种实现的API， 可以根据选择使用

4. 案例：波士顿放假预测

4.1 分析

回归当中的数据大小不一致，是否会导致结果影响较大。所以需要做标准化处理。

• 数据分割与标准化处理
• 回归预测
• 线性回归的算法效果评估

4.2 回归性能评估

均方误差(Mean Squared Error)MSE)评价机制：

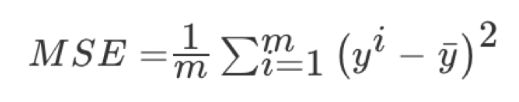
• sklearn.metrics.mean_squared_error(y_true, y_pred)
  • 均方误差回归损失
  • y_true:真实值
  • y_pred:预测值
  • return:浮点数结果

4.3 代码

1.使用标准的线性回归方法预测

# 1.导入数据 load_bostan
# 2.数据的基本处理 划分数据集
# 3.特征工程 标准化
# 4.机器学习 分别使用正规方程和梯度下降的方法来进行训练
# 5.模型评估 使用MSE 均方误差

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import SGDRegressor
from sklearn.metrics import mean_squared_error
from sklearn.linear_model import Ridge

## 线性回归方法预测

# 1.导入数据 load_bostan
data = load_boston()

# 2.数据的基本处理 划分数据集
x_train,x_test,y_train,y_test = train_test_split(data.data,data.target,test_size=0.2,random_state=20)

# 3.特征工程 标准化
# 3.1 初始化标准化转换器
transfer = StandardScaler()
# 3.2 转换数据
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

# 4.机器学习
# 4.1 正规方程解决
# 构建模型   初始化估计器
estimator = LinearRegression()
# 训练模型
estimator.fit(x_train,y_train)

# 5.模型评估  MSE
# 先求出预测值
y_predict = estimator.predict(x_test)
# 使用MSE 评估
mean_squared_error(y_pred=y_predict,y_true=y_test)

预测的结果为：

2.使用梯度下降法来预测

# 1.导入数据 load_bostan
data = load_boston()

# 2.数据的基本处理 划分数据集
x_train,x_test,y_train,y_test = train_test_split(data.data,data.target,test_size=0.2,random_state=20)

# 3.特征工程 标准化
# 3.1 初始化标准化转换器
transfer = StandardScaler()
# 3.2 转换数据
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

# 4.机器学习
# 4.1 梯度下降解决
# 构建模型   初始化估计器    设置迭代1000次停止，或者误差值小于0.001停止
estimator = SGDRegressor(max_iter=1000,tol=0.001)
# 训练模型
estimator.fit(x_train,y_train)

# 5.模型评估  MSE
# 先求出预测值
y_predict = estimator.predict(x_test)
# 使用MSE 评估
mean_squared_error(y_pred=y_predict,y_true=y_test)

5.欠拟合和过拟合

5.1 定义概述

• 过拟合：一个假设在训练数据上能够获得比其他假设更好的拟合， 但是在测试数据集上却不能很好地拟合数据，此时认为这个假设出现了过拟合的现象。(模型过于复杂)
• 欠拟合：一个假设在训练数据上不能获得更好的拟合，并且在测试数据集上也不能很好地拟合数据，此时认为这个假设出现了欠拟合的现象。(模型过于简单)
  
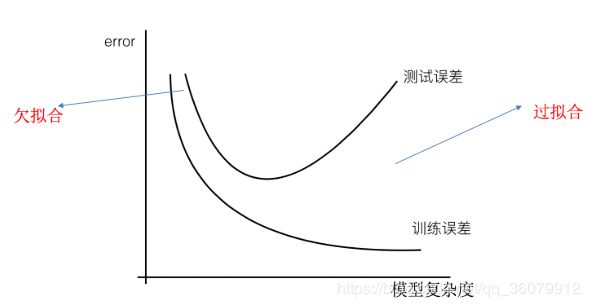
  线性回归进行训练学习的时候变成模型会变得复杂，这里就对应前面再说的线性回归的两种关系，非线性关系的数据，也就是存在很多无用的特征或者现实中的事物特征跟目标值的关系并不是简单的线性关系。

5.2 原因以及解决办法

• 欠拟合原因以及解决办法
  • 原因：学习到数据的特征过少
  • 解决办法：
    • 1）添加其他特征项，有时候我们模型出现欠拟合的时候是因为特征项不够导致的，可以添加其他特征项来很好地解决。例如，“组合”、“泛化”、“相关性”三类特征是特征添加的重要手段，无论在什么场景，都可以照葫芦画瓢，总会得到意想不到的效果。除上面的特征之外，“上下文特征”、“平台特征”等等，都可以作为特征添加的首选项。
    • 2）添加多项式特征，这个在机器学习算法里面用的很普遍，例如将线性模型通过添加二次项或者三次项使模型泛化能力更强。
• 过拟合原因以及解决办法
  • 原因：原始特征过多，存在一些嘈杂特征， 模型过于复杂是因为模型尝试去兼顾各个测试数据点
  • 解决办法：
    • 1）重新清洗数据，导致过拟合的一个原因也有可能是数据不纯导致的，如果出现了过拟合就需要我们重新清洗数据。
    • 2）增大数据的训练量，还有一个原因就是我们用于训练的数据量太小导致的，训练数据占总数据的比例过小。
    • 3）正则化
    • 4）减少特征维度，防止维灾难

6.线性回归的改进-岭回归

6.1 API引用

• sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True,solver=“auto”, normalize=False)

  • 具有l2正则化的线性回归
  • alpha:正则化力度，也叫 λ
    • λ取值：0~1 1~10
  • solver:会根据数据自动选择优化方法
    • sag:如果数据集、特征都比较大，选择该随机梯度下降优化
  • normalize:数据是否进行标准化
    • normalize=False:可以在fit之前调用preprocessing.StandardScaler标准化数据
  • Ridge.coef_:回归权重
  • Ridge.intercept_:回归偏置
    Ridge方法相当于SGDRegressor(penalty=‘l2’, loss=“squared_loss”),只不过SGDRegressor实现了一个普通的随机梯度下降学习，推荐使用Ridge(实现了SAG)

• sklearn.linear_model.RidgeCV(_BaseRidgeCV, RegressorMixin)

  • 具有l2正则化的线性回归，可以进行交叉验证
  • coef_:回归系数

6.2 改进房价预测案例

# 1.导入数据 load_bostan
data = load_boston()

# 2.数据的基本处理 划分数据集
x_train,x_test,y_train,y_test = train_test_split(data.data,data.target,test_size=0.2,random_state=20)

# 3.特征工程 标准化
# 3.1 初始化标准化转换器
transfer = StandardScaler()
# 3.2 转换数据
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

# 4.机器学习
# 4.1 梯度下降解决
# 构建模型   初始化估计器    设置迭代1000次停止，或者误差值小于0.001停止
estimator = Ridge(alpha=1.0)
# 训练模型
estimator.fit(x_train,y_train)

# 5.模型评估  MSE
# 先求出预测值
y_predict = estimator.predict(x_test)
# 使用MSE 评估
mean_squared_error(y_pred=y_predict,y_true=y_test)

7.模型的加载与保存

• from sklearn.externals import joblib
  • 保存：joblib.dump(estimator, ‘test.pkl’)
  • 加载：estimator = joblib.load(‘test.pkl’)

8.总结