霍夫变换
概述
霍夫变换是一种特征提取,被广泛应用在图像分析、电脑视觉以及数位影像处理。 霍夫变换的基本原理在于利用点与线的对偶性,将原始图像空间的给定的曲线通过曲线表达形式变为参数空间的一个点。这样就把原始图像中给定曲线的检测问题转化为寻找参数空间中的峰值问题。也即把检测整体特性转化为检测局部特性。
霍夫变换于1962年由Paul Hough 首次提出,后于1972年由Richard Duda和Peter Hart推广使用,经典霍夫变换用来检测图像中的直线,后来霍夫变换扩展到任意形状物体的识别,多为圆和椭圆。
霍夫变换在OpenCV中分为霍夫线变换和霍夫圆变换两种,我们下面将分别进行介绍。
霍夫线变换
原理
众所周知, 一条直线在图像二维空间可由两个变量表示. 如:
- 在笛卡尔坐标系: 可由参数: 斜率和截距(m,b) 表示。
- 在极坐标系: 可由参数: 极径和极角(r, θ \theta θ)表示。

对于霍夫变换, 我们将采用第二种方式极坐标系来表示直线. 因此, 直线的表达式可为:
y = ( − c o s θ s i n θ ) x + ( r s i n θ ) y = (-\frac{cos\theta}{sin\theta})x+(\frac{r}{sin\theta}) y=(−sinθcosθ)x+(sinθr)
即
r = x c o s θ + y s i n θ r = xcos\theta+ysin\theta r=xcosθ+ysinθ
-
对于任意一个点 ( x 0 , y 0 ) (x_0,y0) (x0,y0), 我们可以将通过这个点的一族直线统一定义为:
r = x c o s θ + y s i n θ r = xcos\theta+ysin\theta r=xcosθ+ysinθ
表示每一对 ( r θ , θ ) (r_{\theta},\theta) (rθ,θ)代表一条通过点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)的直线 -
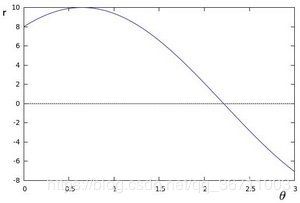
如果对于一个给定点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0),我们在极坐标对极径极角平面绘出所有通过它的直线, 将得到一条正弦曲线. 例如, 对于给定点 x 0 = 8 x_0= 8 x0=8 和 y 0 = 6 y_0= 6 y0=6 我们可以绘出下图 (在平面):
其中 r r r > 0, θ > 2 π \theta > 2\pi θ>2π
-
我们可以对图像中所有的点进行上述操作。如果两个不同点进行上述操作后得到的曲线在平面 θ − r \theta-r θ−r相交, 这就意味着它们通过同一条直线. 例如,使用上面的例子我们继续对点 ( x 1 , y 1 ) (x_1,y_1) (x1,y1)和点 ( x 2 , y 2 ) (x_2,y_2) (x2,y2)绘图, 得到下图:
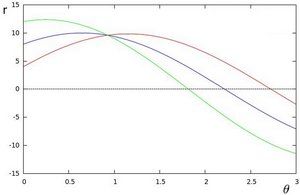
这三条曲线在平面相交于点 (0.925, 9.6), 坐标表示的是参数对 ( θ , r ) (\theta,r) (θ,r)或者是经过点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0) 点 ( x 1 , y 1 ) (x_1,y_1) (x1,y1)和点 ( x 3 , y 3 ) (x_3,y_3) (x3,y3)组成的平面内的的直线。 -
综上所述,一般来说, 一条直线能够通过在平面 ( θ , r ) (\theta,r) (θ,r) 寻找交于一点的曲线数量来检测。而越多曲线交于一点也就意味着这个交点表示的直线由更多的点组成. 。通常,我们可以定义检测一条线所需的最小交叉点数量的阈值。
-
这就是霍夫线变换的作用。它跟踪图像中每个点的曲线之间的交点。如果交叉点的数量大于某个阈值,那么可以认为这个交点所代表的参数对 ( θ , r ) (\theta,r) (θ,r)在原图像中为一条直线。
opencv霍夫变换函数
opencv中主要支持两种霍夫变换:标准霍夫变换和统计概率霍夫变换
标准霍夫变换(HoughLines())
void HoughLines(InputArray image, OutputArray lines, double rho,
double theta, int threshold, double srn=0, double stn=0 )
- 第一个参数,InputArray 类型的 image,输入图像,即源图像,需为8位的单通道二进制图像,可以将任意的源图载入进来后由函数修改成此格式后,再填在这里。
- 第二个参数,InputArray 类型的 lines,经过调用HoughLines函数后储存了霍夫线变换检测到线条的输出矢量。每一条线由具有两个元素的矢量表示 ( ρ , θ ) (\rho,\theta) (ρ,θ),其中, ρ \rho ρ是离坐标原点((0,0)(也就是图像的左上角)的距离。 θ \theta θ是弧度线条旋转角度(0-垂直线,π/2-水平线)。
- 第三个参数,double类型的 ρ \rho ρ,以像素为单位的距离精度。另一种形容方式是直线搜索时的进步尺寸的单位半径。
- 第四个参数,double类型的 theta,以弧度为单位的角度精度。另一种形容方式是直线搜索时的进步尺寸的单位角度。
- 第五个参数,int类型的threshold,累加平面的阈值参数,即识别某部分为图中的一条直线时它在累加平面中必须达到的值。大于阈值threshold的线段才可以被检测通过并返回到结果中。
- 第六个参数,double类型的srn,有默认值0。对于多尺度的霍夫变换,这是第三个参数进步尺寸rho的除数距离。粗略的累加器进步尺寸直接是第三个参数rho,而精确的累加器进步尺寸为rho/srn。
- 第七个参数,double类型的stn,有默认值0,对于多尺度霍夫变换,srn表示第四个参数进步尺寸的单位角度theta的除数距离。且如果srn和stn同时为0,就表示使用经典的霍夫变换。否则,这两个参数应该都为正数。
算法流程
- 读取原始图像,并转换成灰度图,利用阈值分割或者边缘检测算子转换成二值化边缘图像
- 初始化霍夫空间, 令所有 N u m ( θ , ρ ) = 0 Num(\theta,\rho)=0 Num(θ,ρ)=0
- 对于每一个像素点(x,y),在参数空间中找出所有满足
ρ = x c o s θ + y s i n θ \rho = xcos\theta+ysin\theta ρ=xcosθ+ysinθ
的 ( θ , ρ ) (\theta,\rho) (θ,ρ)对,然后令 N u m ( θ , ρ ) = N u m ( θ , ρ ) + 1 Num(\theta,\rho)=Num(\theta,\rho)+1 Num(θ,ρ)=Num(θ,ρ)+1 - 统计所有 N u m ( θ , ρ ) Num(\theta,\rho) Num(θ,ρ)的大小,取出 N u m ( θ , ρ ) > τ Num(\theta,\rho)>\tau Num(θ,ρ)>τ的参数( τ \tau τ是所设的阈值),从而得到一条直线。
- 将上述流程取出的直线,确定与其相关线段的起始点与终止点(有一些算法,如蝴蝶形状宽度,峰值走廊之类)
统计概率霍夫变换(HoughLinesP())
void HoughLinesP(InputArray image, OutputArray lines, double rho, double theta,
int threshold, double minLineLength=0, double maxLineGap=0 )
- 第一个参数,InputArray类型的image,输入图像,即源图像,需为8位的单通道二进制图像,可以将任意的源图载入进来后由函数修改成此格式后,再填在这里。
- 第二个参数,InputArray类型的lines,经过调用HoughLinesP函数后后存储了检测到的线条的输出矢量,每一条线由具有四个元素的矢量(x_1,y_1, x_2, y_2) 表示,其中,(x_1, y_1)和(x_2, y_2) 是是每个检测到的线段的结束点。
- 第三个参数,double类型的rho,以像素为单位的距离精度。另一种形容方式是直线搜索时的进步尺寸的单位半径。
- 第四个参数,double类型的theta,以弧度为单位的角度精度。另一种形容方式是直线搜索时的进步尺寸的单位角度。
[- 第五个参数,int类型的threshold,累加平面的阈值参数,即识别某部分为图中的一条直线时它在累加平面中必须达到的值。大于阈值threshold的线段才可以被检测通过并返回到结果中。 - 第六个参数,double类型的minLineLength,有默认值0,表示最低线段的长度,比这个设定参数短的线段就不能被显现出来。
- 第七个参数,double类型的maxLineGap,有默认值0,允许将同一行点与点之间连接起来的最大的距离。
标准霍夫变换本质上是把图像映射到它的参数空间上,它需要计算所有的M个边缘点,这样它的运算量和所需内存空间都会很大。如果在输入图像中只是处理m(m
算法流程
- 随机抽取图像中的一个特征点,即边缘点,如果该点已经被标定为是某一条直线上的点,则继续在剩下的边缘点中随机抽取一个边缘点,直到所有边缘点都抽取完了为止;
- 对该点进行霍夫变换,并进行累加和计算;
- 选取在霍夫空间内值最大的点,如果该点大于阈值的,则进行步骤4,否则回到步骤1;
- 根据霍夫变换得到的最大值,从该点出发,沿着直线的方向位移,从而找到直线的两个端点;
- 计算直线的长度,如果大于某个阈值,则被认为是好的直线输出,回到步骤1。
源码分析
HoughLines
struct LinePolar
{
float rho;
float angle;
};
struct hough_cmp_gt
{
hough_cmp_gt(const int* _aux) : aux(_aux) {}
inline bool operator()(int l1, int l2) const
{
return aux[l1] > aux[l2] || (aux[l1] == aux[l2] && l1 < l2);
}
const int* aux;
};
static void createTrigTable(int numangle, double min_theta, double theta_step,
float irho, float *tabSin, float *tabCos)
{
float ang = static_cast<float>(min_theta);
for (int n = 0; n < numangle; ang += (float)theta_step, n++)
{
tabSin[n] = (float)(sin((double)ang) * irho);
tabCos[n] = (float)(cos((double)ang) * irho);
}
}
static void findLocalMaximums(int numrho, int numangle, int threshold,
const int *accum, std::vector<int>& sort_buf)
{
for (int r = 0; r < numrho; r++)
for (int n = 0; n < numangle; n++)
{
//得到当前值在累加器数组的位置
int base = (n + 1) * (numrho + 2) + r + 1;
//得到计数值,并以它为基准,看看它是不是局部极大值
if (accum[base] > threshold &&
accum[base] > accum[base - 1] && accum[base] >= accum[base + 1] &&
accum[base] > accum[base - numrho - 2] && accum[base] >= accum[base + numrho + 2])
sort_buf.push_back(base);//把极大值位置存入排序数组内——sort_buf
}
}
static void HoughLinesStandard(const Mat& img, std::vector<Vec2f>& lines, float rho,
float theta,int threshold, int linesMax,double min_theta, double max_theta)
{
int i, j;
float irho = 1 / rho;
//保证输入的图片的正确性
CV_Assert(img.type() == CV_8UC1);
//得到图像的指针
const uchar* image = img.ptr();
int step = (int)img.step; //得到图像的步长
int width = img.cols; //图像的宽
int height = img.rows; //图像的高
if (max_theta < min_theta) {
CV_Error(CV_StsBadArg, "max_theta must be greater than min_theta");
}
//由角和距离的分辨率得到角度和距离的数量,即霍夫变换后角度和距离的个数
int numangle = cvRound((max_theta - min_theta) / theta); //霍夫空间,角度方向的大小
int numrho = cvRound(((width + height) * 2 + 1) / rho); //r的范围,这里以图像的周长作为rho的最大值
//_accum为累加器数组,初始化该霍夫空间
Mat _accum = Mat::zeros((numangle + 2), (numrho + 2), CV_32SC1);
std::vector<int> _sort_buf;
AutoBuffer<float> _tabSin(numangle);
AutoBuffer<float> _tabCos(numangle);
int *accum = _accum.ptr<int>();
float *tabSin = _tabSin, *tabCos = _tabCos;
// 事先计算好sinθi/ρ和cosθi/ρ,查表
createTrigTable(numangle, min_theta, theta,
irho, tabSin, tabCos);
////执行步骤1,逐点进行霍夫空间变换,并把结果放入累加器数组内
for (i = 0; i < height; i++)
for (j = 0; j < width; j++)
{
if (image[i * step + j] != 0)
for (int n = 0; n < numangle; n++)
{
//根据公式: ρ = xcosθ + ysinθ
//cvRound()函数:四舍五入
int r = cvRound(j * tabCos[n] + i * tabSin[n]);
//因为theta是从0到π的,所以cos(theta)是有负的,所以就所有的r += 最大值的一半,让极径都>0
r += (numrho - 1) / 2;
//r表示的是距离,n表示的是角点,在累加器内找到它们所对应的位置(即霍夫空间内的位置),其值加1
accum[(n + 1) * (numrho + 2) + r + 1]++;
}
}
// 执行步骤2,找到局部极大值,即非极大值抑制
// 霍夫空间,局部最大点,采用四邻域判断,比较。(也可以使8邻域或者更大的方式),如果不判断局部最大值,同时选用次大值与最大值,就可能会是两个相邻的直线,但实际是一条直线。
// 选用最大值,也是去除离散的近似计算带来的误差,或合并近似曲线。
findLocalMaximums(numrho, numangle, threshold, accum, _sort_buf);
//执行步骤3,对存储在sort_buf数组内的累加器的数据按由大到小的顺序进行排序
std::sort(_sort_buf.begin(), _sort_buf.end(), hough_cmp_gt(accum));
// stage 4. store the first min(total,linesMax) lines to the output buffer 输出直线
//linesMax是参数,表示最多输出几条直线
linesMax = std::min(linesMax, (int)_sort_buf.size());
//事先定义一个尺度
double scale = 1. / (numrho + 2);
for (i = 0; i < linesMax; i++)
{
//LinePolar 直线的数据结构
//LinePolar结构在该文件的前面被定义
LinePolar line;
//idx为极大值在累加器数组的位置
int idx = _sort_buf[i];
//分离出该极大值在霍夫空间中的位置
//因为n是从0开始的,而之前为了防止越界,所以将所有的n+1了,因此下面要-1,同理r
int n = cvFloor(idx*scale) - 1;
int r = idx - (n + 1)*(numrho + 2) - 1;
line.rho = (r - (numrho - 1)*0.5f) * rho; //因为之前统一将r += (numrho - 1) / 2, 因此需要还原以获得真实的rho
line.angle = static_cast<float>(min_theta) + n * theta;
lines.push_back(Vec2f(line.rho, line.angle)); //用序列存放多条直线
}
}
HoughLinesP
static void HoughLinesProbabilistic(Mat& image, std::vector<Vec4i>& lines, float rho, float theta,
int threshold,int lineLength, int lineGap, int linesMax)
{
Point pt;
float irho = 1 / rho;
RNG rng((uint64)-1); //随机数
CV_Assert(image.type() == CV_8UC1);
int width = image.cols;
int height = image.rows;
int numangle = cvRound(CV_PI / theta);
int numrho = cvRound(((width + height) * 2 + 1) / rho);
//accum为累加器矩阵,霍夫空间,mask为掩码矩阵,大小与输入图像相同
Mat accum = Mat::zeros(numangle, numrho, CV_32SC1);
Mat mask(height, width, CV_8UC1);
//存储事先计算好的正弦余弦值
std::vector<float> trigtab(numangle * 2);
//事先计算好所需的所有正弦和余弦值
for (int n = 0; n < numangle; n++)
{
trigtab[n * 2] = (float)(cos((double)n*theta) * irho);
trigtab[n * 2 + 1] = (float)(sin((double)n*theta) * irho);
}
//复制首地址
const float* ttab = &trigtab[0];
uchar* mdata0 = mask.ptr();
std::vector<Point> nzloc;
// 步骤一:收集图像中的所有非零点,因为输入图像是边缘图像,所以非零点就是边缘点
for (pt.y = 0; pt.y < height; pt.y++)
{
//提取出输入图像和掩码矩阵的每行地址指针
const uchar* data = image.ptr(pt.y);
uchar* mdata = mask.ptr(pt.y);
for (pt.x = 0; pt.x < width; pt.x++)
{
if (data[pt.x])//是非零点
{
mdata[pt.x] = (uchar)1; //掩码相应位置置为1
nzloc.push_back(pt); //将该点加入序列中
}
else
mdata[pt.x] = 0;
}
}
//得到边缘点的数量
int count = (int)nzloc.size();
// 步骤二:随机处理所有的边缘点
for (; count > 0; count--)
{
// 在剩下的边缘点中随机选择一个点,idx为不大于count的随机数
int idx = rng.uniform(0, count);
//max_val为累加器的最大值,max_n为最大值所对应的角度
int max_val = threshold - 1, max_n = 0;
Point point = nzloc[idx];
Point line_end[2]; //定义直线的两个端点
float a, b;
//累加器的地址指针,也就是霍夫空间的地址指针
int* adata = accum.ptr<int>();
int i = point.y, j = point.x, k, x0, y0, dx0, dy0, xflag;
int good_line;
const int shift = 16;
//用序列中的最后一个元素替换被随机提取出来的元素
nzloc[idx] = nzloc[count - 1];
//检测这个坐标点是否已经计算过,也就是它已经属于其他直线
//因为计算过的坐标点会在掩码矩阵mask的相对应位置清零
if (!mdata0[i*width + j])
continue;
// 更新累加器矩阵,找到最有可能的直线
for (int n = 0; n < numangle; n++, adata += numrho)
{
//由角度计算距离
int r = cvRound(j * ttab[n * 2] + i * ttab[n * 2 + 1]);
r += (numrho - 1) / 2;
int val = ++adata[r];
if (max_val < val)
{
max_val = val;
max_n = n;
}
}
// 如果上面得到的最大值小于阈值,则放弃该点,继续下一个点的计算
if (max_val < threshold)
continue;
//从当前点出发,沿着它所在直线的方向前进,直到达到端点为止
a = -ttab[max_n * 2 + 1]; //a=-sinθ
b = ttab[max_n * 2]; //b = cosθ
x0 = j;
y0 = i;
//确定当前点所在直线的角度是在45度~135度之间,还是在0~45或135度~180度之间
//如过是在45度~135度之间
if (fabs(a) > fabs(b))
{
xflag = 1;//置标识位,标识直线的粗略方向
//确定横、纵坐标的位移量
dx0 = a > 0 ? 1 : -1;
dy0 = cvRound(b*(1 << shift) / fabs(a));
y0 = (y0 << shift) + (1 << (shift - 1));
}
//在0~45或135度~180度之间
else
{
xflag = 0; //清标志位
dy0 = b > 0 ? 1 : -1;
dx0 = cvRound(a*(1 << shift) / fabs(b));
x0 = (x0 << shift) + (1 << (shift - 1));
}
//搜索直线的两个端点
for (k = 0; k < 2; k++)
{
//gap表示两条直线的间隙,x和y为搜索位置,dx和dy为位移量
int gap = 0, x = x0, y = y0, dx = dx0, dy = dy0;
//搜索第二个端点的时候,反方向位移
if (k > 0)
dx = -dx, dy = -dy;
//沿着直线的方向位移,直到到达图像的边界或大的间隙为止
for (;; x += dx, y += dy)
{
uchar* mdata;
int i1, j1;
if (xflag)//确定新的位移后的坐标位置
{
j1 = x;
i1 = y >> shift;
}
else
{
j1 = x >> shift;
i1 = y;
}
//如果到达了图像的边界,停止位移,退出循环
if (j1 < 0 || j1 >= width || i1 < 0 || i1 >= height)
break;
//定位位移后掩码矩阵位置
mdata = mdata0 + i1*width + j1;
// for each non-zero point:
// update line end,
// clear the mask element
// reset the gap
//该掩码不为0,说明该点可能是在直线上
if (*mdata)
{
gap = 0;//设置间隙为0
//更新直线的端点位置
line_end[k].y = i1;
line_end[k].x = j1;
}
//掩码为0,说明不是直线,但仍继续位移,直到间隙大于所设置的阈值为止
else if (++gap > lineGap)
break;
}
}
//由检测到的直线的两个端点粗略计算直线的长度
//当直线长度大于所设置的阈值时,good_line为1,否则为0
good_line = std::abs(line_end[1].x - line_end[0].x) >= lineLength ||
std::abs(line_end[1].y - line_end[0].y) >= lineLength;
//再次搜索端点,目的是更新累加器矩阵和更新掩码矩阵,以备下一次循环使用
for (k = 0; k < 2; k++)
{
int x = x0, y = y0, dx = dx0, dy = dy0;
if (k > 0)
dx = -dx, dy = -dy;
// walk along the line using fixed-point arithmetics,
// stop at the image border or in case of too big gap
for (;; x += dx, y += dy)
{
uchar* mdata;
int i1, j1;
if (xflag)
{
j1 = x;
i1 = y >> shift;
}
else
{
j1 = x >> shift;
i1 = y;
}
mdata = mdata0 + i1*width + j1;
// for each non-zero point:
// update line end,
// clear the mask element
// reset the gap
if (*mdata)
{
//if语句的作用是清除那些已经判定是好的直线上的点对应的累加器的值,避免再次利用这些累加值
if (good_line)
{
adata = accum.ptr<int>();
for (int n = 0; n < numangle; n++, adata += numrho)
{
int r = cvRound(j1 * ttab[n * 2] + i1 * ttab[n * 2 + 1]);
r += (numrho - 1) / 2;
adata[r]--;//相应的累加器减1
}
}
//搜索过的位置,不管是好的直线,还是坏的直线,掩码相应位置都清0,这样下次就不会再重复搜索这些位置了,
//从而达到减小计算边缘点的目的
*mdata = 0;
}
//如果已经到达了直线的端点,则退出循环
if (i1 == line_end[k].y && j1 == line_end[k].x)
break;
}
}
//如果是好的直线
if (good_line)
{
Vec4i lr(line_end[0].x, line_end[0].y, line_end[1].x, line_end[1].y);
//把两个端点压入序列中
lines.push_back(lr);
//如果检测到的直线数量大于阈值,则退出该函数
if ((int)lines.size() >= linesMax)
return;
}
}
}
代码结果
opencv调库
int main()
{
Mat dst, cdst, cdstP;
// 载入源图
Mat src = imread("3.jpg", IMREAD_GRAYSCALE);
// 边缘检测
Canny(src, dst, 50, 200, 3);
//转换为灰度图
cvtColor(dst, cdst, COLOR_GRAY2BGR);
cdstP = cdst.clone();
// 标准霍夫变换
vector<Vec2f> lines; //定义一个矢量结构lines用于存放得到的线段矢量集合
HoughLines(dst, lines, 1, CV_PI / 180, 90, 0, 0); // runs the actual detection
// Draw the lines
//HoughLinesStandard(dst, lines, 1, CV_PI / 180, 90, INT_MAX,0,CV_PI);
//依次在图中绘制出每条线段
for (size_t i = 0; i < lines.size(); i++)
{
float rho = lines[i][0], theta = lines[i][1];
Point pt1, pt2;
double a = cos(theta), b = sin(theta);
double x0 = a*rho, y0 = b*rho;
pt1.x = cvRound(x0 + 1000 * (-b));
pt1.y = cvRound(y0 + 1000 * (a));
pt2.x = cvRound(x0 - 1000 * (-b));
pt2.y = cvRound(y0 - 1000 * (a));
line(cdst, pt1, pt2, Scalar(0, 0, 255), 1, CV_AA);
}
// Probabilistic Line Transform
vector<Vec4i> linesP; // will hold the results of the detection
//统计概率霍夫变换
HoughLinesP(dst, linesP, 1, CV_PI / 180, 80, 10, 5); // runs the actual detection
// Draw the lines
//HoughLinesProbabilistic(dst, linesP, 1, CV_PI / 180, 80, 10, 5,INT_MAX);
for (size_t i = 0; i < linesP.size(); i++)
{
Vec4i l = linesP[i];
line(cdstP, Point(l[0], l[1]), Point(l[2], l[3]), Scalar(0, 0, 255), 1, LINE_AA);
}
// Show results
imshow("src_pic", src);
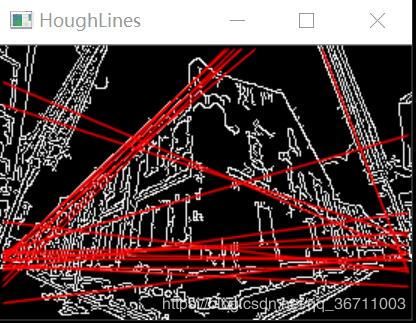
imshow("HoughLines", cdst);
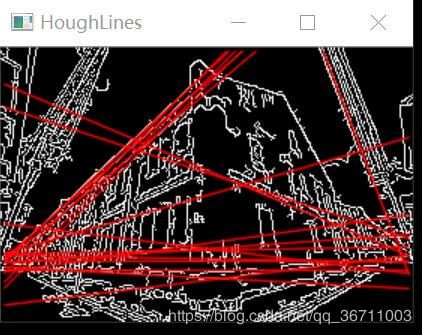
imshow("HoughLinesP", cdstP);
// Wait and Exit
waitKey();
return 0;
}
源代码运行
霍夫圆变换
霍夫圆变换的基本原理和上面讲的霍夫线变化大体上是很类似的,只是点对应的二维极径极角空间被三维的圆心点x, y还有半径r空间取代。说“大体上类似”的原因是,如果完全用相同的方法的话,累加平面会被三维的累加容器所代替:在这三维中,一维是 x,一维是 y,另外一维是圆的半径 r。这就意味着需要大量的内存而且执行效率会很低,速度会很慢。
对直线来说, 一条直线能由参数极径极角 ( r , θ ) (r,\theta) (r,θ)表示. 而对圆来说, 我们需要三个参数来表示一个圆, 也就是: C : ( x c e n t e r , y c e n t e r , r ) C:(x_{center},y_{center},r) C:(xcenter,ycenter,r)
这里的 表示圆心的位置 (下图中的绿点) 而 r 表示半径, 这样我们就能唯一的定义一个圆了, 见下图:

在OpenCV中,我们一般通过一个叫做“霍夫梯度法”的方法来解决圆变换的问题。
霍夫梯度法原理
- 首先对图像应用边缘检测,比如用canny边缘检测。
- 然后,对边缘图像中的每一个非零点,考虑其局部梯度,即用Sobel()函数计算x和y方向的Sobel一阶导数得到梯度。
- 利用得到的梯度,由斜率指定的直线上的每一个点都在累加器中被累加,这里的斜率是从一个指定的最小值到指定的最大值的距离。
- 同时,标记边缘图像中每一个非0像素的位置。
- 然后从二维累加器中这些点中选择候选的中心,这些中心都大于给定阈值并且大于其所有近邻。这些候选的中心按照累加值降序排列,以便于最支持像素的中心首先出现。
- 接下来对每一个中心,考虑所有的非0像素。
- 这些像素按照其与中心的距离排序。从到最大半径的最小距离算起,选择非0像素最支持的一条半径。
- 如果一个中心收到边缘图像非0像素最充分的支持,并且到前期被选择的中心有足够的距离,那么它就会被保留下来。
这个实现可以使算法执行起来更高效,或许更加重要的是,能够帮助解决三维累加器中会产生许多噪声并且使得结果不稳定的稀疏分布问题。
缺陷
- 在霍夫梯度法中,我们使用Sobel导数来计算局部梯度,那么随之而来的假设是,其可以视作等同于一条局部切线,但这个并不是一个数值稳定的做法。在大多数情况下,这样做会得到正确的结果,但或许会在输出中产生一些噪声。
- 在边缘图像中的整个非0像素集被看做每个中心的候选部分。因此,如果把累加器的阈值设置偏低,算法将要消耗比较长的时间。第三,因为每一个中心只选择一个圆,如果有同心圆,就只能选择其中的一个。
- 因为中心是按照其关联的累加器值的升序排列的,并且如果新的中心过于接近之前已经接受的中心的话,就不会被保留下来。且当有许多同心圆或者是近似的同心圆时,霍夫梯度法的倾向是保留最大的一个圆。可以说这是一种比较极端的做法,因为在这里默认Sobel导数会产生噪声,若是对于无穷分辨率的平滑图像而言的话,这才是必须的。
HoughCircles()
void HoughCircles(InputArray image,OutputArray circles, int method,double dp, double minDist, double param1=100,double param2=100, int minRadius=0, int maxRadius=0 )
- 第一个参数,InputArray类型的image,输入图像,即源图像,需为8位的灰度单通道图像。
- 第二个参数,InputArray类型的circles,经过调用HoughCircles函数后此参数存储了检测到的圆的输出矢量,每个矢量由包含了3个元素的浮点矢量(x, y, radius)表示。
- 第三个参数,int类型的method,即使用的检测方法,目前OpenCV中就霍夫梯度法一种可以使用,它的标识符为CV_HOUGH_GRADIENT,在此参数处填这个标识符即可。
- 第四个参数,double类型的dp,用来检测圆心的累加器图像的分辨率于输入图像之比的倒数,且此参数允许创建一个比输入图像分辨率低的累加器。上述文字不好理解的话,来看例子吧。例如,如果dp= 1时,累加器和输入图像具有相同的分辨率。如果dp=2,累加器便有输入图像一半那么大的宽度和高度。
- 第五个参数,double类型的minDist,为霍夫变换检测到的圆的圆心之间的最小距离,即让我们的算法能明显区分的两个不同圆之间的最小距离。这个参数如果太小的话,多个相邻的圆可能被错误地检测成了一个重合的圆。反之,这个参数设置太大的话,某些圆就不能被检测出来了。
- 第六个参数,double类型的param1,有默认值100。它是第三个参数method设置的检测方法的对应的参数。对当前唯一的方法霍夫梯度法CV_HOUGH_GRADIENT,它表示传递给canny边缘检测算子的高阈值,而低阈值为高阈值的一半。
- 第七个参数,double类型的param2,也有默认值100。它是第三个参数method设置的检测方法的对应的参数。对当前唯一的方法霍夫梯度法CV_HOUGH_GRADIENT,它表示在检测阶段圆心的累加器阈值。它越小的话,就可以检测到更多根本不存在的圆,而它越大的话,能通过检测的圆就更加接近完美的圆形了。
- 第八个参数,int类型的minRadius,有默认值0,表示圆半径的最小值。
- 第九个参数,int类型的maxRadius,也有默认值0,表示圆半径的最大值。
源代码解析
static void HoughCirclesGradient(InputArray _image, OutputArray _circles, float dp, float minDist,
int minRadius, int maxRadius, int cannyThreshold,
int accThreshold, int maxCircles, int kernelSize, bool centersOnly)
{
CV_Assert(kernelSize == -1 || kernelSize == 3 || kernelSize == 5 || kernelSize == 7);
//控制dp不能比1小
dp = max(dp, 1.f);
float idp = 1.f / dp;
Mat edges, dx, dy;//edges表示图像边缘矩阵
//Sobel算子,一阶导数边缘检测算子.dx,dy分别表示x和y方向的差分阶数,kernersize核为3,
Sobel(_image, dx, CV_16S, 1, 0, kernelSize, 1, 0, BORDER_REPLICATE);
Sobel(_image, dy, CV_16S, 0, 1, kernelSize, 1, 0, BORDER_REPLICATE);
Canny(dx, dy, edges, std::max(1, cannyThreshold / 2), cannyThreshold, false);
Mutex mtx;//互斥信号量
//设置多线程数
int numThreads = std::max(1, getNumThreads());
//三维霍尔空间
std::vector<Mat> accumVec;
NZPointSet nz(_image.rows(), _image.cols());
//沿着梯度和梯度的反方向,并行计算边缘图像每个像素点
parallel_for_(Range(0, edges.rows),
HoughCirclesAccumInvoker(edges, dx, dy, minRadius, maxRadius, idp, accumVec, nz, mtx),
numThreads);
//计算圆周点的总数
int nzSz = cv::countNonZero(nz.positions);
if (nzSz <= 0)
return;
Mat accum = accumVec[0];
//二维累加器中每个候选中心点
for (size_t i = 1; i < accumVec.size(); i++)
{
accum += accumVec[i];
}
accumVec.clear();
std::vector<int> centers;
// 4 rows when multithreaded because there is a bit overhead
// and on the other side there are some row ranges where centers are concentrated
//并行遍历整个累加器矩阵,找到可能的圆心
parallel_for_(Range(1, accum.rows - 1),
HoughCirclesFindCentersInvoker(accum, centers, accThreshold, mtx),
(numThreads > 1) ? ((accum.rows - 2) / 4) : 1);
//计算圆心的总数
int centerCnt = (int)centers.size();
if (centerCnt == 0)
return;
//对圆心按照由大到小的顺序进行排序
std::sort(centers.begin(), centers.end(), hough_cmp_gt(accum.ptr<int>()));
std::vector<Vec3f> circles;
circles.reserve(256);
if (centersOnly)
{
// 最大半径小于0时,只能得到一个圆心
GetCircleCenters(centers, circles, accum.cols, minDist, dp);
}
else
{
std::vector<EstimatedCircle> circlesEst;
//分两种情况计算圆周半径,一种使用列表法,一种用矩阵法。
if (nzSz < maxRadius * maxRadius)
{
// Faster to use a list
NZPointList nzList(nzSz);
nz.toList(nzList);
// One loop iteration per thread if multithreaded.
//并行计算圆周的半径
parallel_for_(Range(0, centerCnt),
HoughCircleEstimateRadiusInvoker<NZPointList>(nzList, nzSz, centers, circlesEst, accum.cols,
accThreshold, minRadius, maxRadius, dp, mtx),
numThreads);
}
else
{
// 矩阵法,遍历圆周中心,并行计算圆周半径
parallel_for_(Range(0, centerCnt),
HoughCircleEstimateRadiusInvoker<NZPointSet>(nz, nzSz, centers, circlesEst, accum.cols,
accThreshold, minRadius, maxRadius, dp, mtx),
numThreads);
}
// Sort by accumulator value
std::sort(circlesEst.begin(), circlesEst.end(), cmpAccum);
//给定的GetCircle将被连续调用n-1次。结果保存在circles中
std::transform(circlesEst.begin(), circlesEst.end(), std::back_inserter(circles), GetCircle);
//剔除半径小于minRadius的半径圆
RemoveOverlaps(circles, minDist);
}
//返回所有的圆集合
if (circles.size() > 0)
{
int numCircles = std::min(maxCircles, int(circles.size()));
_circles.create(1, numCircles, CV_32FC3);
Mat(1, numCircles, CV_32FC3, &circles[0]).copyTo(_circles.getMat());
return;
}
}
结果展示
int main()
{
// Loads an image
Mat src = imread("1.jpg", IMREAD_COLOR);
Mat gray;
cvtColor(src, gray, COLOR_BGR2GRAY);
medianBlur(gray, gray, 5);
vector<Vec3f> circles;
HoughCircles(gray, circles, HOUGH_GRADIENT, 1, gray.rows / 16, 100, 30, 1, 50);
//HoughCircles1(gray, circles, HOUGH_GRADIENT, 1,gray.rows / 16,100, 30, 1, 50,-1,3);
for (size_t i = 0; i < circles.size(); i++)
{
Vec3i c = circles[i];
Point center = Point(c[0], c[1]);
// circle center
circle(src, center, 1, Scalar(0, 100, 100), 3, LINE_AA);
// circle outline
int radius = c[2];
circle(src, center, radius, Scalar(0, 255, 0), 3, LINE_AA);
}
imshow("detected circles", src);
waitKey();
return 0;
}
参考文章
https://docs.opencv.org/3.4.1/d4/d70/tutorial_hough_circle.html.
https://www.cnblogs.com/kk17/p/9693132.html.
https://docs.opencv.org/3.4.1/d4/d70/tutorial_hough_circle.html.