编译原理习题下(6-9章)
中间代码生成
6.1.1
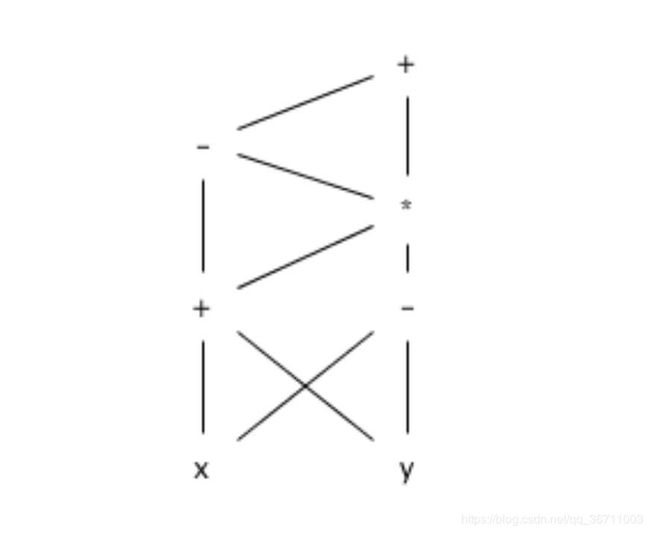
为下面的表达式构造 DAG
( ( x + y ) − ( ( x + y ) ∗ ( x − y ) ) ) + ( ( x + y ) ∗ ( x − y ) ) ((x+y)-((x+y)*(x-y)))+((x+y)*(x-y)) ((x+y)−((x+y)∗(x−y)))+((x+y)∗(x−y))
6.2.2
对下列赋值语句练习下列操作
- a = b[i] + c[j]
- 四元式
| op | arg1 | arg2 | result | |
|---|---|---|---|---|
| 0 | =[] | b | i | t1 |
| 1 | =[] | c | j | t2 |
| 2 | + | t1 | t2 | t3 |
| 3 | = | t3 | a |
- 三元式
| op | arg1 | arg2 | |
|---|---|---|---|
| 0 | =[] | b | i |
| 1 | =[] | c | j |
| 2 | + | (0) | (1) |
| 3 | = | a | 2 |
- 间接三元式
| op | arg1 | arg2 | |
|---|---|---|---|
| 0 | =[] | b | i |
| 1 | =[] | c | j |
| 2 | + | (0) | (1) |
| 3 | = | a | 2 |
| instruction | |
|---|---|
| 0 | (0) |
| 1 | (1) |
| 2 | (2) |
| 3 | (3) |
- a[i] = b*c - b*d
- 四元式
| op | arg1 | arg2 | result | |
|---|---|---|---|---|
| 0 | * | b | c | t1 |
| 1 | * | b | d | t2 |
| 2 | - | t1 | t2 | t3 |
| 3 | []= | a | i | t4 |
| 4 | = | t3 | t4 |
- 三元式
| op | arg1 | arg2 | |
|---|---|---|---|
| 0 | * | b | c |
| 1 | * | b | d |
| 2 | - | (0) | (1) |
| 3 | []= | a | 2 |
| 4 | = | 3 | 2 |
- 间接三元式
| instruction | |
|---|---|
| 0 | (0) |
| 1 | (1) |
| 2 | (2) |
| 3 | (3) |
| 4 | (4) |
- x = f(y+1) + 2
- 四元式
| op | arg1 | arg2 | result | |
|---|---|---|---|---|
| 0 | + | y | 1 | t1 |
| 1 | param | t1 | ||
| 2 | call | f | 1 | t2 |
| 3 | + | t2 | 2 | t3 |
| 4 | = | t3 | x |
- 三元式
| op | arg1 | arg2 | |
|---|---|---|---|
| 0 | + | y | 1 |
| 1 | param | (0) | |
| 2 | call | f | 1 |
| 3 | + | (2) | 2 |
| 4 | = | x | (3) |
- 间接三元式
| op | arg1 | arg2 | |
|---|---|---|---|
| 0 | + | y | 1 |
| 1 | param | (0) | |
| 2 | call | f | 1 |
| 3 | + | (2) | 2 |
| 4 | = | x | (3) |
| instruction | |
|---|---|
| 0 | (0) |
| 1 | (1) |
| 2 | (2) |
| 3 | (3) |
| 4 | (4) |
6.4.3
使用图 6-22 的翻译方案来翻译下列赋值语句:
- x = a[i] + b[j]
三地址码:
t1 = i*awidth
t2 = a[t1]
t3 = j*bwidth
t4 = b[t3]
t5 = t2 + t4
x = t5
- x = a[i][j] + b[i][j]
三地址码:
t1 = i * ai_width
t2 = j * aj_width
t3 = t1 + t2
t4 = a[t3]
t5 = i * bi_width
t6 = j * bj_width
t7 = t5 + t6
t8 = b[t8]
t9 = t4 + t8
x = t9
6.4.8
一个按行存放的实数型数组 A[i, j, k] 的下标 i 的范围为 1~ 4,下标 j 的范围为 0~ 4,且下标 k 的范围为 5~ 10。每个实数占 8 个字节。假设数组 A 从 0 字节开始存放,计算下列元素的位置:
- A[3, 4, 5]
- A[1, 2, 7]
- A[4, 3, 9]
解答
计算公式: ( ( i − 1 ) ∗ 5 ∗ 6 + j ∗ 6 + ( k − 5 ) ) ∗ 8 ((i-1) * 5 * 6 + j * 6 + (k-5)) * 8 ((i−1)∗5∗6+j∗6+(k−5))∗8
- 672
- 112
- 896
6.6.1
在图 6-36 的语法制导定义中添加处理下列控制流构造的规则:
- 一个 repeat 语句:repeat S while B
- !一个 for 循环语句:for (S1; B; S2) S3
| 产生式 | 语义规则 |
|---|---|
| S -> repeat S1 while B | begin = newlabel() S1.next= newlabel() B.true = begin B.false = S.next() S.code = label(begin) || S1.code || label(S1.next) || B.code |
| S -> for (S1; B; S2) S3 | S1.next = newlabel() B.true = newlabel() B.false = S.next S2.next = S1.next S3.next = newlabel() S.code = S1.code || lable(S1.next) || B.code || lable(B.true) || S3.code || label(S3.next) || S2.code || gen(‘goto’, S1.next) |
6.7.1
使用图 6-43 中的翻译方案翻译下列表达式。给出每个子表达式的 truelist 和 falselist。你可以假设第一条被生成的指令的地址是 100.
- a==b && (c == d || e == f)
100: if a == b goto 102
101: goto _
102: if c == d goto _
103: goto 104
104: if e == f goto _
105: goto _
运行时刻环境
7.2.4
7.5.1
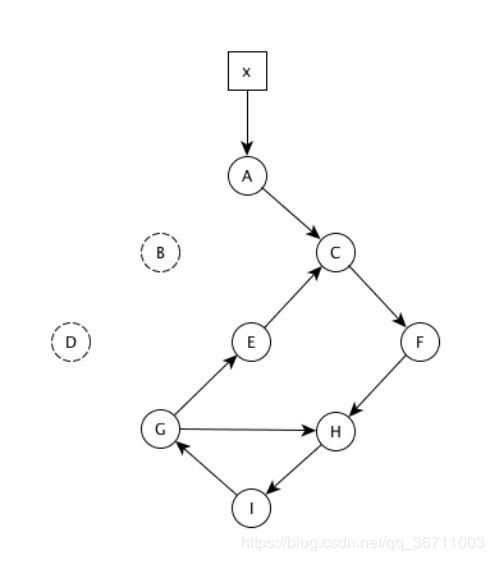
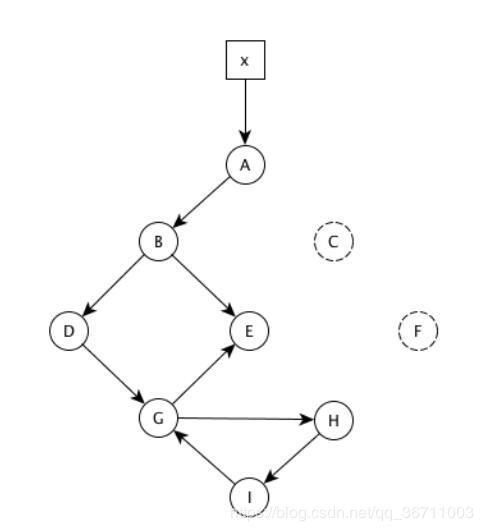
当下列事件发生时,图7-19中的对象的引用计数会发生哪些改变?

- 从A指向B的指针被删除
- 从X指向A的指针被删除
- 结点C被删除
7.6.1
当下列事件发生时,给出标记-清扫式垃圾回收期的处理步骤。
- 图7-19中指针A->B被删除
before: A.reached = … = I.reached = 0
Unscanned = []
line1: A.reached = 1
Unscanned.push(A)
line2~7:
loop1: Unscanned.shift()
C.reached = 1
Unscanned.push( C )
loop2: Unscanned.shift()
F.reached = 1
Uncanned.push(F)
loop3: Unscanned.shift()
H.reached = 1
Uncanned.push(H)
loop4: Unscanned.shift()
I.reached = 1
Uncanned.push(I)
loop5: Unscanned.shift()
G.reached = 1
Uncanned.push(G)
loop6: Unscanned.shift()
E.reached = 1
Uncanned.push(E)
loop7: Unscanned.shift()
// no more object add to list Unscanned
// now it is empty, loop end
line8: Free = []
line9~11: Free = [B, D]
A.reached = C.reached = E.reached = … = I.reached = 0
代码生成
8.2.2
假设a 和b 是元素为4 字节值的数组,为下面的三地址语句序列生成代码
- 四个语句的序列
x = a[i]
y = b[j]
a[i] = y
b[j] = x
- 三个语句的序列
x = a[i]
y = b[i]
z = x*y
- 三个语句的序列
x = a[i]
y = b[x]
a[i] = y
解答
1. LD R1, i
MUL R1, R1, #4
LD R2, a(R1)
LD R3, j
MUL R3, R3, #4
LD R4, b(R3)
ST a(R1), R4
ST b(R3), R2
2. LD R1, i
MUL R1, R1, #4
LD R2, a(R1)
LD R1, b(R1)
MUL R1, R2, R1
ST z, R1
3. LD R1, i
MUL R1, R1, #4
LD R2, a(R1)
MUL R2, R2, #4
LD R2, b(R2)
ST a(R1), R2
8.2.4
假设x、y 和z 存放在内存位置中,为下面的三地址语句序列生成代码
if x < y goto L1
z = 0
goto L2
L1: z = 1
LD R1, x
LD R2, y
SUB R1, R1, R2
BLTZ R1, L1
LD R1, #0
ST z, R1
BR L2
L1: LD R1, #1
ST z, R1
8.5.1
为下面的基本块构造DAG
d = b * c
e = a + b
b = b * c
a = e - d
a[i] = b
b = c + a
d = a[j]
d = c + b
8.6.1
为下面的每个语言赋值语句生成三地址代码
- x = a + b*c;
- a[i] = b[c[i]];
假设其中的所有数组元素都是整数,每个元素占四个字节。(4)中的a、b、c 是常数,它们给出了同名数组的第0 个元素的位置
假设有三个可用的寄存器,适用本节中的简单代码生成算法,把在练习8.6.1‐(1)中的带的三地址代码转换为机器代码。请给出每一个步骤之后的寄存器和地址描述符
三地址代码:
t1 = b*c;
t2 = a+t1;
x = t2;
t1 = i*4;
t2 = c[t1]
t3 = t2*4;
t4 = b[t4];
a[t1] = t4;
机器代码
| R1 | R2 | R3 | x | a | b | c | t1 | t2 | |
|---|---|---|---|---|---|---|---|---|---|
| LD R1,b | b | a | b,R1 | c | |||||
| LD R2,c | b | c | a | b,R1 | c,R2 | ||||
| MUL R1,R1,R2 | t1 | c | a | b | c,R2 | R1 | |||
| LD R3,a | t1 | c | a | a,R3 | b | c,R2 | R1 | ||
| ADD R1,R1,R3 | t2 | c | a | a,R3 | b | c,R2 | R1 | ||
| ST x,R1 | t2 | c | a | R1 | a,R3 | b | c,R2 |
| R1 | R2 | R3 | a[i] | b | c | i | t1 | t2 | t3 | t4 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| LD R1,i | i | a[i] | b | c | i,R1 | ||||||
| MUL R1,R1,4 | t1 | a[i] | b | c | i | R1 | |||||
| LD R2,c(R1) | t1 | t2 | a[i] | b | c | i | R1 | R2 | |||
| MUL R2,R2,4 | t1 | t3 | a[i] | b | c | i | R1 | R2 | |||
| LD R3,b(R2) | t1 | t3 | t4 | a[i] | b | c | i | R1 | R2 | R3 | |
| ST a(R1),R3 | t1 | t3 | t4 | R3 | b | c | i | R1 | R2 |
机器无关优化
9.1.1
对于图9-10中的流图:
- 找出流图中的循环。
- B1中的语句(1)和(2)都是复制语句。其中a和b都被赋予了常量值。我们可以对a和b的哪些使用进行复制传播,并把对它们的使用替换为对一个常量的使用?在所有可能的地方进行这种替换。
- 对每个循环,找出所有的全局公共子表达式。
- 寻找每个循环中的归纳变量。同时要考虑在(2)中引入所有的常量。
- 寻找每个循环的全部循环不变计算。
- B3,B4构成一个循环,B2,B3,B5构成一个循环,入口是B2。
B2:c = 1+b
d = c-1
B4:d = 1+b
B5:b = a+1
e = c-1
t1 = 1+b
t2 = c-1
9.1.4
图9-11中是用来计算两个向量A和B的点积的中间代码。尽你所能,通过下列方式优化这个代码:消除公共子表达式,对归纳变量进行强度消减,消除归纳变量。

dp = 0
i = 0
t1 = i
L: t2 = A[t1]
t4 = B[t1]
t5 = t2*t4
dp = dp+t5
i = i+1
t1 = t1+8
if i < n goto L
9.2.1
对图9-10中的流图,计算下列值:
- 每个基本块的gen和kill集合。
- 每个基本块的IN和OUT集合。
| gen | kill |
|---|---|
| g e n B 1 = { d 1 , d 2 } gen_{B1}=\{d1,d2\} genB1={d1,d2} | k i l l B 1 = { d 8 , d 10 , d 11 } kill_{B1}=\{d8,d10,d11\} killB1={d8,d10,d11} |
| g e n B 2 = { d 3 , d 4 } gen_{B2}=\{d3,d4\} genB2={d3,d4} | k i l l B 2 = { d 5 , d 6 } kill_{B2}=\{d5,d6\} killB2={d5,d6} |
| g e n B 3 = { d 5 } gen_{B3}=\{d5\} genB3={d5} | k i l l B 3 = { d 4 , d 6 } kill_{B3}=\{d4,d6\} killB3={d4,d6} |
| g e n B 4 = { d 6 , d 7 } gen_{B4}=\{d6,d7\} genB4={d6,d7} | k i l l B 4 = { d 4 , d 5 , d 9 } kill_{B4}=\{d4,d5,d9\} killB4={d4,d5,d9} |
| g e n B 5 = { d 8 , d 9 } gen_{B5}=\{d8,d9\} genB5={d8,d9} | k i l l B 5 = { d 2 , d 7 , d 11 } kill_{B5}=\{d2,d7,d11\} killB5={d2,d7,d11} |
| g e n B 6 = { d 10 , d 11 } gen_{B6}=\{d10,d11\} genB6={d10,d11} | k i l l B 6 = { d 1 , d 2 , d 8 } kill_{B6}=\{d1,d2,d8\} killB6={d1,d2,d8} |
I N [ B 2 ] 1 = O U T [ B 1 ] 1 ⋃ O U T [ B 5 ] 0 = 110 0000 0000 + 000 0000 0000 = 110 0000 0000 IN[B_2]^1 = OUT[B_1]^1\bigcup OUT[B_5]^0 = 110\ 0000\ 0000+000\ 0000\ 0000=110\ 0000\ 0000 IN[B2]1=OUT[B1]1⋃OUT[B5]0=110 0000 0000+000 0000 0000=110 0000 0000
O U T [ B 2 ] 1 = g e n B 2 ⋃ ( I N [ B 2 ] 1 − k i l l B 2 ) = 001 1000 0000 + ( 110 0000 0000 − 000 0110 0000 ) = 111 1000 0000 OUT[B_2]^1=gen_{B2}\bigcup (IN[B_2]^1-kill_{B2})=001\ 1000\ 0000+(110\ 0000\ 0000-000\ 0110\ 0000)=111\ 1000\ 0000 OUT[B2]1=genB2⋃(IN[B2]1−killB2)=001 1000 0000+(110 0000 0000−000 0110 0000)=111 1000 0000
| Block B$ | O U T [ B ] 0 OUT[B]^0 OUT[B]0 | I N [ B ] 1 IN[B]^1 IN[B]1 | O U T [ B ] 1 OUT[B]^1 OUT[B]1 | I N [ B ] 2 IN[B]^2 IN[B]2 | O U T [ B ] 2 OUT[B]^2 OUT[B]2 |
|---|---|---|---|---|---|
| B1 | 000 0000 0000 | 000 0000 0000 | 110 0000 0000 | 000 0000 0000 | 110 0000 0000 |
| B2 | 000 0000 0000 | 110 0000 0000 | 111 1000 0000 | 111 0100 1100 | 111 1000 1100 |
| B3 | 000 0000 0000 | 111 1000 0000 | 111 0100 0000 | 111 1011 1100 | 111 0101 1100 |
| B4 | 000 0000 0000 | 111 0100 0000 | 111 0011 0000 | 111 0101 1100 | 111 0011 1000 |
| B5 | 000 0000 0000 | 111 0100 0000 | 101 0100 1100 | 111 0101 1100 | 101 0100 1100 |
| B6 | 000 0000 0000 | 101 0100 1100 | 001 0100 0111 | 101 0100 1100 | 001 0100 0111 |
9.2.3
对图9-10的流图,计算活跃变量分析中的def、use、IN
和OUT集合。
| use | def |
|---|---|
| u s e B 1 = Φ use_{B1}=\Phi useB1=Φ | d e f B 1 = { a , b } def_{B1}=\{a,b\} defB1={a,b} |
| u s e B 2 = { a , b , c } use_{B2}=\{a,b,c\} useB2={a,b,c} | d e f B 2 = { d } def_{B2}=\{d\} defB2={d} |
| u s e B 3 = { b , d } use_{B3}=\{b,d\} useB3={b,d} | d e f B 3 = Φ def_{B3}=\Phi defB3=Φ |
| u s e B 4 = { a , b , e } use_{B4}=\{a,b,e\} useB4={a,b,e} | d e f B 4 = { d } def_{B4}=\{d\} defB4={d} |
| u s e B 5 = { a , b , c } use_{B5}=\{a,b,c\} useB5={a,b,c} | d e f B 5 = { e } def_{B5}=\{e\} defB5={e} |
| u s e B 6 = { a , b , d } use_{B6}=\{a,b,d\} useB6={a,b,d} | d e f B 6 = Φ def_{B6}=\Phi defB6=Φ |
O U T [ B 5 ] 1 = I N [ B 6 ] 1 = { a , b , d } OUT[B_5]^1=IN[B_6]^1=\{a,b,d\} OUT[B5]1=IN[B6]1={a,b,d}
I N [ B 5 ] 1 = u s e B 5 + ( O U T [ B 5 ] 1 − d e f B 5 ) = { a , b , c , d } IN[B_5]^1=use_{B5}+(OUT[B_5]^1-def_{B5})=\{a,b,c,d\} IN[B5]1=useB5+(OUT[B5]1−defB5)={a,b,c,d}
| BlockB | O U T [ B ] 1 OUT[B]^1 OUT[B]1 | I N [ B ] 1 IN[B]^1 IN[B]1 | O U T [ B ] 2 OUT[B]^2 OUT[B]2 | I N [ B ] 2 IN[B]^2 IN[B]2 |
|---|---|---|---|---|
| B6 | a,b,d | a,b,d | ||
| B5 | a,b,d | a,b,c,d | a,b,d | a,b,c,d |
| B4 | a,b,e | a,b,c,d,e | a,b,c,e | |
| B3 | a,b,c,d,e | a,b,c,d,e | a,b,c,d,e | a,b,c,d,e |
| B2 | a,b,c,d,e | a,b,c,e | a,b,c,d,e | a,b,c,e |
| B1 | a,b,c,e | c,e | a,b,c,e | c,e |
这里详细的解答可见:数据流分析详解