Tensorflow2.0之卷积变分自编码器（CVAE）

变分自编码器原理

变分自编码器是一个从隐变量 $Z$ 生成目标数据 $X$ 的模型。更准确地讲，它先假设 $Z$ 服从某些常见的分布（比如正态分布或均匀分布），然后希望训练一个模型 $X=g(Z)$，这个模型能够将原来的概率分布映射到训练集的概率分布，也就是说，其目的是进行分布之间的变换。
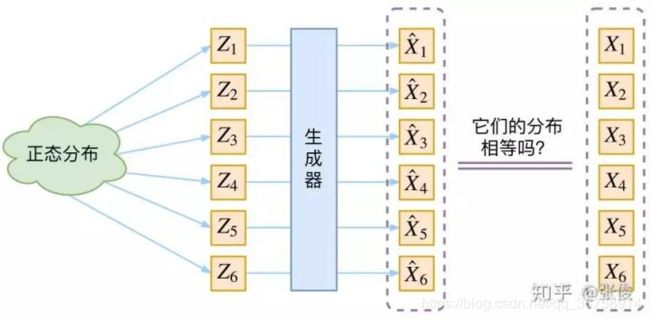接下来，此文章将具体描述 $VAE$ 的构建思路。

第一阶段

首先我们有一批数据样本 $X_1,\dots ,X_N$，其整体用 $X$ 表示，我们可以根据 $X_1,\dots ,X_N$ 得到 $X$ 的分布 $p(X)$，然后直接根据 $p(X)$ 来采样，就可以得到所有可能的 $X$ 了（包括 $X1,\dots ,Xn$ 以外的），这样一来，生成模型就实现了。
但在实际上我们是得不到 $X$ 的分布的，于是我们将 $p(X)$ 重新定义为：
$$p(X)=\sum _{Z}p(X|Z)p(Z)$$

在上式中，$p(X|Z)$ 是由 $Z$ 生成 $X$ 的模型，假设 $Z$ 服从标准正态分布，也就是 $p(Z)=N(0,1)$，那么我们就可以先从标准正态分布中采样一个 $Z$，然后根据 $Z$ 来算一个 $X$，也可以达到生成目的。此时 $VAE$ 的示意图为：

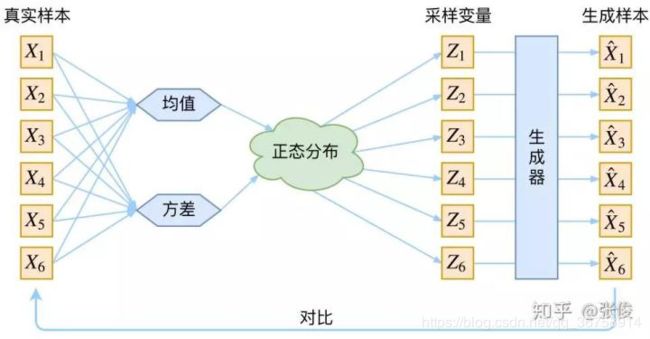
但是我们其实完全不清楚，究竟经过重新采样出来的 $Z_k$，是不是还对应着原来的 $X_k$，所以我们如果直接最小化 $D({\hat{X}}_k,X_k{)}^2$（这里 $D$ 代表某种距离函数）是很不科学的。

第二阶段

其实，在整个 $VAE$ 模型中，我们并没有去使用 $p(Z)$（先验分布）是正态分布的这个假设，而是假设 $p(Z|X)$（后验分布）是正态分布。
具体来说，给定一个真实样本 $X_k$，我们假设存在一个专属于 $X_k$ 的分布 $p(Z|X_k)$（学名叫后验分布），并进一步假设这个分布是（独立的、多元的）正态分布。
所以现在 $p(Z|X_k)$ 专属于 $X_k$，我们有理由说从这个分布采样出来的 $Z$ 应该要还原到 $X_k$ 中去。
接下来，我们需要找出专属于样本 $X_k$ 的正态分布 $p(Z|X_k)$ 的均值 $\mu$ 和方差 ${\sigma }^2$。
于是我们构建两个神经网络 ${\mu }_k=f_1(X_k)$，$log({\sigma }_k^2)=f_2(X_k)$ 来算它们。之所以选择拟合 $log({\sigma }_k^2)$ 而不是直接拟合 ${\sigma }_k^2$，是因为 ${\sigma }_k^2$ 总是非负的，需要加激活函数处理，而拟合 $log({\sigma }_k^2)$ 不需要加激活函数，因为它可正可负。
得到 ${\mu }_k$ 和 ${\sigma }_k^2$ 之后，$p(Z|X_k)$ 的正态分布就已经确定了，此时从其中采样一个 $Z_k$ 出来，然后经过一个生成器得到 ${\hat{X}}_k=g(Z_k)$。这之后，我们可以放心地最小化 $D({\hat{X}}_k,X_k{)}^2$ 了，因为 $Z_k$ 是从专属 $X_k$ 的分布中采样出来的，这个生成器应该要把开始的 $X_k$ 还原回来。于是此时 $VAE$ 的示意图为：
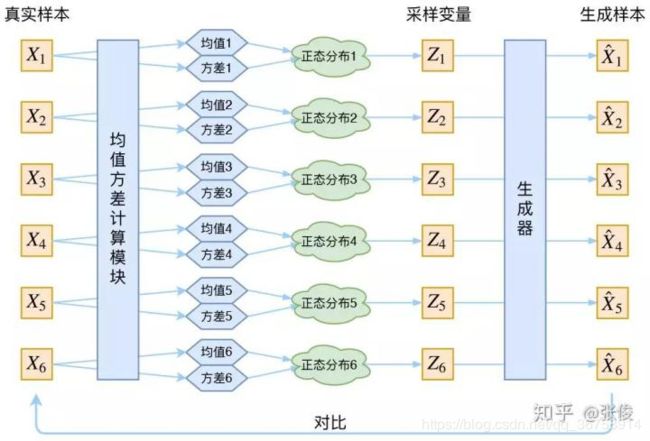事实上，$VAE$ 是为每个样本构造专属的正态分布，然后采样来重构。

第三阶段

首先，我们希望重构 $X$，也就是最小化 $D({\hat{X}}_k,X_k{)}^2$，但是这个重构过程受到噪声的影响，因为 $Z_k$ 是通过重新采样得到的，而不是直接由 $Encoder$ 算出来的。
显然噪声会增加重构的难度，不过好在这个噪声强度（也就是方差）是通过一个神经网络算出来的，所以最终模型为了重构得更好，肯定会想尽办法让方差为0。
而方差为0的话，也就没有随机性了，所以不管怎么采样其实都只是得到确定的结果（也就是均值），只拟合一个当然比拟合多个要容易，而均值是通过另外一个神经网络算出来的。
也就是说，模型会慢慢退化成普通的 $AutoEncoder$，噪声不再起作用。
为了防止了噪声为零，同时保证模型具有生成能力，$VAE$ 还让所有的 $p(Z|X)$ 都向标准正态分布看齐。
也就是说，如果所有的 $p(Z|X)$ 都很接近标准正态分布 $N(0,1)$，那么根据定义：
$$p(Z)=\sum _{X}p(Z|X)p(X)=\sum _{X}N(0,1)p(X)=N(0,1)\sum _{X}p(X)=N(0,1)$$

这样我们就能达到我们的先验假设：$p(Z)$ 是标准正态分布。然后我们就可以放心地从 $N(0,1)$ 中采样来生成图像了。即：

那么，如何让所有的 $p(Z|X)$ 都向 $N(0,1)$ 看齐呢？此时，我们使用一般（各分量独立的）正态分布与标准正态分布的 $KL$ 散度 $KL(N(\mu ,{\sigma }^2)||N(0,1))$ 作为额外的 $loss$，计算结果为：
$$L_{\mu ,{\sigma }^2}=\frac{1}{2}\sum _{i=1}^d({\mu }_{(i)}^2+{\sigma }_{(i)}^2-log({\sigma }_{(i)}^2)-1)$$
上式中的 $d$ 是隐变量 $Z$ 的维度，而 ${\mu }_{(i)}$ 和 ${\sigma }_{(i)}^2$分别代表一般正态分布的均值向量和方差向量的第 $i$ 个分量。
上式的推导过程：
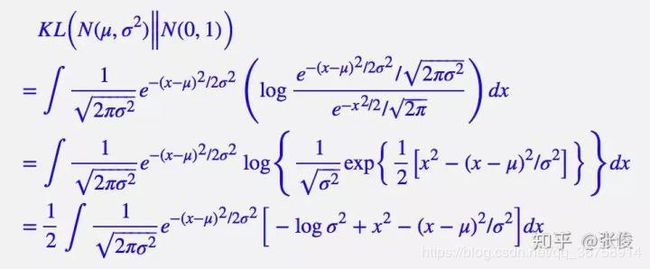整个结果分为三项积分，第一项实际上就是 $-log({\sigma }^2)$ 乘以概率密度的积分（也就是 1），所以结果是 $-log({\sigma }^2)$；第二项实际是正态分布的二阶矩，为 ${\mu }^2+{\sigma }^2$；而根据定义，第三项实际上就是“减均值除以方差=1”。所以总结果就是：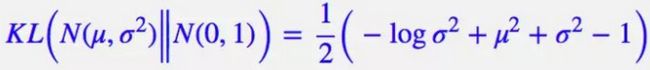

第四阶段（重参数技巧）

其实很简单，就是我们要从 $p(Z|X_k)$ 中采样一个 $Z_k$ 出来，尽管我们知道了 $p(Z|X_k)$ 是正态分布，但是均值方差都是靠模型算出来的，我们要靠这个过程反过来优化均值方差的模型，但是“采样”这个操作是不可导的，而采样的结果是可导的，于是我们利用一个事实：从 $N(\mu ,{\sigma }^2)$ 中采样一个 $Z$，相当于从 $N(0,1)$ 中采样一个 $ϵ$，然后让 $Z=\mu +ϵ\times \sigma$。即：

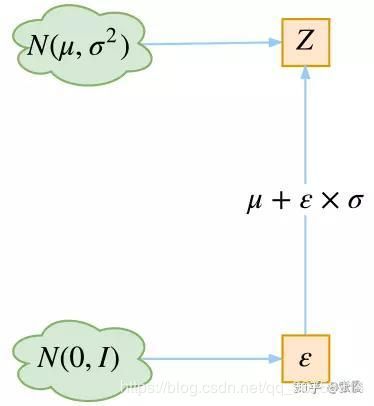
所以，我们将从 $N(\mu ,{\sigma }^2)$ 采样变成了从 $N(0,1)$ 中采样，然后通过参数变换得到从$N(\mu ,{\sigma }^2)$ 中采样的结果。这样一来，“采样”这个操作就不用参与梯度下降了，改为采样的结果参与，使得整个模型可训练了。

VAE的本质

$VAE$ 虽然也是 $AutoEncoder$ 的一种，但它的原理有所不同。
在 $VAE$ 中，它的 $Encoder$ 有两个，一个用来计算均值，一个用来计算方差，这是别具一格的。
它本质上就是在我们常规的自编码器的基础上，对 $Encoder$ 的结果（在 $VAE$ 中对应着计算均值的网络）加上了“高斯噪声”，使得结果 $Decoder$ 能够对噪声有鲁棒性；而那个额外的 $KLloss$（目的是让均值为 0，方差为 1），事实上就是相当于对 $Encoder$ 的一个正则项，希望 $Encoder$ 出来的东西均有零均值。
那另外一个 $Encoder$（对应着计算方差的网络）用来动态调节噪声的强度的。
直觉上来想，当 $Decoder$还没有训练好时（重构误差远大于 $KLloss$），就会适当降低噪声（$KLloss$ 增加），使得拟合起来容易一些（重构误差开始下降）。
反之，如果 $Decoder$ 训练得还不错时（重构误差小于 $KLloss$），这时候噪声就会增加（$KLloss$ 减少），使得拟合更加困难了（重构误差又开始增加），这时候 $Decoder$ 就要想办法提高它的生成能力了。

代码实现

1、导入需要的库

import tensorflow as tf

import numpy as np
import matplotlib.pyplot as plt

from IPython import display

2、导入数据集

(train_images, _), (test_images, _) = tf.keras.datasets.mnist.load_data()

3、图像处理

增加维度

train_images = train_images.reshape(train_images.shape[0], 28, 28, 1).astype('float32')
test_images = test_images.reshape(test_images.shape[0], 28, 28, 1).astype('float32')

标准化

# 标准化图片到区间 [0., 1.] 内
train_images /= 255.
test_images /= 255.

二值化

# 二值化
train_images[train_images >= .5] = 1.
train_images[train_images < .5] = 0.
test_images[test_images >= .5] = 1.
test_images[test_images < .5] = 0.

使用 tf.data 来将数据分批和打乱

TRAIN_BUF = 60000
BATCH_SIZE = 100
TEST_BUF = 10000

train_dataset = tf.data.Dataset.from_tensor_slices(train_images).shuffle(TRAIN_BUF).batch(BATCH_SIZE)
test_dataset = tf.data.Dataset.from_tensor_slices(test_images).shuffle(TEST_BUF).batch(BATCH_SIZE)

4、建立CVAE模型

class CVAE(tf.keras.Model):
    def __init__(self, latent_dim):
        super(CVAE, self).__init__()
        self.latent_dim = latent_dim
        self.inference_net = tf.keras.Sequential(
          [
              tf.keras.layers.InputLayer(input_shape=(28, 28, 1)),
              tf.keras.layers.Conv2D(
                  filters=32, kernel_size=3, strides=(2, 2), activation='relu'),
              tf.keras.layers.Conv2D(
                  filters=64, kernel_size=3, strides=(2, 2), activation='relu'),
              tf.keras.layers.Flatten(),
              # No activation
              tf.keras.layers.Dense(latent_dim + latent_dim),
          ]
        )

        self.generative_net = tf.keras.Sequential(
            [
              tf.keras.layers.InputLayer(input_shape=(latent_dim,)),
              tf.keras.layers.Dense(units=7*7*32, activation=tf.nn.relu),
              tf.keras.layers.Reshape(target_shape=(7, 7, 32)),
              tf.keras.layers.Conv2DTranspose(
                  filters=64,
                  kernel_size=3,
                  strides=(2, 2),
                  padding="SAME",
                  activation='relu'),
              tf.keras.layers.Conv2DTranspose(
                  filters=32,
                  kernel_size=3,
                  strides=(2, 2),
                  padding="SAME",
                  activation='relu'),
              # No activation
              tf.keras.layers.Conv2DTranspose(
                  filters=1, kernel_size=3, strides=(1, 1), padding="SAME"),
            ]
        )

    def sample(self, eps=None):
        if eps is None:
            eps = tf.random.normal(shape=(100, self.latent_dim))
        return self.decode(eps, apply_sigmoid=True)

    def encode(self, x):
        mean, logvar = tf.split(self.inference_net(x), num_or_size_splits=2, axis=1)
        return mean, logvar

    def reparameterize(self, mean, logvar):
        eps = tf.random.normal(shape=mean.shape)
        return eps * tf.exp(logvar * .5) + mean

    def decode(self, z, apply_sigmoid=False):
        logits = self.generative_net(z)
        if apply_sigmoid:
            probs = tf.sigmoid(logits)
            return probs

        return logits

其中，

• latent_dim 是指要用多少个噪声点生成一张图像。
• 在 tf.keras.layers.Dense(latent_dim + latent_dim) 中，输出的维度之所以为两个 latent_dim，是因为我们希望 inference_net 的输出是均值和方差（的对数），所以 inference_net （也就是 Encoder）可以被看成两个神经网络。
• sample() 函数用于将噪声输入 $Decoder$，即 $\hat{X}=g(Z)$ 的过程。
• encode() 函数是编码过程，有两个输出，分别对应 ${\mu }_k=f_1(X_k)$ 和 $log({\sigma }_k^2)=f_2(X_k)$。其中，${\mu }_k$ 和 $log({\sigma }_k^2)$ 都是 latent_dim 维的向量。
• reparameterize() 函数对应着重采样过程，即 $Z=\mu +ϵ\times \sigma$，其中 $ϵ$ 是从 $N(0,1)$ 中采样出来的，经过从 $ϵ$ 到 $Z$ 的变换后得到的结果，与直接从 $N(\mu ,{\sigma }^2)$ 中采样一个 $Z$ 一致。
• decode() 函数即 sample() 函数的具体实现过程。

5、初始化优化器

optimizer = tf.keras.optimizers.Adam(1e-4)

6、定义损失函数

定义正态分布概率密度的对数

正态分布的概率密度为：

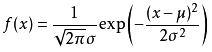
所以其对数为：
$$-\frac{1}{2}[\frac{(x-\mu {)}^2}{{\sigma }^2}+ln(2\pi {\sigma }^2)]$$

def log_normal_pdf(sample, mean, logvar, raxis=1):
    # 正态分布概率密度的对数
    log2pi = tf.math.log(2. * np.pi)
    return tf.reduce_sum(
        -.5 * ((sample - mean) ** 2. * tf.exp(-logvar) + logvar + log2pi),
        axis=raxis)

计算损失

经过第一部分的原理分析，在变分自编码器中，其损失除了常规的交叉熵损失之外，还有关于 $KL$ 散度的损失。

def compute_loss(model, x):
    mean, logvar = model.encode(x)
    z = model.reparameterize(mean, logvar)
    x_logit = model.decode(z)

    cross_ent = tf.reduce_sum(tf.nn.sigmoid_cross_entropy_with_logits(logits=x_logit, labels=x), axis=[1, 2, 3])
    KLD = -0.5 * tf.reduce_sum(1 + logvar- tf.pow(mean, 2) - tf.exp(logvar), axis=-1)
    return tf.reduce_mean(cross_ent + KLD)

对以上代码中的变量进行分析

取一批训练集样本

for x in train_dataset.take(1):
    print(x.shape)

(100, 28, 28, 1)

即一批样本包含100个样本。

将样本输入编码器

model = CVAE(latent_dim)
mean, logvar = model.encode(x)
print(mean.shape)
print(logvar.shape)

(100, 50)
(100, 50)

即每个样本对应的正态分布的均值和方差（的对数）都是50维向量。

重参数过程

z = model.reparameterize(mean, logvar)
print(z.shape)

(100, 50)

因为重参数过程中有 $Z=\mu +ϵ\times \sigma$，所以每个采样样本 $Z$ 的维度是和噪声维度相同的，即50维。

将 Z 输入解码器

x_logit = model.decode(z)
print(x_logit.shape)

(100, 28, 28, 1)

即最终得到的形状和最早输入的形状一致。

交叉熵损失

cross_ent = tf.reduce_sum(tf.nn.sigmoid_cross_entropy_with_logits(logits=x_logit, labels=x), axis=[1, 2, 3])
print(cross_ent.shape)

(100,)

其中的 axis=[1, 2, 3] 表示这个操作是在后三个维度上进行（因为 x 和 x_logit 都是四维的），即最终结果的形状将只剩下第一维度（即 $[100,28,28,1]\to [100,]$）。

KL散度损失

KLD = -0.5 * tf.reduce_sum(1 + logvar- tf.pow(mean, 2) - tf.exp(logvar), axis=-1)
print(KLD.shape)

(100,)

其中的 axis=-1 表示这个操作是在最后一个维度上进行（ mean 和 logvar 都是二维的），即最终结果的形状将只剩下第一维度（即 $[100,50]\to [100,]$）。

7、定义梯度下降函数

def compute_apply_gradients(model, x, optimizer):
    with tf.GradientTape() as tape:
        loss = compute_loss(model, x)
    gradients = tape.gradient(loss, model.trainable_variables)
    optimizer.apply_gradients(zip(gradients, model.trainable_variables))

8、定义显示图像函数

def generate_and_save_images(model, epoch, test_input):
    predictions = model.sample(test_input)
    fig = plt.figure(figsize=(4,4))

    for i in range(predictions.shape[0]):
        plt.subplot(4, 4, i+1)
        plt.imshow(predictions[i, :, :, 0], cmap='gray')
        plt.axis('off')

    # tight_layout 最小化两个子图之间的重叠
    plt.savefig('image_at_epoch_{:04d}.png'.format(epoch))
    plt.show()

9、训练模型

epochs = 100
latent_dim = 50
num_examples_to_generate = 16

# 保持随机向量恒定以进行生成（预测），以便更易于看到改进。
random_vector_for_generation = tf.random.normal(
    shape=[num_examples_to_generate, latent_dim])
model = CVAE(latent_dim)

generate_and_save_images(model, 0, random_vector_for_generation)

for epoch in range(1, epochs + 1):
    for train_x in train_dataset:
        compute_apply_gradients(model, train_x, optimizer)

    if epoch % 1 == 0:
        loss = tf.keras.metrics.Mean()
        for test_x in test_dataset:
            loss(compute_loss(model, test_x))
        elbo = loss.result()
        display.clear_output(wait=False)
        print('Epoch: {}, Test set ELBO: {}, '.format(epoch,
                                                        elbo))
    generate_and_save_images(
        model, epoch, random_vector_for_generation)

参考资料

变分自编码器VAE：原来是这么一回事 | 附开源代码