同济高数上第七版习题1.1精解
1.求下列函数的自然定义域。
(1)
解:根号下需大于等于0,故,所以,即定义域为)。
(2)
解:分母不能为0,所以。
(3)
解:由题意得,且,所以定义域为。
(4)
解:,所以定义域为。
(5)
解:因为正弦函数的定义域为,所以只需。
(6)
解:因为正切函数的定义域中不可以包含,所以,。
(7)
解:因为,所以。
(8)
解:此时需要同时满足,所以定义域为。
(9)
解:由对数函数定义域可知,所以。
(10)
解:。
2.下列各题中,函数和是否相同?为什么?
(1),.
解:不同。因为定义域不同,定义域不可以等于0,
定义域需要大于0。
(2) ,
解:不同。因为对应法则不同,只能输出正数。此题不要说因为值域不同,因为就算值域相同也未必是函数相同。
(3) ,
解:此题在三次根号下,直接提出了,无需讨论。故相同。
(4) ,
解:不同。因为定义域不同。
3.
计算,,,。
解:计算时用到上面的式子得到,,,。图形略。
4.试证下列函数在指定区间内的单调性。
(1) ,。
解:题外话,在不久的将来,单调性会用导数知识来讨论。
在定义域内任取,并设。则,所以单调增加。
(2),。
解:同样的话说两次。在定义域内任取,并设。则,所以单调增加。
5.设为定义在内的奇函数,若在内单调增加,证明在内也单调增加
证明:在内任取,并设,因为在内单调增加,所以。取负号,则,此时二者属于。那么,说明在内,函数值依然随着自变量增加而递增。故单调增加。
6.下面的函数都是定义在区间上的,证明:
(1)两个偶函数的和是偶函数,两个奇函数的和是奇函数;
(2)两个偶函数的乘积是偶函数,两个奇函数的乘积也是偶函数,偶函数与奇函数的成绩是奇函数。
证明:(1)设函数为偶函数,二者的和函数,则。即两个偶函数的和是偶函数。
同样,设函数为奇函数,二者的和函数,则。即两个奇函数的和是奇函数。
(2)设函数为偶函数,二者的乘积为,则。即两个偶函数的乘积是偶函数。
同样,设函数为奇函数,二者的乘积为,则。即两个奇函数的乘积是偶函数。
设函数为偶函数,为奇函数,二者的乘积为,则。即结果为奇函数。
7.下列函数中哪些是偶函数,哪些是奇函数,哪些是非奇非偶函数?
题外话:判断奇偶性时,可以大致先判断一下定义域,如果定义域不是关于原点对称。则直接得出结论。
(1)
解:,所以为偶函数。
(2)
解:,哪个都靠不上,所以为非奇非偶函数。
(3)
解:,所以为偶函数。
(4)
解:,所以为奇函数。
(5)
解:,哪个都靠不上,所以为非奇非偶函数。
(6)
解:,所以为偶函数。
8.下列函数哪些是周期函数?对于周期函数,指出其周期。
(1)
解:是周期函数,周期为。
(2)
解:是周期函数。周期为。
(3)
解:是周期函数。周期为。
(4)
解:不是周期函数。
(5)
解:是周期函数。因为。所以周期为。
9.求下列函数的反函数。
(1)
解:因为,所以。
(2)
解:,所以可以解得。
(3)
解:,所以,其中这个条件说明函数不是常数函数。
(4)
解:因为,。
(5)
解:,所以。
(6)
解:,所以,得到。
10.设函数在数集上有定义,试证:函数在X上有界的充分必要条件是它在上既有上界又有下界。
证明:先证必要性。如果函数在上有界,则说明存在一个正数,使得对于任意的 ,有,即,则既有上界又有下界。
充分性。不妨设函数在数集上的上界为,下界为。取。在数集上一定有。所以函数有界。
11.在下列各题中,求由所给函数构成的复合函数,并求这函数分别对应于给定自变量和的函数值:
(1)
解:,,。
(2)
解:,,.
(3)
解:,,
(4)
解:,,。
(5)
解:
12.设的定义域,求下列函数的定义域。
(1)
解:,所以。
(2)
解:,所以。
(3)
解:,所以。
(4)
解: 同时,所以并且,所以,当时,即有公共部分,当时,无公共部分。
13.设,。求和。
解:
14.一直水渠的横断面为等腰梯形,斜角。当过水断面的面积为定值时。求四周与水深之间的函数关系式,并指出其定义域。
解:根据梯形面积公式有,整理得到,同时横断面为等腰梯形,需要最下方的边长可得。
15.设平面上有正方形及直线。若表示正方形位于直线左下方部分的面积,试求与之间的函数关系。
解:请自行画个图。
由图不难看出,当时,面积是.
当时,有两种方法,第一种是用一个和两个坐标轴所围的等腰直角三角形减去左上和右下两个一样大小的小等腰三角形面积。大等腰直角三角形面积是。两个小等腰直角三角形面积之和为2倍的。二者相减后得到。此情况下还有一种解法就是用整个正方形面积1减去被所截出来的五边形面积(不再赘述)。
当时面积为1。
16.求华氏温度()和摄氏温度()二者之间的转换公式。并求:
(1)的等价摄氏温度和的等价华氏温度。
(2)是否存在一个温度值,使得华氏温度计数和摄氏温度计数是一样的?如果存在,那么温度值是多少?
解:华氏温度和摄氏温度二者为线性关系,设关系式为,为常数。当相当于,相当于,代入后可求得.
由此可以求得(1)的等价摄氏温度,的等价华氏温度为。
(2)假设存在哪个温度,并设为。则会有,所以可求出。
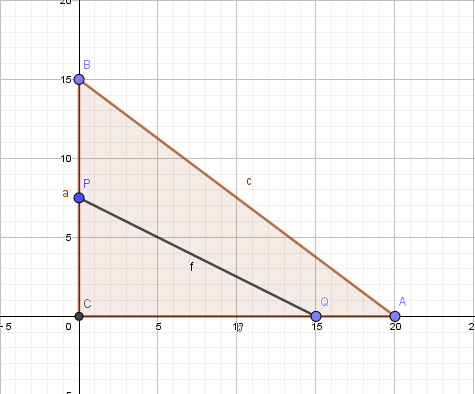
17.已知直角三角形中,直角边的长度分别为20,15.动点从出发,沿三角形边界按方向移动;动点从出发,沿三角形边界按方向移动,移动到两动点相遇时为止,且点移动的速度是点移动的速度的2倍。设动点移动的距离为,三角形的面积为,试求与之间的函数关系。
解:由题意可知。三角形另一边长为25,并且经过计算可知在当时,动点会在在斜边上相遇。
(1)
直接计算可得。此时。
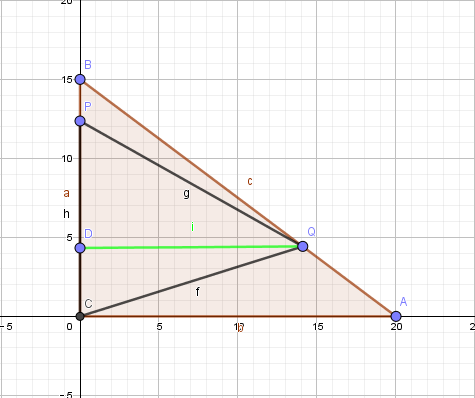
(2)
当s时,过点向做垂足D.根据比例关系可得,可以得出:。可得,所以。
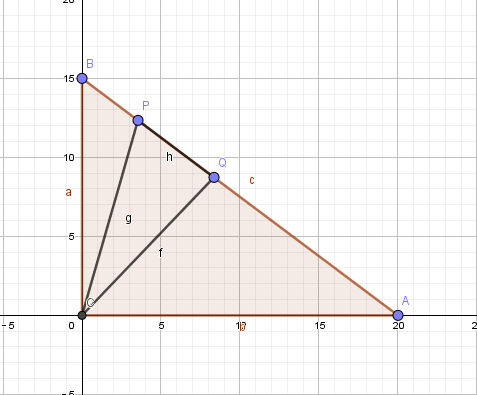
(3)
此时,在直角三角形中,易得到到斜边的距离为。有根据题意得,长度为,长度为,故长度为。所以面积。
终上所述
18.利用以下美国人口普查局提供的世界人口数据以及指数模型来推 测 2020 年的世界人口。
解:此题属于数学建模类题目,在此讲解较为简单的一种方法。
利用第三列数据,将其平均得到年平均增长率约为1.1282%,为便于计算,约等于0.011。然后以2008年为基期。年后的人口数量方程为,2020年时对应的代入后约等于70亿。受资源,环境等因素的影响,人口数量不能无限制增加。所以该模型对长期人口预测结果偏差较大。