论文笔记 Neural Graph Collaborative Filtering [SIGIR 2019 ]
[SIGIR 2019 ] Neural Graph Collaborative Filtering
paper | codes | author
摘要
学习用户和商品的表示是现代推荐系统的核心。从早期的矩阵分解,到最近的深度学习,现有的工作都是从用户和上项目的现有特性(比如ID、属性),映射得到它们的嵌入表示。这往往忽略两者之间的collaborative signal,因此,产生的嵌入不能很好地捕获协作过滤效果。
模型介绍
如图所示,模型分三层:
1. Embedding Layer 嵌入层:与其他主流推荐模型类似,本文用维度为d的嵌入向量来描述用户、项目。
2. Embedding Propagation Layers:传播层,通过提取high-order connectivity来细化嵌入。
3.Prediction Layer:预测。
Embedding Propagation Layers
传统推荐模型中,会将嵌入直接作为用户、项目表示,得到最终的推荐评分,但是本文中,用户项目的嵌入,仅仅作为Embedding Propagation Layers的初始输入。
作者从单层的嵌入传播开始介绍。
1 First-order Propagation
使用一个项目的用户可以被视为该项目的特性,并用于度量两个项目之间的协作相似性。因此,在一阶信息传播中,分为两步:信息构建、信息聚合。
1.1 Message Construction
其中,![]() 是编码函数,它的输入是用户和项目的嵌入
是编码函数,它的输入是用户和项目的嵌入![]() ,
,![]() 就是边(u,i)的衰减因子,意义在于信息会随着路径传播而衰减。
就是边(u,i)的衰减因子,意义在于信息会随着路径传播而衰减。
具体公式如下:
![]() 是可训练的权重矩阵,维度为d×d。
是可训练的权重矩阵,维度为d×d。
![]() 是用户u和项目i的第一跳邻居,在此处,设
是用户u和项目i的第一跳邻居,在此处,设 ![]() (graph Laplacian norm)。
(graph Laplacian norm)。
1.2 Message Aggregation
一阶信息传播后,要将一个用户的所有一跳项目的信息都聚合到一起,同时还要考虑它自身的表示。因此,用户u的嵌入可以被定义为
LeakyReLU允许消息对正信号和小的负信号进行编码。
2 High-order Propagation
上述一阶连通性可以增强表示,作者可以叠加更多的嵌入传播层来探索高阶连通性信息。这种高阶连接度是对协作信号进行编码以估计用户与项目之间的相关分数的关键。对于多层传播,信息传播公式可以定义为:
其中,![]() 是共享的权值矩阵。
是共享的权值矩阵。
同样地,用户u的嵌入可以定义为:
3 矩阵表示
为了提供嵌入传播的整体视图并方便批量实现,作者提供了分层传播规则的矩阵形式,与多层传播的两个公式等价。
其中,![]() 是所有用户和项目的表示。
是所有用户和项目的表示。
![]() 是拉普拉斯矩阵,R是用户和项目的交互矩阵,D是对角矩阵。其中,
是拉普拉斯矩阵,R是用户和项目的交互矩阵,D是对角矩阵。其中,![]() ,因此,
,因此,![]() 等价于衰减因子
等价于衰减因子![]() 。
。
(此处的数学关系还要巴拉巴拉)
Prediction Layer
在最后,会得到多个用户表示{ ![]() }。
}。
由于在不同层中获得的表示强调通过不同连接传递的消息,因此它们在反映用户偏好方面有不同的贡献。因此,作者将它们串联起来,构成一个用户的最终嵌入。
项目的表示,也做类似的处理。
为何使用串联:除了串联,其他聚合器也可以应用,比如:加权平均、最大池、LSTM。应用不同的结合方式,意味着不同的效果。
使用串联的优点在于它的简单性,因为它不需要额外的参数来学习,而且在最近的图神经网络的工作中已经非常有效地证明了这一点,这涉及到分层聚合机制。
用内积来评估:
其他补充
损失函数
Message and Node Dropout
深度学习模型虽然具有较强的表示能力,但往往存在过拟合问题。Dropout是防止神经网络过拟合的有效方法。
请注意,这两种dropout方法仅用于培训,在测试期间禁用。
NGCF Generalizes SVD++
svd++可以看作是没有高阶传播层的NGCF的一个特例,即一阶传播层。同时,禁用转换矩阵和非线性激活函数。然后,![]() 分别作为用户u和项目i的最终表示。我们将该简化模型称为NGCF-SVD,其表达式为:
分别作为用户u和项目i的最终表示。我们将该简化模型称为NGCF-SVD,其表达式为:
其中,两个衰减因子分别定义为![]() ,
,![]() 。
。
实验
数据集:Gowalla, Yelp2018, Amazon-book
RQ1:性能比较
不同稀疏度下的比较
RQ2:不同的超参数设置对实验的影响
层数的影响
嵌入传播层和层聚集机制的影响
dropout的影响
RQ3:高阶连通性的影响
随机抽取6个用户及其相关项目,可以看出NGCF-3(右图)出现了明显的聚类效果
参考
论文笔记:Neural Graph Collaborative Filtering(SIGIR 2019)
Neural Graph Collaborative Filtering--总结
![论文笔记 Neural Graph Collaborative Filtering [SIGIR 2019 ]_第1张图片](http://img.e-com-net.com/image/info8/fab3752d3c4c472b8ce9a3cc69adcddc.jpg)
![论文笔记 Neural Graph Collaborative Filtering [SIGIR 2019 ]_第2张图片](http://img.e-com-net.com/image/info8/78a2780e9af94e12984d715d05ec7537.jpg)
![论文笔记 Neural Graph Collaborative Filtering [SIGIR 2019 ]_第3张图片](http://img.e-com-net.com/image/info8/2e21d9105b8841df99cd373a7f520ad9.jpg)
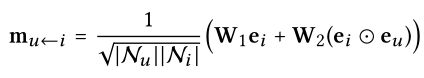
![论文笔记 Neural Graph Collaborative Filtering [SIGIR 2019 ]_第4张图片](http://img.e-com-net.com/image/info8/934c44ed1dee412eaf1c4767fd52d6a0.jpg)
![论文笔记 Neural Graph Collaborative Filtering [SIGIR 2019 ]_第5张图片](http://img.e-com-net.com/image/info8/5b76ecf0249f46a1b0483912c42c1259.jpg)
![论文笔记 Neural Graph Collaborative Filtering [SIGIR 2019 ]_第6张图片](http://img.e-com-net.com/image/info8/adbf2c915ecd434cb601a2c112b124d0.jpg)
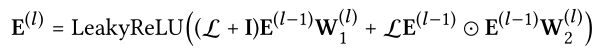
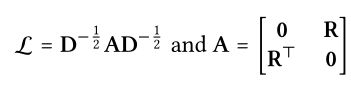
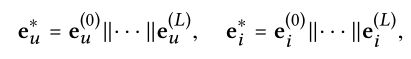
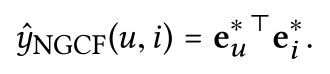

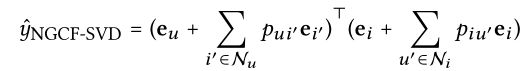
![论文笔记 Neural Graph Collaborative Filtering [SIGIR 2019 ]_第7张图片](http://img.e-com-net.com/image/info8/46a424a7e4594ccd80aa53e60a98fe25.jpg)
![论文笔记 Neural Graph Collaborative Filtering [SIGIR 2019 ]_第8张图片](http://img.e-com-net.com/image/info8/6076a16199804c699efae3180e3eedc1.jpg)
![论文笔记 Neural Graph Collaborative Filtering [SIGIR 2019 ]_第9张图片](http://img.e-com-net.com/image/info8/12fab4d1fc374b47a063d90f5f929ff9.jpg)
![论文笔记 Neural Graph Collaborative Filtering [SIGIR 2019 ]_第10张图片](http://img.e-com-net.com/image/info8/7d946667a5164b6cbbcae5c808a7ab73.jpg)
![论文笔记 Neural Graph Collaborative Filtering [SIGIR 2019 ]_第11张图片](http://img.e-com-net.com/image/info8/5ee590947bb5429e812dceb177e39e32.jpg)
![论文笔记 Neural Graph Collaborative Filtering [SIGIR 2019 ]_第12张图片](http://img.e-com-net.com/image/info8/0e017e7aa3984888b7087c5a9881ae7d.jpg)
![论文笔记 Neural Graph Collaborative Filtering [SIGIR 2019 ]_第13张图片](http://img.e-com-net.com/image/info8/1e1ae3dbd723497398692b00fcfcdac7.jpg)