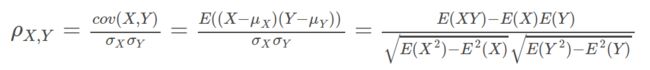Spark MLlib分布式机器学习源码分析：基本统计

​    Spark是一个极为优秀的大数据框架，在大数据批处理上基本无人能敌，流处理上也有一席之地，机器学习则是当前正火热AI人工智能的驱动引擎，在大数据场景下如何发挥AI技术成为优秀的大数据挖掘工程师必备技能。本文结合机器学习思想与Spark框架代码结构来实现分布式机器学习过程，希望与大家一起学习进步～

目录

1.概括统计

2.相关性系数

3.假设检验

4.随机数据生成

---

 

        本文采用的组件版本为：Ubuntu 19.10、Jdk 1.8.0_241、Scala 2.11.12、Hadoop 3.2.1、Spark 2.4.5。有关框架介绍和环境配置可以参考以下内容：    

    大数据处理框架Hadoop、Spark介绍

    linux下Hadoop安装与环境配置

    linux下Spark安装与环境配置

老规矩先开启一系列Hadoop、Spark服务与Spark-shell窗口：

 

1.概括统计

    MLlib支持RDD[Vector]列的概括统计，它通过调用Statistics的colStats方法实现。colStats返回一个MultivariateStatisticalSummary对象，这个对象包含列式的最大值、最小值、均值、方差等等。下面是一个应用例子：

import org.apache.spark.mllib.linalg.{Vector, Vectors}import org.apache.spark.mllib.stat.{MultivariateStatisticalSummary, Statistics}val observations = sc.parallelize(Seq( ,Vectors.dense(4.0,5.0,6.0))) // 一个向量RDD// 计算列统计量val summary: MultivariateStatisticalSummary = Statistics.colStats(observations)println(summary.mean) // 一个包含每列均值的dense向量println(summary.variance) // 列方差println(summary.numNonzeros) // 每列中的非零个数

2.相关性系数

    计算两个数据集的相关性是统计中的常用操作。在MLlib中提供了计算多个数据集两两相关的方法。目前支持的相关性方法有皮尔森(Pearson)相关和斯皮尔曼(Spearman)相关。

    Statistics提供方法计算数据集的相关性。根据输入的类型，两个RDD[Double]或者一个RDD[Vector]，输出将会是一个Double值或者相关性矩阵。下面是一个应用的例子。

import org.apache.spark.SparkContextimport org.apache.spark.mllib.linalg._import org.apache.spark.mllib.stat.Statisticsval seriesX = sc.parallelize(Array(1.0,2.0,3.0)) // 一个RDD序列val seriesY = sc.parallelize(Array(4.0,5.0,6.0)) // 必须具有与seriesX相同数量的分区和基数// 使用Pearson方法计算相关性。 输入“ spearman”作为Spearman的方法。 如果未指定方法，则默认使用Pearson方法。val correlation: Double = Statistics.corr(seriesX, seriesY, "pearson")val data = sc.parallelize(Seq(Vectors.dense(1.0,2.0,3.0),Vectors.dense(4.0,5.0,6.0))) // 注意每个向量是一行而不是一列// 使用Pearson方法计算相关矩阵。Spearman方法使用“ spearman”。如果未指定方法，则默认使用Pearson方法。val correlMatrix: Matrix = Statistics.corr(data, "pearson")

    皮尔森相关系数也叫皮尔森积差相关系数，是用来反映两个变量相似程度的统计量。或者说可以用来计算两个向量的相似度（在基于向量空间模型的文本分类、用户喜好推荐系统中都有应用）。

    当两个变量的线性关系增强时，相关系数趋于1或-1。正相关时趋于1，负相关时趋于-1。当两个变量独立时相关系统为0，但反之不成立。皮尔森相关系数计算公式如下：

 

    但是使用皮尔森线性相关系数有2个局限：首先，必须假设数据是成对地从正态分布中取得的；其次，数据至少在逻辑范围内是等距的。

 

    对于更一般的情况有其他的一些解决方案，Spearman秩相关系数就是其中一种。Spearman秩相关系数是一种无参数（与分布无关）检验方法，用于度量变量之间联系的强弱。在没有重复数据的情况下，如果一个变量是另外一个变量的严格单调函数，则Spearman秩相关系数就是+1或-1，称变量完全Spearman秩相关。注意这和Pearson完全相关的区别，只有当两变量存在线性关系时，Pearson相关系数才为+1或-1。公式如下：

 

3.假设检验

    假设检测是统计中有力的工具，它用于判断一个结果是否在统计上是显著的、这个结果是否有机会发生。spark.mllib目前支持皮尔森卡方检测。输入属性的类型决定是作拟合优度(goodness of fit)检测还是作独立性检测。拟合优度检测需要输入数据的类型是vector，独立性检测需要输入数据的类型是Matrix。

 

    spark.mllib也支持输入数据类型为RDD[LabeledPoint]，它用来通过卡方独立性检测作特征选择。Statistics提供方法用来作皮尔森卡方检测。下面是一个例子：

 

import org.apache.spark.mllib.linalg._import org.apache.spark.mllib.regression.LabeledPointimport org.apache.spark.mllib.stat.Statisticsimport org.apache.spark.mllib.stat.test.ChiSqTestResultimport org.apache.spark.rdd.RDD// 由事件的频率组成的向量val vec: Vector = Vectors.dense(0.1, 0.15, 0.2, 0.3, 0.25)// 计算拟合优度。如果没有提供第二个要测试的向量作为参数，则测试将针对均匀分布进行。val goodnessOfFitTestResult = Statistics.chiSqTest(vec)// 测试摘要，包括p值，自由度，测试统计量，使用的方法和原假设。println(s"$goodnessOfFitTestResult")// 权变矩阵 创建一个密集矩阵((1.0, 2.0), (3.0, 4.0), (5.0, 6.0))val mat: Matrix = Matrices.dense(3, 2, Array(1.0, 3.0, 5.0, 2.0, 4.0, 6.0))// 对输入列联矩阵进行Pearson独立性测试val independenceTestResult = Statistics.chiSqTest(mat)// 测试摘要，包括p值，自由度println(s"$independenceTestResult")val obs: RDD[LabeledPoint] = sc.parallelize(    Seq(      LabeledPoint(1.0, Vectors.dense(1.0, 0.0, 3.0)),      LabeledPoint(1.0, Vectors.dense(1.0, 2.0, 0.0)),      LabeledPoint(-1.0, Vectors.dense(-1.0, 0.0, -0.5)      )    )  ) // (label, feature) 对// 列联表是由原始（标签，要素）对构成的，用于进行独立性测试。 返回包含针对标签中每个功能的ChiSquaredTestResult的数组。val featureTestResults: Array[ChiSqTestResult] = Statistics.chiSqTest(obs)featureTestResults.zipWithIndex.foreach { case (k, v) =>  println(s"Column ${(v + 1)} :")  println(k)}  // 结果摘要

4.随机数据生成

    随机数据生成对于随机算法，原型设计和性能测试很有用。spark.mllib支持通过i.d生成随机RDD。从给定分布中得出的值：均匀，标准正态或泊松。

    RandomRDD提供了工厂方法来生成随机双RDD或矢量RDD。下面的示例生成一个随机双RDD，其值遵循标准正态分布N(0,1)，然后将其映射到N(1,4).

import org.apache.spark.SparkContextimport org.apache.spark.mllib.random.RandomRDDs._val u = normalRDD(sc, 1000000L, 10)// 生成包含100万个i.i.d的随机双RDD从标准正态分布“ N(0,1)”得出的值均匀分布在10个分区中。val v = u.map(x => 1.0 + 2.0 * x)println("mean of v = ",v.mean,"variance of v = ",v.variance)

5.核密度估计

    核密度估计是一种用于可视化经验概率分布的技术，无需假设要从中得出观察样本的特定分布。它计算在给定点集上评估的随机变量的概率密度函数的估计。它通过将特定点的经验分布的PDF表示为以每个样本为中心的正态分布PDF的平均值来实现此估计。

    KernelDensity提供了根据样本的RDD计算内核密度估计值的方法。下面的示例演示了如何执行此操作。

import org.apache.spark.mllib.stat.KernelDensityimport org.apache.spark.rdd.RDD// 一个简单RDDval data: RDD[Double] = sc.parallelize(Seq(1, 1, 1, 2, 3, 4, 5, 5, 6, 7, 8, 9, 9))// 使用样本数据和高斯核的标准差构造密度估计量val kd = new KernelDensity().setSample(data).setBandwidth(3.0)// 查找给定值的密度估计val densities = kd.estimate(Array(-1.0, 2.0, 5.0))

    Spark基本统计的内容至此结束，有关Spark的基础文章可参考前文：

    Spark MLlib分布式机器学习源码分析：矩阵向量

    Spark大数据分布式处理实战笔记（一）：快速开始

    Spark大数据分布式处理实战笔记（二）：RDD、共享变量

    Spark大数据分布式处理实战笔记（三）：Spark SQL

    Spark大数据分布式处理实战笔记（四）：Spark Streaming

    Spark大数据分布式机器学习处理实战

    Spark大数据分布式图计算处理实战

 

 

 

    参考链接：

    https://github.com/endymecy

    http://spark.apache.org/docs/latest/mllib-data-types.html

    https://www.cnblogs.com/zhangchaoyang/articles/2631907.html

 

 

历史推荐

“高频面经”之数据分析篇

“高频面经”之数据结构与算法篇

“高频面经”之大数据研发篇

“高频面经”之机器学习篇

“高频面经”之深度学习篇

爬虫实战：Selenium爬取京东商品

爬虫实战：豆瓣电影top250爬取

爬虫实战：Scrapy框架爬取QQ音乐

数据分析与挖掘

数据结构与算法

机器学习与大数据组件

欢迎关注，感谢“在看”，随缘稀罕~