- 【LeetCode 算法笔记】84. 柱状图中最大的矩形
Sardar_
算法leetcode笔记
目录问题描述暴力求解:栈问题描述给定n个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为1。求在该柱状图中,能够勾勒出来的矩形的最大面积。示例1:输入:heights=[2,1,5,6,2,3]输出:10解释:最大的矩形为图中红色区域,面积为10示例2:输入:heights=[2,4]输出:4提示:1int:area=0n=len(heights)foriinrange(n):
- 【LeetCode 算法笔记】739. 每日温度
Sardar_
算法leetcode笔记
目录问题描述暴力解法栈问题描述给定一个整数数组temperatures,表示每天的温度,返回一个数组answer,其中answer[i]是指对于第i天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用0来代替。示例1:输入:temperatures=[73,74,75,71,69,72,76,73]输出:[1,1,4,2,1,1,0,0]示例2:输入:temperatures=
- 【笔试题汇总】华为春招笔试题题解 2024-3-20
PXM的算法星球
大厂面试题华为面试数据结构算法
这里是paoxiaomo,一个现役ACMer,之后将会持续更新算法笔记系列以及笔试题题解系列本文章面向想打ICPC/蓝桥杯/天梯赛等程序设计竞赛,以及各个大厂笔试的选手感谢大家的订阅➕和喜欢有什么想看的算法专题可以私信博主(本文题面由清隆学长收集)01.K小姐的魔法药水问题描述K小姐是一位魔法师,她最近在研究一种神奇的魔法药水。这种药水由一系列魔法材料制成,每种材料都有一个正整数的魔法值。K小姐按
- 左神算法笔记———满足二叉搜索树的最大拓扑结构的大小
yaco
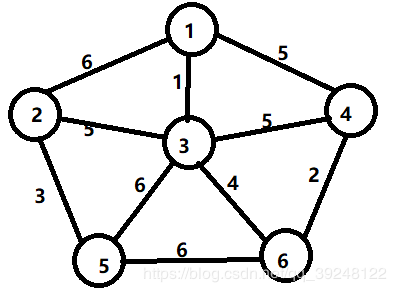
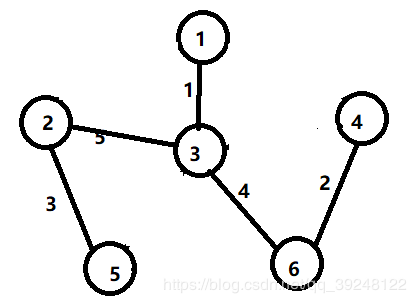
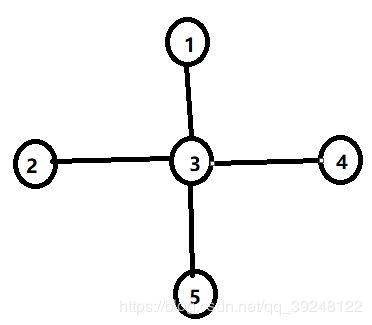
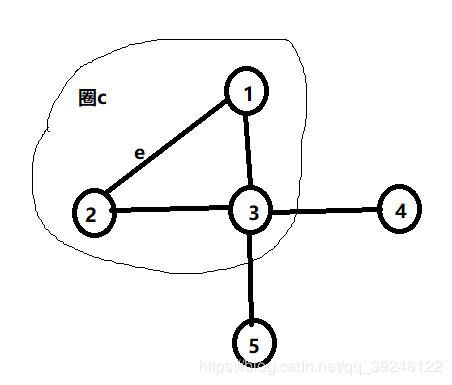
题目二叉树的拓扑结构概念:任何经过left和right指针,连成一片的节点,都叫一个拓扑结构。只要可以连在一起,都叫拓扑结构,区别与前一题的最大而二叉搜索子树。给定一棵二叉树的头节点head,请返回满足二叉搜索树条件的最大拓扑结构的大小。分析首先计算出以包含根节点的最大二叉搜索树的大小,实现方法可以遍历树中的各个节点,然后看根节点按照二叉搜索树的顺序是否可以走到这里来,如果可以,那么当前节点在二叉
- 24/8/17算法笔记 模仿学习算法
青椒大仙KI11
算法笔记学习
模仿学习(ImitationLearning,IL)算法是强化学习领域的一个分支,它关注于让智能体通过模仿专家的行为来学习任务。模仿学习通常用于学习复杂任务,尤其是当通过传统的强化学习算法直接学习效率较低或成本较高时。以下是一些常见的模仿学习算法:行为克隆(BehavioralCloning,BC):这是最直接的模仿学习方法,通过简单地训练一个策略网络来模仿专家的决策。通常使用监督学习的方法,将专
- 算法笔记:空间填充曲线
UQI-LIUWJ
算法笔记
空间填充曲线(Space-fillingcurve)是一种数学曲线,它可以无间断地覆盖一个多维空间的每一个点,从而实现从一维到多维的映射。用以解决连续与离散空间之间的映射问题。空间填充曲线的应用广泛,包括图像处理、地理信息系统、数据库索引等领域。计算机图形学和图像处理:在图像压缩和像素处理中,利用空间填充曲线的局部保持特性,可以优化图像的存储和访问效率。地理信息系统:空间填充曲线用于地理空间数据索
- 数学算法笔记
脑袋空空的Coduck君
笔记
1、平方差[蓝桥杯2023省A]平方差-洛谷考虑将公式化简,然后看x是由什么性质的数组成,该题中,从x奇偶性质入手,判断x可能的组成情况。题解:Welcome-LuoguSpilopelia2、完全平方数[蓝桥杯2021省AB2]完全平方数-洛谷P8754[蓝桥杯2021省AB2]完全平方数题解-洛谷专栏解题关键:1)唯一分解定理,对于任意一个数n,它都可以分解为若干个质数的乘积2)质因数分解,将
- Java面试八股文
翁正存
java
1.网络一文搞懂所有计算机网络面试题-知乎01我应该站在谁的肩膀上-OSIvsTCPIP模型2.Java面渣逆袭必看,面试题八股文Java基础、Java集合框架、Java并发编程、JVM、Spring、Redis、MyBatis、MySQL、操作系统、计算机网络、RocketMQ、分布式、微服务|二哥的Java进阶之路3.算法代码随想录配套JetBrains刷题插件|labuladong的算法笔记
- K-means(K均值聚类算法)算法笔记
Longlongaaago
机器学习机器学习kmeans算法
K-means(K均值聚类算法)算法笔记K-means算法,是比较简单的无监督的算法,通过设定好初始的类别k,然后不断循环迭代,将给定的数据自动分为K个类别。事实上,大家都知道K-means是怎么算的,但实际上,它是GMM(高斯混合模型)的一个特例,其而GMM是基于EM算法得来的,所以本文,将对K-means算法的算法思想进行分析。算法流程K-means算法的算法流程非常简单,可以从下图进行讲解(
- 剑指Offer算法笔记(Java)重建二叉树
十三幺Shisanyao
java算法剑指offerjava算法
5.重建二叉树描述给定节点数为n的二叉树的前序遍历和中序遍历结果,请重建出该二叉树并返回它的头结点。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建出如下图所示。提示:1.vin.length==pre.length2.pre和vin均无重复元素3.vin出现的元素均出现在pre里4.只需要返回根结点,系统会自动输出整颗树做答案对比数据
- java算法笔记
倔强青铜弟中弟
排序算法冒泡排序冒泡排序是最简单的排序之一了,其大体思想就是通过与相邻元素的比较和交换来把小的数交换到最前面。这个过程类似于水泡向上升一样,因此而得名。举个栗子:对5,3,8,6,4这个无序序列进行冒泡排序。1.首先从后向前冒泡,4和6比较,把4交换到前面,序列变成5,3,8,4,6。2.同理4和8交换,变成5,3,4,8,6,3和4无需交换。3.5和3交换,变成3,5,4,8,6,3.这样一次冒
- 算法刷题框架
洒水水儿
刷算法笔记算法
前言:最近积累了一些算法题量,正在刷东神的算法笔记,监督自己+记录下读后启发,顺便帮助道友们阅读数据结构这一部分老生常谈,数据的存储方式只有顺序存储和链式存储。最基本的数组和链表对应这两者,栈和队列都可以用顺序存储和链式存储实现;图的两种表示方法,邻接表就是链表,邻接矩阵就是二维数组;散列表就是通过散列函数把键映射到一个大数组里;树用数组实现就是堆,因为堆是一个完全二叉树,用数组存储不需要节点指针
- 算法笔记P67
Asteroid-110
算法笔记算法笔记
#includevoidswap(int*a,int*b){inttemp=*a;*a=*b;*b=temp;}intmain(){inta=1,b=2;int*p1=&a,*p2=&b;swap(p1,p2);printf("a=%d,b=%d",a,b);return0;}PS:对*和&的理解1.*:例如int*p的理解,就是p变量,只是是int*类型。一般这个p是地址,而*p是地址中的数值。
- C++开发基础知识
2024-01-0820:13星期一博客内容来自相关书籍和网站内容总结,仅供个人参考使用:笔者@StuBoo使用目录快速转到技术面试问题汇总、算法笔记1.C++语言基础1.1语言特性面向对象编程(OOP):C++支持面向对象编程,包括封装、继承和多态。通过类和对象,可以将数据和方法组织成单个单元,提高了代码的重用性和可维护性。标准模板库(STL):C++提供了STL,它包含了一组模板类和函数,例如
- 《算法笔记》3.1小节——入门模拟->简单模拟
木子李_0961
@[TOC]Contest100000575-《算法笔记》3.1小节——入门模拟->简单模拟1814ProblemA剩下的树来自http://codeup.cn/contest.php?cid=100000575#include#includeusingnamespacestd;inttree[10005]={0};intmain(){intL,M;while(scanf("%d%d",&L,&M
- 算法笔记------DP
_AC繁星S_
算法笔记算法
基础DP最大字段和:转移方程:f[i]=max(a[i],f[i-1]+a[i])对于要求字段起止位置的for(inti=1;i=0){f[i]=f[i-1]+a[i];}else{f[i]=a[i];ti=i;}if(f[i]>ans){ans=f[i];start=ti;ed=i;}}LIS模型暴力动态规划只采用最朴素的动态规划,复杂度O(N2)O(N^2)O(N2)for(inti=1;i#
- 算法笔记(一):位运算
Real返璞归真
算法C语言算法
0x3F0x3F3F3F3F在算法中是很有用的数值,他是满足以下两个条件的最大值:整数的两倍不超过0x7FFFFFFF,即int能表示的最大的整数。整数的每8位(每个字节)都是相同的。程序中经常使用memset(a,val,sizeof(a))初始化int数组,该语句把数值a(0x00~0xFF)填充到a的每个字节上。然而,1个int占用4个字,所以memset只能赋值出**“每8位相同”**的i
- 二维差分---三维差分算法笔记
摆烂小青菜
算法笔记算法笔记
文章目录一.二维差分构造差分二维数组二维差分算法状态dp求b[i][j]数组的二维前缀和图解二.三维前缀和与差分三维前缀和图解:三维差分核心公式图解:模板题一.二维差分给定一个原二维数组a[i][j],若要给a[i][j]中以(x1,y1)和(x2,y2)为对角线的子矩阵中每个数都加上一个常数c,暴力的做法时间复杂度为O(N^2),使用二维差分可以在O(1)的时间复杂度内完成该操作构造差分二维数组
- 算法笔记刷题日记——3.简单入门模拟 3.2 查找元素
哇哇哇哇池
ACM算法笔记算法笔记
刷题日记3.2查找元素B1041B1004B1028B1032A1011A1006A1036错题记录B1028人口普查某城镇进行人口普查,得到了全体居民的生日。现请你写个程序,找出镇上最年长和最年轻的人。这里确保每个输入的日期都是合法的,但不一定是合理的——假设已知镇上没有超过200岁的老人,而今天是2014年9月6日,所以超过200岁的生日和未出生的生日都是不合理的,应该被过滤掉。输入格式:输入
- 机器学习:遗传算法笔记
Ningbo_JiaYT
机器学习机器学习算法笔记
遗传算法(GeneticAlgorithm,GA)是一种基于自然选择和遗传机制的优化算法,其本质是通过模拟生物群体的演化过程来找到问题的最优解或接近最优解的解决方案,它最初由美国密歇根大学(UniversityofMichigan)的约翰·霍兰德(JohnHolland)教授于1967年提出。其灵感来源于达尔文的进化论,其中自然选择、遗传和变异是核心原理。目录基本原理1.基于种群2.染色体编码3.
- scikit-learn决策树算法笔记总结
python收藏家
决策树算法scikit-learn
1.scikit-learn决策树算法类库介绍scikit-learn决策树算法类库内部实现是使用了调优过的CART树算法,既可以做分类,又可以做回归。分类决策树的类对应的是DecisionTreeClassifier,而回归决策树的类对应的是DecisionTreeRegressor。两者的参数定义几乎完全相同,但是意义不全相同。下面就对DecisionTreeClassifier和Decisi
- Contest100000607 - 《算法笔记》7.3小节——数据结构专题(1)->链表处理
李霁明
算法笔记刷题笔记算法笔记数据结构链表
文章目录Contest100000607-《算法笔记》7.3小节——数据结构专题(1)->链表处理7.3链表处理7.3.1链表的概念7.3.2使用malloc函数或new运算符为链表结点分配内存空间7.3.3链表的基本操作链表的函数代码整理7.3.4静态链表PAT例题A1032SharingCodeup习题1326-ProblemA-算法2-8~2-11:链表的基本操作1870-ProblemB-
- 《算法笔记》7.3小节——数据结构专题(1)->链表处理
学代码不会秃
算法笔记数据结构链表算法
《算法笔记》7.3小节——数据结构专题(1)->链表处理问题A:算法2-8~2-11:链表的基本操作题目描述链表是数据结构中一种最基本的数据结构,它是用链式存储结构实现的线性表。它较顺序表而言在插入和删除时不必移动其后的元素。现在给你一些整数,然后会频繁地插入和删除其中的某些元素,会在其中某些时候让你查找某个元素或者输出当前链表中所有的元素。下面给你基本的算法描述:输入输入数据只有一组,第一行有n
- Z Algorithm(扩展KMP)算法笔记
吴代庄
算法笔记算法
假设给定一个s长度为的n字符串。那么这个字符串的z-function(“zet-function”)是一个长度为的数组,其中的-th元素等于最大字符数,从positioni开始,i与字符串的第一个字符n重合。换句话说,z[i]它是s字符串及其i-th后缀的最大通用前缀。注意:在本文中,为了避免歧义,我们将字符串视为0索引,即字符串的第一个字符具有索引0,最后一个n-1字符是。z函数的第一个元素通常
- 算法笔记刷题日记——刷题笔记规范
哇哇哇哇池
ACM算法笔记c++
1.后续Day在之前笔记中补充的内容用红色字体或加粗表示2.当日Day中的重要内容用亮黄色背景表示3.任务列表的使用方法当日已刷题错题
- 算法笔记刷题日记——3.简单入门模拟 3.1简单模拟
哇哇哇哇池
ACM算法笔记算法笔记
刷题日记3.1简单模拟此类题型根据题目描述进行代码的编写,考察代码能力,刷题记录如下:B1001B1032B1016B1026B1046B1008B1012B1018A1042A1046A1065B1010A1002A1009错题记录B1008数组元素循环右移问题一个数组_A_中存有_N_(>0)个整数,在不允许使用另外数组的前提下,将每个整数循环向右移_M_(≥0)个位置,即将_A_中的数据由(
- 状态压缩DP相关
刘先森222
算法
状态压缩动态规划学习笔记-AcWing状态压缩动态规划算法笔记(二)-AcWing【笔记】状压DP复习笔记-AcWing状态压缩dp-AcWing
- 算法笔记刷题日记——Day1 C_C++在ACM中的常用语法
哇哇哇哇池
ACM算法笔记算法笔记c语言
写在前面这学期选了ACM课,但平时缺乏练习,不怎么刷题,因此期末考试成绩并不理想。考虑到之后的考研复试中包含机试,且计试可以算是非常重要的印象分,因此我打算寒假刷一下算法笔记,备战3月初的PAT甲级和3月末的CCFCSP认证考试,为后续考研复习数据结构等也算是打下一个良好的基础。学习进度记录今日学习了算法笔记的章节2C/C++快速入门与章节3入门——简单模拟(1)的部分内容,本来打算略过章节2的部
- 算法笔记:树和二叉树基础
锐不可当cr
算法笔记系列
专题:树和二叉树基础内容来源:《挑战程序设计竞赛》(第2版)+《算法竞赛入门经典》(第2版)+网上资料整理汇总一、引入1.树是一种非线性的数据结构,用它能很好地描述有分支和层次特性的数据集合。树型结构在现实世界中广泛存在,如社会组织机构的组织关系图就可以用树型结构来表示。树在计算机领域中也有广泛应用,如在编译系统中,用树表示源程序的语法结构。在数据库系统中,树型结构是数据库层次模型的基础,也是各种
- 【算法笔记(六)】检索算法
ฅ˙Ꙫ˙ฅ599
python算法算法python数据结构
算法笔记(六)检索算法算法笔记(六)前言一、线性查找1.什么是线性查找2.需求规则3.人工图示演示4.代码实现二、二分查找1.什么是二分查找2.需求规则3.人工图示演示4.代码实现三.插值查找1.什么是插值查找2.需求规则3.人工图示演示4.代码实现四.斐波那契查找1.什么是斐波那契查找2.需求规则3.人工图示演示4.代码实现五.分块查找1.什么是分块查找2.需求规则3.人工图示4.代码实现六.哈
- jdk tomcat 环境变量配置
Array_06
javajdktomcat
Win7 下如何配置java环境变量
1。准备jdk包,win7系统,tomcat安装包(均上网下载即可)
2。进行对jdk的安装,尽量为默认路径(但要记住啊!!以防以后配置用。。。)
3。分别配置高级环境变量。
电脑-->右击属性-->高级环境变量-->环境变量。
分别配置 :
path
&nbs
- Spring调SDK包报java.lang.NoSuchFieldError错误
bijian1013
javaspring
在工作中调另一个系统的SDK包,出现如下java.lang.NoSuchFieldError错误。
org.springframework.web.util.NestedServletException: Handler processing failed; nested exception is java.l
- LeetCode[位运算] - #136 数组中的单一数
Cwind
java题解位运算LeetCodeAlgorithm
原题链接:#136 Single Number
要求:
给定一个整型数组,其中除了一个元素之外,每个元素都出现两次。找出这个元素
注意:算法的时间复杂度应为O(n),最好不使用额外的内存空间
难度:中等
分析:
题目限定了线性的时间复杂度,同时不使用额外的空间,即要求只遍历数组一遍得出结果。由于异或运算 n XOR n = 0, n XOR 0 = n,故将数组中的每个元素进
- qq登陆界面开发
15700786134
qq
今天我们来开发一个qq登陆界面,首先写一个界面程序,一个界面首先是一个Frame对象,即是一个窗体。然后在这个窗体上放置其他组件。代码如下:
public class First { public void initul(){ jf=ne
- Linux的程序包管理器RPM
被触发
linux
在早期我们使用源代码的方式来安装软件时,都需要先把源程序代码编译成可执行的二进制安装程序,然后进行安装。这就意味着每次安装软件都需要经过预处理-->编译-->汇编-->链接-->生成安装文件--> 安装,这个复杂而艰辛的过程。为简化安装步骤,便于广大用户的安装部署程序,程序提供商就在特定的系统上面编译好相关程序的安装文件并进行打包,提供给大家下载,我们只需要根据自己的
- socket通信遇到EOFException
肆无忌惮_
EOFException
java.io.EOFException
at java.io.ObjectInputStream$PeekInputStream.readFully(ObjectInputStream.java:2281)
at java.io.ObjectInputStream$BlockDataInputStream.readShort(ObjectInputStream.java:
- 基于spring的web项目定时操作
知了ing
javaWeb
废话不多说,直接上代码,很简单 配置一下项目启动就行
1,web.xml
<?xml version="1.0" encoding="UTF-8"?>
<web-app xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
xmlns="h
- 树形结构的数据库表Schema设计
矮蛋蛋
schema
原文地址:
http://blog.csdn.net/MONKEY_D_MENG/article/details/6647488
程序设计过程中,我们常常用树形结构来表征某些数据的关联关系,如企业上下级部门、栏目结构、商品分类等等,通常而言,这些树状结构需要借助于数据库完成持久化。然而目前的各种基于关系的数据库,都是以二维表的形式记录存储数据信息,
- maven将jar包和源码一起打包到本地仓库
alleni123
maven
http://stackoverflow.com/questions/4031987/how-to-upload-sources-to-local-maven-repository
<project>
...
<build>
<plugins>
<plugin>
<groupI
- java IO操作 与 File 获取文件或文件夹的大小,可读,等属性!!!
百合不是茶
类 File
File是指文件和目录路径名的抽象表示形式。
1,何为文件:
标准文件(txt doc mp3...)
目录文件(文件夹)
虚拟内存文件
2,File类中有可以创建文件的 createNewFile()方法,在创建新文件的时候需要try{} catch(){}因为可能会抛出异常;也有可以判断文件是否是一个标准文件的方法isFile();这些防抖都
- Spring注入有继承关系的类(2)
bijian1013
javaspring
被注入类的父类有相应的属性,Spring可以直接注入相应的属性,如下所例:1.AClass类
package com.bijian.spring.test4;
public class AClass {
private String a;
private String b;
public String getA() {
retu
- 30岁转型期你能否成为成功人士
bijian1013
成长励志
很多人由于年轻时走了弯路,到了30岁一事无成,这样的例子大有人在。但同样也有一些人,整个职业生涯都发展得很优秀,到了30岁已经成为职场的精英阶层。由于做猎头的原因,我们接触很多30岁左右的经理人,发现他们在职业发展道路上往往有很多致命的问题。在30岁之前,他们的职业生涯表现很优秀,但从30岁到40岁这一段,很多人
- 【Velocity四】Velocity与Java互操作
bit1129
velocity
Velocity出现的目的用于简化基于MVC的web应用开发,用于替代JSP标签技术,那么Velocity如何访问Java代码.本篇继续以Velocity三http://bit1129.iteye.com/blog/2106142中的例子为基础,
POJO
package com.tom.servlets;
public
- 【Hive十一】Hive数据倾斜优化
bit1129
hive
什么是Hive数据倾斜问题
操作:join,group by,count distinct
现象:任务进度长时间维持在99%(或100%),查看任务监控页面,发现只有少量(1个或几个)reduce子任务未完成;查看未完成的子任务,可以看到本地读写数据量积累非常大,通常超过10GB可以认定为发生数据倾斜。
原因:key分布不均匀
倾斜度衡量:平均记录数超过50w且
- 在nginx中集成lua脚本:添加自定义Http头,封IP等
ronin47
nginx lua csrf
Lua是一个可以嵌入到Nginx配置文件中的动态脚本语言,从而可以在Nginx请求处理的任何阶段执行各种Lua代码。刚开始我们只是用Lua 把请求路由到后端服务器,但是它对我们架构的作用超出了我们的预期。下面就讲讲我们所做的工作。 强制搜索引擎只索引mixlr.com
Google把子域名当作完全独立的网站,我们不希望爬虫抓取子域名的页面,降低我们的Page rank。
location /{
- java-3.求子数组的最大和
bylijinnan
java
package beautyOfCoding;
public class MaxSubArraySum {
/**
* 3.求子数组的最大和
题目描述:
输入一个整形数组,数组里有正数也有负数。
数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和。
求所有子数组的和的最大值。要求时间复杂度为O(n)。
例如输入的数组为1, -2, 3, 10, -4,
- Netty源码学习-FileRegion
bylijinnan
javanetty
今天看org.jboss.netty.example.http.file.HttpStaticFileServerHandler.java
可以直接往channel里面写入一个FileRegion对象,而不需要相应的encoder:
//pipeline(没有诸如“FileRegionEncoder”的handler):
public ChannelPipeline ge
- 使用ZeroClipboard解决跨浏览器复制到剪贴板的问题
cngolon
跨浏览器复制到粘贴板Zero Clipboard
Zero Clipboard的实现原理
Zero Clipboard 利用透明的Flash让其漂浮在复制按钮之上,这样其实点击的不是按钮而是 Flash ,这样将需要的内容传入Flash,再通过Flash的复制功能把传入的内容复制到剪贴板。
Zero Clipboard的安装方法
首先需要下载 Zero Clipboard的压缩包,解压后把文件夹中两个文件:ZeroClipboard.js
- 单例模式
cuishikuan
单例模式
第一种(懒汉,线程不安全):
public class Singleton { 2 private static Singleton instance; 3 pri
- spring+websocket的使用
dalan_123
一、spring配置文件
<?xml version="1.0" encoding="UTF-8"?><beans xmlns="http://www.springframework.org/schema/beans" xmlns:xsi="http://www.w3.or
- 细节问题:ZEROFILL的用法范围。
dcj3sjt126com
mysql
1、zerofill把月份中的一位数字比如1,2,3等加前导0
mysql> CREATE TABLE t1 (year YEAR(4), month INT(2) UNSIGNED ZEROFILL, -> day
- Android开发10——Activity的跳转与传值
dcj3sjt126com
Android开发
Activity跳转与传值,主要是通过Intent类,Intent的作用是激活组件和附带数据。
一、Activity跳转
方法一Intent intent = new Intent(A.this, B.class); startActivity(intent)
方法二Intent intent = new Intent();intent.setCla
- jdbc 得到表结构、主键
eksliang
jdbc 得到表结构、主键
转自博客:http://blog.csdn.net/ocean1010/article/details/7266042
假设有个con DatabaseMetaData dbmd = con.getMetaData(); rs = dbmd.getColumns(con.getCatalog(), schema, tableName, null); rs.getSt
- Android 应用程序开关GPS
gqdy365
android
要在应用程序中操作GPS开关需要权限:
<uses-permission android:name="android.permission.WRITE_SECURE_SETTINGS" />
但在配置文件中添加此权限之后会报错,无法再eclipse里面正常编译,怎么办?
1、方法一:将项目放到Android源码中编译;
2、方法二:网上有人说cl
- Windows上调试MapReduce
zhiquanliu
mapreduce
1.下载hadoop2x-eclipse-plugin https://github.com/winghc/hadoop2x-eclipse-plugin.git 把 hadoop2.6.0-eclipse-plugin.jar 放到eclipse plugin 目录中。 2.下载 hadoop2.6_x64_.zip http://dl.iteye.com/topics/download/d2b
- 如何看待一些知名博客推广软文的行为?
justjavac
博客
本文来自我在知乎上的一个回答:http://www.zhihu.com/question/23431810/answer/24588621
互联网上的两种典型心态:
当初求种像条狗,如今撸完嫌人丑
当初搜贴像条犬,如今读完嫌人软
你为啥感觉不舒服呢?
难道非得要作者把自己的劳动成果免费给你用,你才舒服?
就如同 Google 关闭了 Gooled Reader,那是
- sql优化总结
macroli
sql
为了是自己对sql优化有更好的原则性,在这里做一下总结,个人原则如有不对请多多指教。谢谢!
要知道一个简单的sql语句执行效率,就要有查看方式,一遍更好的进行优化。
一、简单的统计语句执行时间
declare @d datetime ---定义一个datetime的变量set @d=getdate() ---获取查询语句开始前的时间select user_id
- Linux Oracle中常遇到的一些问题及命令总结
超声波
oraclelinux
1.linux更改主机名
(1)#hostname oracledb 临时修改主机名
(2) vi /etc/sysconfig/network 修改hostname
(3) vi /etc/hosts 修改IP对应的主机名
2.linux重启oracle实例及监听的各种方法
(注意操作的顺序应该是先监听,后数据库实例)
&nbs
- hive函数大全及使用示例
superlxw1234
hadoophive函数
具体说明及示例参 见附件文档。
文档目录:
目录
一、关系运算: 4
1. 等值比较: = 4
2. 不等值比较: <> 4
3. 小于比较: < 4
4. 小于等于比较: <= 4
5. 大于比较: > 5
6. 大于等于比较: >= 5
7. 空值判断: IS NULL 5
- Spring 4.2新特性-使用@Order调整配置类加载顺序
wiselyman
spring 4
4.1 @Order
Spring 4.2 利用@Order控制配置类的加载顺序
4.2 演示
两个演示bean
package com.wisely.spring4_2.order;
public class Demo1Service {
}
package com.wisely.spring4_2.order;
public class