kaggle：泰坦尼克生存预测（ R语言机器学习分类算法）

 

  本文在基本的多元统计分析技术理论基础上，结合机器学习基本模型，选择Kaggle（数据建模竞赛网站）的入门赛——Titanic生存预测作为实战演练，较为完整地呈现了数据建模的基本流程和思路。采用的模型有逻辑回归，决策树，SVM支持向量机以及进阶的集成学习方法——Boosting和RandomForest。 在建立模型后基于混淆矩阵的模型评估方法给出了Titanic生存预测的基本结论。 该数据集训练集一共包含891条记录，12个属性，其中Survived为目标属性，测试集包含481条记录，数据说明如下：

变量名	含义
Survived	是否幸存
Name	乘客姓名
Sex	乘客性别
Age	乘客年龄
SibSp	乘客随行的兄弟姐妹数量
Parch	乘客随行的父母/兄弟数量
Ticket	票号
Fare	票价
Cabin	船舱
Pclass	乘客等级(1=头等 2=二等3=三等)
Embarked	登船港口（C = Cherbourg S = Southampton Q = Queenstown）

二、数据理解

2.1原始数据质量

由数据质量表可知，训练集共有891条记录，年龄字段存在19.87%的缺失值（177条）,可根据姓名字段进行分组均值(或者中位数）填补,且Survived，Pclass，Se，Embarked为类别型变量，其他数据完整。

表1 数据质量表（总表）

变量名	数据类型	不同值个数	空值个数	空值比例	有值个数	有值比例
PassengerId	numeric	891	0	0%	891	100%
Survived	numeric	2	0	0%	891	100%
Pclass	numeric	3	0	0%	891	100%
Name	character	891	0	0%	891	100%
Sex	character	2	0	0%	891	100%
Age	numeric	89	177	19.87%	714	80.13%
SibSp	numeric	7	0	0%	891	100%
Parch	numeric	7	0	0%	891	100%
Ticket	character	681	0	0%	891	100%
Fare	numeric	248	0	0%	891	100%
Cabin	character	148	687	77.10%	204	22.90%
Embarked	character	4	2	0.22%	889	99.78%

Fare（船费）存在15笔零值，可能是异常值，船票的票价和乘客等级有关，因此在数据处理部分可根据Pclass信息分组来做均值填补.

表2 数据质量表（数值型）

变量名	Min	Max	Mean	StDev	M-3	M+3
Age	0.42	80	29.70	3.8	18.3	41.1
Fare	0.00	512	32.20	7.0	11.1	53.4
SibSp	0.00	8	0.52	1.0	-2.6	3.7
Parch	0.00	6	0.38	0.9	-2.3	3.1

Embarked（上船港口）存在2个空字符，导入时已经将空字符替换为NA，因此在数据处理部分可用众数填充

表3 数据质量表（类别型）

变量名	Level	Count
Survived	0:1	549:342
Pclass	1:2:3	216:184:491
Sex	female:male	314:577
Embarked	C:Q:S	168:77:644

2.2数据类型转换

进行数据类型转换，将分类变量转为因子型

2.3探索性分析

1.总体幸存情况：38%(549名)乘客遇难，62%（342名）乘客获救

 

 

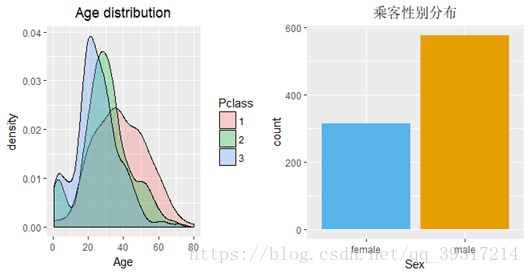
2.总体年龄/性别分布：去掉缺失值后的分析结果表明头等舱及二等舱的年龄均值大于三等舱，各等级船舱年龄均值为头等舱38岁，二等舱30岁，三等舱25岁,乘客中男性居多占比达到65%，所以男性遇难率高也有样本本身占比高的因素。

 

 

3.不同等级生存情况 ：不同等级的幸存率为头等舱63%，二等舱47%，三等舱24%,且泰坦尼克号和别的客轮一样，将存放救生艇的区域安排在了头等舱和二等舱附近，以降低富人和中产阶级乘客对航海风险的担心下水逃生的安排也保持了这个相同的逻辑，即头等舱、二等舱优先。

表4 不同等级船舱乘客幸存情况

Survived	1	2	3
0	0.37	0.53	0.76
1	0.63	0.47	0.24

 

 

 

4.不同船舱等级儿童生存情况 ：医学界一般以0-14岁的儿童作为儿科研究对象，因此此处将年龄在14岁及以下的定为儿童，分析其生存情况。数据显示儿童幸存率为58%,对儿童按照不同船舱等级进行分组，发现船舱等级的不同影响儿童的幸存情况，头等舱及二等舱儿童的幸存率为96%（24名儿童获救，仅有1名儿童遇难）而三等舱儿童幸存率为42%（22名儿童获救，31名儿童遇难），可见乘客生存最重要的影响因素还是船舱等级 。

表5 各船舱等级儿童幸存

Pclass	0	1
高等舱	0.04	0.96
三等舱	0.58	0.42

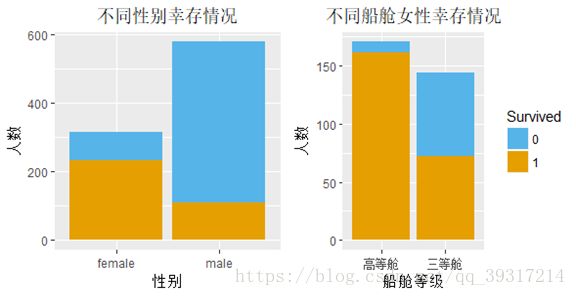
5.不同性别生存情况分析 ：女性幸存率为65%，其中头等舱及二等舱女性的幸存率为95%（161名女性获救，9名女性遇难）而三等舱女性幸存率为50%（72名女性获救，72名女性遇难）

第三部分：数据准备

3.1训练集数据清洗

对照2.1数据质量表及表属性统计的信息对缺失值及异常值进行清洗处理。年龄字段有177个缺失，缺失率19%，影响较大，因此需要谨慎处理，通过查看年龄的分布图发现右偏，观察字段发现年龄和姓名里的称谓(Mrs.Mr.Miss.Dr)有关，因此选对姓名字段进行文本分析，将称谓的模式找出来，进行分组后用不同称谓年龄的中位数对缺失的年龄进行填补。船费为0的情况则可能是误填或者因缺失而登记为0，船费和乘客的船舱等级有关，头等舱的价格高于二等舱高于三等舱，因此根据船舱等级对船费为0的记录进行填补。而登船口岸和幸存情况没有太大关系，只有2个缺失，因此用众数进行填补。

表6 不同称谓年龄的中位数

Mr	Mrs	Dr	Miss	Master
30	35	46	21	3.5

3.2测试集数据清洗

训练集共有418条记录，年龄字段存在20.57%的缺失值（86条）,处理方法与测试集相同.Fare存在2笔零值，可能是异常值，1笔缺失，Fare为缺失的1个值根据仓位等级的中位数进行填补(此处只有三等舱存在1个缺失，但测试集中无三等舱，因此用训练集的三等舱插补。

3.3 筛选建模属性

进行建模的属性筛选，因此乘客ID，姓名，票号，座位号，对模型拟合没有意义，此处进行剔除，最终参与建模的数据质量表如下。

表7 数据质量表（总表）

变量名	数据类型	不同值个数	空值个数	空值比例	有值个数	有值比例
Survived	numeric	2	0	0%	891	100%
Pclass	numeric	3	0	0%	891	100%
Sex	numeric	2	0	0%	891	100%
Age	numeric	90	0	0%	891	100%
SibSp	numeric	7	0	0%	891	100%
Parch	numeric	7	0	0%	891	100%
Fare	numeric	249	0	0%	891	100%
Embarked	numeric	3	0	0%	891	100%

 

表8 数据质量表（数值型）

变量名	Min	Max	Mean	StDev	M-3	M+3
Age	0.42	80	29.39	3.6	18.5	40.3
Fare	4.01	512	32.67	7.0	11.5	53.8
SibSp	0.00	8	0.52	1.0	-2.6	3.7
Parch	0.00	6	0.38	0.9	-2.3	3.1

表9 数据质量表（类别型）

变量名	Level	Count
Survived	0:1	549:342
Pclass	1:2:3	216:184:491
Sex	female:male	314:577
Embarked	C:Q:S	168:77:646

3.4 进行数据抽样

将数据集分为训练集和测试集，目的是实现在训练集上训练模型，在验证测试集上验证模型的准确率，对模型进行评估

 

第四部分：建立模型

4.1逻辑回归

Logistic回归模型将适用于因变量为二分类的分类变量或某事件的发生率，这里Survived是否幸存作为目标变量，用逻辑回归得到目标变量的概率值。

4.2决策树

采用CART算法，基于Gini指标选择属性，用全部变量建树，根据十折交叉验证的复杂度参数及误差进行后剪枝，最后建立决策树，对决策规则进行可视化，决策树绘图如下。

4.3随机森林

采用组合的方式，加入随机性，基于不同的属性及样本选择来建立决策树，此处建立500个基分类器，进行组合投票。随机森林对噪声有很好的鲁棒性，运行速度比Adaboost更快，随机森林通过随机和组合来减少决策树之间的相关性，改善组合分类器的繁华误差。从随机森林中提取的各属性重要性从高到低依次为性别、船费、年龄、乘客随行的兄弟姐妹数量、乘客随行的父母/兄弟数量。

变量名	MeanDecreaseGini
Sex	74
Fare	47
Age	41
SibSp	21
Parch	12
Fare	11
Embarked	11

4.4支持向量机

支持向量机可以将线性不可分的分类问题映射到高维去解决，找到一个最优平面，最大化边缘，可以避免维灾难，同时可以减少泛化误差。

4.5用boosting提升算法来生成组合模型

Boosting是集成学习的一种，生成基分类器的过程是串行的，是一个迭代的过程，用来自适应地改变训练样本的分布，使得基分类器聚焦在那些很难分的样本上。此处采用Adaboost（提升算法最著名的一种算法）来训练模型，Adaboost基于分类错误样本来更新训练样本的权值。

第五部分：模型评估及选择

利用混淆矩阵得到5种模型的精确度，综合来看，SVM支持向量机表现最好，准确率为84%，因此采用SVM进行预测。

表10 模型评估表

	Logit	tree	RandomForst	SVM	Adaboost
sensitivity	0.64	0.61	0.61	0.69	0.64
specificity	0.88	0.94	0.95	0.93	0.87
positivive predictive value	0.76	0.86	0.87	0.85	0.74
negtive predictive value	0.80	0.80	0.80	0.83	0.80
accuracy	0.79	0.82	0.82	0.84	0.78
F1	0.70	0.71	0.72	0.76	0.69

第六部分：生存预测

用SVM对测试集的数据进行预测将预测结果添加到数据中，预览如下：

表11 预测结果

Pclass	Sex	Age	SibSp	Parch	Fare	Embarked	Survival
3	male	34	0	0	7.8	Q	0
3	female	47	1	0	7.0	S	1
2	male	62	0	0	9.7	Q	0
3	male	27	0	0	8.7	S	0
3	female	22	1	1	12.3	S	1
3	male	14	0	0	9.2	S	0
3	female	30	0	0	7.6	Q	1
2	male	26	1	1	29.0	S	0
3	female	18	0	0	7.2	C	1
3	male	21	2	0	24.1	S	0

 项目代码如下：

# kaggle--Titanic:Machine Learning from disaster
#预备部分：函数定义
#1.数据质量表
data_quality<- function(x){
  mode_data<- c()
  diff_data<- c()
  na_data<- c()
  na_datar<- c()
  fna_data<- c()
  fna_datar<- c()
  for (i in 1:ncol(x)){
    mode_data<-c(mode_data,mode(x[,i]))
    diff_data<- c(diff_data,length(unique(x[[i]])))
    na_data<- c(na_data,sum(is.na(x[,i])))
    nr<- paste(round(na_data[i]/nrow(x),4)*100,"%",sep = "")
    na_datar<- c(na_datar,nr)
    fna_data<- c(fna_data,sum(!is.na(x[,i])))
    fnr<- paste(round(fna_data[i]/nrow(x),4)*100,"%",sep = "")
    fna_datar<- c(fna_datar,fnr)
  }
  result<- rbind(mode_data,diff_data,na_data,na_datar,fna_data,fna_datar)
  colnames(result)<- colnames(x)
  rownames(result)<-c("数据类型","不同值个数","空值个数","空值比例","有值个数","有值比例")
  result<- as.data.frame(result)
  # print(ls(envir = parent.frame(n=1)))
  return(result)
} 
#2.类别型变量转换
data_transform<- function(x){
  for (i in 1:ncol(x))
    if(length(unique(x[[i]])) < 5){
      x[[i]]<-as.factor(x[[i]])
    }
  return(x)
}
#3.数值型/类别型-数据质量表
quality_numeric<- function(x){
  m1<-c()
  m2<-c()
  m3<-c()
  stdev<-c()
  m3_r<-c()
  m3_l<-c()
  options(digits=2)
  for (i in 1:ncol(x)){
    m1<- c(m1,min(x[[i]],na.rm = T))
    m2<- c(m2,max(x[[i]],na.rm = T))
    m3<- c(m3,mean(x[[i]],na.rm = T))
    stdev<- c(stdev,sqrt(sd(x[[i]],na.rm = T)))
    m3_r<-c(m3_r,m3[i]-3*stdev[i])
    m3_l<-c(m3_l,m3[i]+3*stdev[i])
  }
  result<- cbind(m1,m2,m3,stdev,m3_r,m3_l)
  rownames(result)<- names(x)
  colnames(result)<- c("Min","Max","Mean","StDev","M-3","M+3")
  result<- as.data.frame(result)
  return(result)
}
quality_factor<- function(x){
  Level<- c()
  Count<- c()
  for (i in 1:ncol(x)){
    r<- table(x[[i]])
    le<- c()
    co<- c()
    for (k in 1:length(r)){
      le<- paste(le,names(r)[k],sep = ":")
      co<- paste(co,r[k],sep = ":")}
    Level<- rbind(Level,le)
    Count<- rbind(Count,co)}
  result<- cbind(Level,Count)
  rownames(result)<-names(x)
  colnames(result)<- c("Level","Count")
  result<- as.data.frame(result)
  return(result)
}
#4.模型评估
performance<- function(table,n=2){
  if(!all(dim(table)==c(2,2)))
    stop("Must be a 2*2 table")
  tn=table[1,1]
  fn=table[2,1]
  tp=table[2,2]
  fp=table[1,2]
  sensitivity=tp/(tp+fn)
  specificity=tn/(tn+fp)
  ppp=tp/(tp+fp)
  npp=tn/(tn+fn)
  hitrate=(tp+tn)/(tp+tn+fp+fn)
  F1=2*sensitivity*ppp/(ppp+sensitivity)
  result<- rbind(sensitivity,specificity,ppp,npp,hitrate,F1)
  rownames(result)<- c("sensitivity","specificity","positivive predictive value","negtive predictive value","accuracy","F1")
  colnames(result)<- c("model")
  return(result)
}

#5.安装包
#字符处理
library(stringr)
#缺失值可视化
library(Amelia)
library(VIM)
#画图
library(ggplot2)
#画图组合
# install.packages("devtools")
# library(devtools)
# install_github("easyGgplot2", "kassambara")
library(easyGgplot2)

#--------第一部分：读取数据--------####
setwd("D:\\桃子的数据\\Titani Machine Learning from Disaster")
train<- read.csv("train.csv",header = TRUE,sep = ",",stringsAsFactors = FALSE,na.strings = c("NA",""))
test<- read.csv("test.csv",header = TRUE,sep = ",",stringsAsFactors = FALSE,na.strings = c("NA",""))


#--------第二部分：数据理解--------####
#----2.1查看原始数据质量####
#数据质量表（总表）
train_data_quality<- data_quality(train)
train_data_quality 
#---由数据质量表可知，训练集共有891条记录，年龄字段存在19.87%的缺失值（177条）,可根据姓名字段进行均值(或者回归）填补,且Survived,Pclass,Sex,Sibsp,Parch,Embarked为分类型变量，其他数据完整
#数据质量表（数值型）
numeric_train<- train[,c("Age","Fare","SibSp","Parch")]
quality_numeric_train<-quality_numeric(numeric_train)
quality_numeric_train
length(train$Fare[which(train$Fare==0)])
##---Fare存在15笔零值，可能是异常值，船票的票价和乘客等级有关，因此可根据Pclass信息来做均值填补
# library(rcompanion)
# plotNormalHistogram(numeric_train[,1])
# plotNormalHistogram(numeric_train[,2])
#数据质量表（类别型）
factor_train<- train[,c("Survived","Pclass","Sex","Embarked")]
quality_factor_train<- quality_factor(factor_train)
quality_factor_train
table(train$Embarked,useNA = "always")
##---Embarked（上船港口）存在2个空字符，导入时已经将空字符替换为NA，后面数据处理可用众数填充

#缺失数据可视化
# library("Amelia")
# missmap(train,main = "Missing Map")

#----2.2数据类型转换####
# (类别型变为因子型：函数设定小于5个水平都被转为因子型)
train<- data_transform(train)
str(train)

#----2.3探索性分析####
#2.3.1总体幸存情况
options(digits = 2)
ggplot(train,aes(x=Survived,fill=Survived))+geom_bar()
+labs(title="总体幸存情况",x="是否幸存",y="人数")
+scale_fill_manual(values=c("#999999", "#E69F00"))
+theme(plot.title = element_text(hjust = 0.5),legend.position = "none") 
prop.table(table(train$Survived))
#38%的乘客遇难，62的乘客获救

#2.3.2总体年龄/性别分布 
plot1<-ggplot(train,aes(x=Age,fill=Pclass))+geom_density(alpha=.3)+labs(title="Age distribution")+theme(plot.title = element_text(hjust = 0.5)) 
plot2<-ggplot(train,aes(x=Sex,fill=Sex))+geom_bar()+labs(title="乘客性别分布")+scale_fill_manual(values=c("#56B4E9", "#E69F00"))+theme(plot.title = element_text(hjust = 0.5),legend.position = "none") 
ggplot2.multiplot(plot1,plot2,cols=2)

train_age<- train[!is.na(train$Age),]
tapply(train_age$Age,train_age$Pclass,mean)
prop.table(table(train$Sex))
#去掉缺失值后的分析结果表明头等舱及二等舱的年龄均值大于三等舱，各等级船舱的年龄均值如下：头等舱38岁，二等舱30岁，三等舱25岁,乘客中男性居多占比达到65%，所以男性遇难率高也有样本占比高的原因。

# 2.3.3各等级生存情况
ggplot(train,aes(x=Pclass,fill=Survived))+geom_bar()+labs(title="Survival of different Pclass")+scale_fill_manual(values=c("#999999", "#E69F00"))+theme(plot.title = element_text(hjust = 0.5))
prop.table(table(train$Survived,train$Pclass),margin = 2)
#不同等级的幸存率为头等舱63%，二等舱47%，三等舱24%,
#且泰坦尼克号和别的客轮一样，将存放救生艇的区域安排在了头等舱和二等舱附近，以降低富人和中产阶级乘客对航海风险的担心
# 下水逃生的安排也保持了这个相同的逻辑，即头等舱、二等舱优先，而不是后来盛传的“妇女儿童优先

# 2.3.4各年龄生存情况
ggplot(train,aes(x=Age))+geom_density()+labs(title="Age distribution")+theme(plot.title = element_text(hjust = 0.5))
# 医学界一般以0-14岁的儿童作为儿科研究对象，因此此处将年龄在14岁及以下的定为儿童，分析其生存情况
train_age_14<- train_age[which(train_age$Age <= 14),]
train_age_14$pclass14<- ""
train_age_14$pclass14[train_age_14$Pclass==1 | train_age_14$Pclass==2]<- "高等舱"
train_age_14$pclass14[train_age_14$Pclass==3]<- "三等舱"
#交叉表
table(train_age_14$Survived)
table(train_age_14$pclass14,train_age_14$Survived)
prop.table(table(train_age_14$Survived))
prop.table(table(train_age_14$pclass14,train_age_14$Survived),margin = 1)
#作图
plot3<-ggplot(train_age_14,aes(x=Survived,fill=Survived))+geom_bar()+labs(title="儿童幸存情况（0-14岁）",x="是否幸存",y="人数")+scale_fill_manual(values=c("#999999", "#E69F00"))+theme(plot.title = element_text(hjust = 0.5),legend.position = "none")
plot4<-ggplot(train_age_14,aes(x=pclass14,fill=Survived))+geom_bar()+labs(title="不同船舱儿童幸存情况（0-14岁）",x="船舱等级",y="人数")+scale_fill_manual(values=c("#999999", "#E69F00"))+theme(plot.title = element_text(hjust = 0.5))
ggplot2.multiplot(plot3,plot4,cols=2)
#儿童幸存率为58%,头等舱及二等舱儿童的幸存率为96%（24名儿童获救，仅有1名儿童遇难）
# 而三等舱儿童幸存率为42%（22名儿童获救，31名儿童遇难），可见乘客生存最重要的影响因素还是船舱等级

# 2.3.5性别生存情况分析
train_female<- train[which(train$Sex=="female"),]
train_female$pclass_female<- ""
train_female$pclass_female[train_female$Pclass==1 | train_female$Pclass==2]<- "高等舱"
train_female$pclass_female[train_female$Pclass==3]<- "三等舱"
#交叉表
table(train_female$Survived)
table(train_female$pclass_female,train_female$Survived)
prop.table(table(train$Sex))
prop.table(table(train_female$Survived,train_female$pclass_female),margin = 2)
#作图
plot5<-ggplot(train,aes(x=Sex,fill=Survived))+geom_bar()+labs(title="不同性别幸存情况",x="性别",y="人数")+scale_fill_manual(values=c("#56B4E9", "#E69F00"))+theme(plot.title = element_text(hjust = 0.5),legend.position = "none")
plot6<-ggplot(train_female,aes(x=pclass_female,fill=Survived))+geom_bar()+labs(title="不同船舱女性幸存情况",x="船舱等级",y="人数")+scale_fill_manual(values=c("#56B4E9", "#E69F00"))+theme(plot.title = element_text(hjust = 0.5))
ggplot2.multiplot(plot5,plot6,cols=2)
#女性幸存率为65%，其中头等舱及二等舱女性的幸存率为95%（161名女性获救，9名女性遇难）
# 而三等舱女性幸存率为50%（72名女性获救，72名女性遇难）

#决策树属性重要性





#--------第三部分：数据准备--------####

#----3.1训练集数据清洗----####

#----3.1.1空字符串处理Embarked
table(train$Embarked,useNA = "always")
train$Embarked[which(is.na(train$Embarked))] <- 'S'
table(train$Embarked,useNA = "always")

#----3.1.2异常值处理Fare
#Fare为0 的值根据仓位等级的中位数进行填补
a1<-tapply(train$Fare,train$Pclass,median)
train[which(train$Fare==0&train$Pclass==1),"Fare"]<- a1[[1]]
train[which(train$Fare==0&train$Pclass==2),"Fare"]<- a1[[2]]
train[which(train$Fare==0&train$Pclass==3),"Fare"]<- a1[[3]]

#----3.1.3.处理缺失值---Age根据称呼用中位数插补年龄
# library(stringr)
table_words <- table(unlist(strsplit(train$Name,"\\s+")))  #table是为了对词进行计数
sort(table_words [grep('\\.',names(table_words))],decreasing = TRUE) #将含有.的词（这些代表称呼）提取出来排序
tb <- cbind(train$Age,str_match(train$Name,"[a-zA-Z]+\\.")) #（+代表一个或多个）
table(tb[is.na(tb[,1]),2])
median.mr <- median(train$Age[grepl("Mr\\.",train$Name) & !is.na(train$Age)]) #方法一grepl返回布尔值，grep返回行号
median.mrs <- median(train$Age[grepl("Mrs\\.",train$Name)],na.rm = T) #方法二:加上na.rm=
median.dr <- median(train$Age[grepl("Dr\\.",train$Name) & !is.na(train$Age)])
median.miss <- median(train$Age[grepl("Miss\\.",train$Name) & !is.na(train$Age)])
median.master <- median(train$Age[grepl("Master\\.",train$Name) & !is.na(train$Age)])
cbind(median.mr,median.mrs,median.dr,median.miss,median.master)
#中位数填补
train$Age[grepl("Mr\\.",train$Name) & is.na(train$Age)] <- median.mr
train$Age[grepl("Mrs\\.",train$Name) & is.na(train$Age)] <- median.mrs
train$Age[grepl("Dr\\.",train$Name) & is.na(train$Age)] <- median.dr
train$Age[grepl("Miss\\.",train$Name) & is.na(train$Age)] <- median.miss
train$Age[grepl("Master\\.",train$Name) & is.na(train$Age)] <- median.master
#处理后缺失值可视化
missmap(train,main = "Missing Map")
aggr(train,numbers = TRUE)
#--训练集已经不存在缺失值,存疑点：3等舱的年龄均值处理之后分布变成两个峰值，可能是由于缺失较多，且mr男性32岁填充较多。
ggplot(train,aes(x=Age,fill=Pclass))+geom_density(alpha=.3)


#----3.1.4 数据清洗后训练集数据质量
#数据质量表（总表）
train_data_quality<- data_quality(train)
train_data_quality 
#数据质量表（数值型）
numeric_train<- train[,c("Age","Fare","SibSp","Parch")]
quality_numeric_train<-quality_numeric(numeric_train)
quality_numeric_train
length(train$Fare[which(train$Fare==0)])
#数据质量表（类别型）
factor_train<- train[,c("Survived","Pclass","Sex","Embarked")]
quality_factor_train<- quality_factor(factor_train)
quality_factor_train
table(train$Embarked,useNA = "always")





#----3.2测试集数据清洗----####

#----3.2.1查看原始数据质量

#数据质量表（总表）
test_data_quality<- data_quality(test)
test_data_quality 
#---由数据质量表可知，训练集共有418条记录，年龄字段存在20.57%的缺失值（86条）,可根据姓名字段进行均值(或者中位数，或者分布）填补,且Survived,Pclass,Sex,Sibsp,Parch,Embarked为分类型变量，其他数据完整

#数据质量表（数值型）
numeric_test<- test[,c("Age","Fare","SibSp","Parch")]
quality_numeric_test<-quality_numeric(numeric_test)
quality_numeric_test
length(test$Fare[which(test$Fare==0)])
##---Fare存在2笔零值，可能是异常值，1笔缺失，船票的票价和乘客等级有关，因此可根据Pclass信息来做均值填补
# library(rcompanion)
# plotNormalHistogram(numeric_train[,1])
# plotNormalHistogram(numeric_train[,2])

#数据质量表（因子型）
factor_test<- test[,c("Pclass","Sex","Embarked")]
quality_factor_test<- quality_factor(factor_test)
quality_factor_test
##---类别型变量数据完整

#----3.2.2数据类型转换(字符型变为因子型)
test<- data_transform(test)
ggplot(test,aes(x=Age,fill=Pclass))+geom_density(alpha=.3)

#----3.2.3异常值处理Fare
#Fare为0 的值根据仓位等级的中位数进行填补(此处只有一等舱存在2个为0)
a2<-tapply(test$Fare,test$Pclass,median)
test[which(test$Fare==0&test$Pclass==1),"Fare"]<- a2[[1]]
#Fare为缺失的1个值根据仓位等级的中位数进行填补(此处只有三等舱存在1个缺失，但测试集中无三等舱，因此用训练集的三等舱插补)
test[is.na(test$Fare),]#查看缺失数据
test$Fare[is.na(test$Fare)]<- a1[[3]]

#----3.2.4处理缺失值---Age根据称呼用中位数插补年龄
# library(stringr)
table_words <- table(unlist(strsplit(test$Name,"\\s+")))  #table是为了对词进行计数
sort(table_words [grep('\\.',names(table_words))],decreasing = TRUE) #将含有.的词（这些代表称呼）提取出来排序
tb <- cbind(test$Age,str_match(test$Name,"[a-zA-Z]+\\.")) #（+代表一个或多个）
table(tb[is.na(tb[,1]),2])
median.mr <- median(test$Age[grepl("Mr\\.",test$Name)],na.rm = T) #方法一grepl返回布尔值，grep返回行号
median.mrs <- median(test$Age[grepl("Mrs\\.",test$Name)],na.rm = T) #方法二:加上na.rm=
median.dr <- median(test$Age[grepl("Dr\\.",test$Name)],na.rm = T)
median.miss <- median(test$Age[grepl("Miss\\.",test$Name)],na.rm = T)
median.master <- median(test$Age[grepl("Master\\.",test$Name)],na.rm = T)
cbind(median.mr,median.mrs,median.dr,median.miss,median.master)
#中位数填补
test$Age[grepl("Mr\\.",test$Name) & is.na(test$Age)] <- median.mr
test$Age[grepl("Mrs\\.",test$Name) & is.na(test$Age)] <- median.mrs
test$Age[grepl("Dr\\.",test$Name) & is.na(test$Age)] <- median.dr
test$Age[grepl("Miss\\.",test$Name) & is.na(test$Age)] <- median.miss
test$Age[grepl("Master\\.",test$Name) & is.na(test$Age)] <- median.master
#处理后缺失值可视化
missmap(test,main = "Missing Map")
aggr(test,numbers = TRUE)
#年龄仍然存在1个缺失值，查看详情并处理,名字里显示MS,女性，猜测是Mrs,用Mrs值填补
test[is.na(test$Age),]
test$Age[is.na(test$Age)]<-median.mrs
ggplot(test,aes(x=Age,fill=Pclass))+geom_density(alpha=.3)

#----3.2.5数据清洗后测试集数据质量
#数据质量表（总表）
test_data_quality<- data_quality(test)
test_data_quality 
#数据质量表（数值型）
numeric_test<- test[,c("Age","Fare","SibSp","Parch")]
quality_numeric_test<-quality_numeric(numeric_test)
quality_numeric_test
length(test$Fare[which(test$Fare==0)])
# library(rcompanion)
# plotNormalHistogram(numeric_train[,1])
# plotNormalHistogram(numeric_train[,2])
#数据质量表（因子型）
factor_test<- test[,c("Pclass","Sex","Embarked")]
quality_factor_test<- quality_factor(factor_test)
quality_factor_test

#----3.2.6文件写出
setwd("D:\\桃子的数据\\Titani Machine Learning from Disaster\\cleand_data")
write.csv(train,file = "train_clean.csv")
write.csv(test,file = "test_clean.csv")


#----3.3 筛选建模属性----####
#进行建模的属性筛选，因此乘客ID，姓名，票号，座位号，对模型拟合没有意义，此处进行剔除
# 最终参与建模的数据质量表如下。
names(train)
train.all<- train[,c(-1,-4,-9,-11)]
str(train)
names(test)
test.all<- test[,c(-1,-3,-8,-10)]
str(test)
#数据质量表
#数据质量表（总表）
train_data_quality<- data_quality(train.all)
train_data_quality 
#数据质量表（数值型）
numeric_train<- train.all[,c("Age","Fare","SibSp","Parch")]
quality_numeric_train<-quality_numeric(numeric_train)
quality_numeric_train
#数据质量表（类别型）
factor_train<- train.all[,c("Survived","Pclass","Sex","Embarked")]
quality_factor_train<- quality_factor(factor_train)
quality_factor_train

#----3.4 进行数据抽样----####
#数据抽样
set.seed(102)
select<- sample(1:nrow(train.all),nrow(train.all)*0.7)
train<- train.all[select,]
test<- train.all[-select,-1]
test.y<-train.all[-select,1]

#--------第四部分：建立模型--------####

#----4.1逻辑回归----####
# 说明1：glm函数会自动将预测变量中的分类变量编码为虚拟变量
# 说明2：指定参数type="response"即可得到预测为1的概率
fit.logit<- glm(Survived~.,data = train,family = binomial())
summary(fit.logit)
prob<- predict(fit.logit,test,type="response")
pred.logit<-  factor(prob>0.5,levels = c(FALSE,TRUE),labels = c("0","1"))
pref.logit<-table(test.y,pred.logit,dnn=c("Actual","Predicted"))
pref.logit
# 结果：模型有参数未通过显著性检验，采用逐步回归
logit.fit.reduced<-step(fit.logit)
summary(logit.fit.reduced)
# 新模型为Survived ~ Pclass + Sex + Age + SibSp + Embarked
fit.logit<- glm(Survived ~ Pclass + Sex + Age + SibSp + Embarked,
                data = train,family = binomial())
# 结果：逐步回归后的模型效果不理想，因此仍然采取原来的模型


#----4.2决策树----####
# 说明1：用全部变量建树，根据复杂度参数cp进行剪枝
# 说明2：fit.tree$cptable 是十折交叉验证的复杂度参数及误差，从中选择预测误差最小的树
# 说明3：验证时，加上type="class"输出分类结果，否则输出概率值
library(rpart)
library(rpart.plot)
fit.tree<- rpart(Survived~.,data = train,method = "class",
                 parms = list(split="information"),control = rpart.control(xval = 10))
plotcp(fit.tree)
fit.tree$cptable  #复杂度参数 error树的误差 xerror十折交叉验证误差 xstd交叉验证标准差
prune.tree<- prune(fit.tree,cp=0.015) #剪枝

prp(prune.tree,type = 2,extra = 104,fallen.leaves = T,main="Decision Tree")#画出最终决策树 
# green if survived
cols <- ifelse(prune.tree$frame$yval == 1, "darkred", "green4")
prp(prune.tree, main="Decision Tree",
    extra=106,           # display prob of survival and percent of obs
    nn=TRUE,             # display the node numbers
    fallen.leaves=TRUE,  # put the leaves on the bottom of the page
    shadow.col="gray",   # shadows under the leaves
    branch.lty=3,        # draw branches using dotted lines
    branch=.5,           # change angle of branch lines
    faclen=0,            # faclen=0 to print full factor names
    trace=1,             # print the automatically calculated cex
    split.cex=1.2,       # make the split text larger than the node text
    split.prefix="is ",  # put "is " before split text
    split.suffix="?",    # put "?" after split text
    col=cols, border.col=cols,   # green if survived
    split.box.col="lightgray",   # lightgray split boxes (default is white)
    split.border.col="darkgray", # darkgray border on split boxes
    split.round=.5)              # round the split box corners a tad

rpart.plot(prune.tree,branch=1, extra=106, under=TRUE, faclen=0,
           cex=0.8, main="决策树")
pred.tree<- predict(prune.tree,test,type="class") #验证
pref.tree<-table(test.y,pred.tree,dnn=c("Actual","Predicted"))
pref.tree

#----4.3随机森林----####
# 说明1：随机森林默认生成500棵树，在每个节点处抽取sqrt(M)个变量
#说明2：importance(fit.ranf,type=2)查看变量重要性
# 说明3：na.action = na.roughfix参数将数值变量中的缺失值以对应列中位数替代，类别变量用众数。
# 说明3：randomForest生成传统决策树，而party包中的cforest()基于条件推断树生成随机森林
library(randomForest)
fit.ranf<- randomForest(Survived~.,data = train,na.action = na.roughfix,importance=T)
fit.ranf
importance(fit.ranf,type=2)

pred.ranf<- predict(fit.ranf,test)#验证
pref.ranf<-table(test.y,pred.ranf,dnn=c("Actual","Predicted"))
pref.ranf

#----4.4支持向量机----####
# 说明：SVM从本质上来讲是一个黑盒子，在对大量样本建模时不如随机森林，但只要建立了一个成功的模型，在对新样本分类时就没有问题了
# 说明1：ksvm{kernlab}功能强大 / svm{e1071}相对简单
# 说明2：由于方差大的预测变量对SVM生成影响更大，所以svm默认建模前对每个变量标准化
# 说明3：na.omit(validate) 与随机森林不同，SVM在预测新样本单元时不允许缺失值
library(e1071)
fit.svm<- svm(Survived~.,data = train)
fit.svm
pred.svm<- predict(fit.svm,na.omit(test))#验证
pref.svm<-table(na.omit(test.y),pred.svm,dnn=c("Actual","Predicted"))
pref.svm
#调和参数
# 说明1：svm默认通过径向基函数radial basis（RBF）将样本投射到高维空间
# 因此gamma(核函数参数，控制分割超平面形状)越大，支持向量越多,cost（犯错误成本）越大，可能导致过拟合
# 解决：用tune.svm对每个参数设置一个候选范围，搜索最优参数
# gamma(0.000001-10),cost(0.01,1010) 组合8*21 一共168个模型
# tuned<- tune.svm(Survived~.,data = train,gamma = 10^(-6:1),cost = 10^(-10:10))
# tuned
# # 将mamma=0.01 cost=1代回原模型
# fit.svm<- svm(class~.,data = train,gamma=0.01,cost=1)


# ---4.5 用boosting提升算法来生成组合模型-----#####
library(adabag)
#1.1--单一训练集建模
ada<- boosting(Survived~.,data = train)
pre<-predict(ada,test)
# pre$class 预测结果
# pre$confusion #混淆矩阵
pref.ada<-table(test.y,pre$class,dnn=c("Actual","Predicted"))
pref.ada




#--------第五部分：模型评估及选择--------####
# 利用混淆矩阵得到5种模型的精确度，如下表：
per.logit<- performance(pref.logit)
per.tree<- performance(pref.tree)
per.ranf<- performance(pref.ranf)
per.svm<-performance(pref.svm)
per.ada<- performance(pref.ada)
evaluating<- as.data.frame(cbind(per.logit,per.tree,per.ranf,per.svm,per.ada))
names(evaluating)<- c("Logit","tree","RandomForst","SVM","Adaboost")
evaluating
#SVM支持向量机的准确率为84%，采用SVM进行预测

#--------第六部分：生存预测--------####

#---结论，决策树预测准确率更高
# sensitivity=0.96
# specificity=0.95
# positivive predictive value=0.91
# negtive predictive value=0.98
# accuracy=0.952
# F1=0.94
#---结论，SVM预测准确率更高,
#  performance(pref.svm)
# sensitivity=0.69
# specificity=0.93
# positivive predictive value=0.85
# negtive predictive value=0.83
# accuracy=0.84
# F1=0.76
head(test.all)
prediction.svm<- predict(fit.svm,na.omit(test.all))  #预测

#写出结果
prediction<- as.data.frame(prediction.svm)
names(prediction)<- c("Survival")
write.csv(prediction,file = "prediction2.csv")
# prediction_n<-read.csv("prediction.csv",header = T,sep = ",")
# d<-cbind(prediction_n,prediction)
# d[!d$Survived==d$Survival,]