Graph Embedding（SDNE，Graph2vec）

SDNE
前一篇整理了3种常用的图嵌入方法，DeepWalk，LINE和Node2vec。Structural Deep Network Embeddings（结构深层网络嵌入，SDNE）的不同之处在于，它并不是基于随机游走的思想，在实践中比较稳定。

主要思路如上图，会将节点向量 si 作为模型的输入，通过自编码器对这个向量进行降维压缩 zi，然后再重建特征。其损失函数定义为：
$$O_2=\sum ||s_i^{\prime }-s_i|{|}_2^2$$

因为输入的是邻接矩阵，所以这样的重构能够使得结构相似的顶点具有相似的embedding表示向量。所以实际上通过重建学习到的是二阶相似度。

但是与LINE相似，SDNE也想保留一阶和二阶相似度，而且是想要同时优化，以同时捕获局部成对相似性和节点邻域结构的相似性。对于一阶相似度的计算，将架构变成如上图，由左右两个自编码器组成。一阶相似度的目标是计算节点间的相似性，那么可以利用起中间的嵌入得到的隐层向量z，然后计算左侧嵌入和右侧嵌z入间的距离。并可以用拉普拉斯矩阵优化一下计算：
$$O_1=\sum ||z_1-z_2|{|}_2^2==2tr(Z^{T}LZ)$$

再加上正则项reg，总损失为：$$L=O_2+\alpha O_1+v{O}_{reg}$$论文出自KDD 2016的《Structural Deep network Embedding》，作者的完整代码code开源：https://github.com/suanrong/SDNE

def __make_loss(self, config):
        def get_1st_loss_link_sample(self, Y1, Y2):
            return tf.reduce_sum(tf.pow(Y1 - Y2, 2))
        def get_1st_loss(H, adj_mini_batch):
            D = tf.diag(tf.reduce_sum(adj_mini_batch,1))
            L = D - adj_mini_batch ## 拉普拉斯矩阵
            return 2*tf.trace(tf.matmul(tf.matmul(tf.transpose(H),L),H))

        def get_2nd_loss(X, newX, beta):
            B = X * (beta - 1) + 1
            return tf.reduce_sum(tf.pow((newX - X)* B, 2))
		#对w和b的正则化项
        def get_reg_loss(weight, biases):
            ret = tf.add_n([tf.nn.l2_loss(w) for w in weight.itervalues()])
            ret = ret + tf.add_n([tf.nn.l2_loss(b) for b in biases.itervalues()])
            return ret
            
        #总损失函数
        self.loss_2nd = get_2nd_loss(self.X, self.X_reconstruct, config.beta)
        self.loss_1st = get_1st_loss(self.H, self.adjacent_matriX)
        self.loss_xxx = tf.reduce_sum(tf.pow(self.X_reconstruct,2)) 
        self.loss_reg = get_reg_loss(self.W, self.b) 
        return config.gamma * self.loss_1st + config.alpha * self.loss_2nd + config.reg * self.loss_reg

其实似乎这个建模的思路和矩阵分解是差不多的，只是在降维时用的不是矩阵分解，而是自编码器，并融入了一阶与二阶的概念。

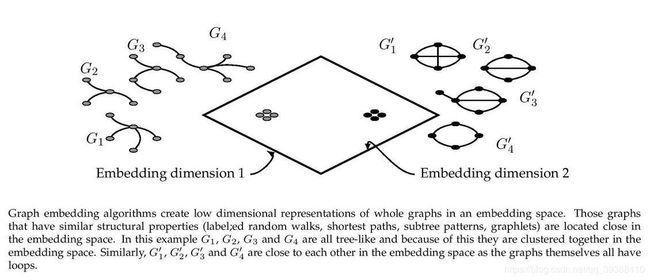
Graph2vec
出自MLGWorkshop 2017的《graph2vec: Learning Distributed Representations of Graphs》
直接对整个图进行嵌入。原理上和DeepWalk差不多，也是尝试借用word2vec来训练，只是这次为了嵌入整张图，所以尝试利用子图来训练。类似文档嵌入doc2vec，通过最大化作为输入的文档，来预测随机单词的可能性，Graph2vec预测图中子图的概率。

• 采样子图。为了提高效率，采样只选当前节点周围的邻接节点，构成子图sg。
• skip-gram。最大化输入图子图的概率$J(\Phi )=-logP(s{g}_n^{(d)}|\Phi (G))$，d为度，sg为子图。
  

#把图处理成doc2vec问题的形式就可以用gensim了
from gensim.models.doc2vec import Doc2Vec, TaggedDocument

#得到Wisfeiler-Lehman特征
def do_a_recursion(self):
        new_features = {}
        for node in self.nodes:
            nebs = self.graph.neighbors(node)
            degs = [self.features[neb] for neb in nebs]
            features = [str(self.features[node])]+sorted([str(deg) for deg in degs])
            features = "_".join(features)
            hash_object = hashlib.md5(features.encode())
            hashing = hash_object.hexdigest()
            new_features[node] = hashing
        self.extracted_features = self.extracted_features + list(new_features.values())
        return new_features

作者开源：https://github.com/benedekrozemberczki/graph2vec

Graph Neural Network
图神经网络(Graph Neural Network, GNN)也是很好的图嵌入方法。GNN包括图卷积神经网络（GCN），图注意力网络（GAT），Graph LSTM等等，虽然技术上还是和CV，NLP领域内的方法很像。。。

图表征学习的局限

• 参数量大，每个顶点都有唯一的标准向量
• 不能给未出现的顶点生成表征向量
• 部分图表征学习不能融合属性特征等信息

最后献上很全很全的论文集：https://github.com/benedekrozemberczki/awesome-graph-classification