图神经网络用于推荐系统问题(PinSage,EGES,SR-GNN)
针对推荐系统的稀疏性问题,图方法还真的很适合。PinSage和EGES都是很好的落地实践方法,首先来看一下对于user-item二部图的一般处理方法:

GCMC - Graph Convolutional Matrix Completion
发表在KDD2018,将user-item矩阵补全问题抽象成了二分图的连接预测问题。每种连接预测的边可以视为lable(如点击,购买,收藏等等,1-5的评分也可以),然后用二部图的方法来进行链接预测(即预测是否点击或者预测评分是多少,就变成了分类预测问题)。
虽然也可以图特征提取模型和链接预测模型,不管本文具体方式上如上图,是使用图自编码器进行端到端建模。
- Graph convolutional encoder。即使用节点消息传递来更新模型参数,比如从item j 到 user i: μ j → i , r = 1 c i j W r x j v μ_{j→i,r} = \frac{1}{c_{ij}}W_r x_ j^v μj→i,r=cij1Wrxjv其中c是正则化,W是控制变类型的权重,x是j的特征。从user到item当然也是同样的方法,然后对每个节点都进行这样的消息传递,最后就能得到每个节点的表示(如user的表示是用一个权重W对其所有相邻节点的表示聚合得到)。
- Bilinear decoder 。重建链路,即把每个不同的评分等级(或者点击,购买等)看作是一类 P = e ( z i u ) T Q r z j v ∑ s = 1 R e ( z i u ) T Q r z j v P=\frac{e^{(z_i^u)^TQ_r z_j^v}}{\sum_{s=1} ^R e^{(z_i^u)^TQ_r z_j^v}} P=∑s=1Re(ziu)TQrzjve(ziu)TQrzjv其中 z i u , z j v z_i^u,z_j^v ziu,zjv是用户,商品的表示,Q是转化矩阵,最后计算一个softma分数来预测“分类”就可以了。
GCMC使用消息传递+自编码的思想,实际上在大图应用中对每个节点做消息传递太过复杂。在实践应用中还是使用随机游走+其他,接下主要介绍PinSage,EGES。

Graph Convolutional Neural Networks for Web-Scale Recommender Systems
PinSage,一个能够学习节点嵌入的随机游走GCN,由Pinterest公司和Stanford完成的工作,首次将图方法落地到了工业界。PinSage的理论背景是基于GraphSAGE,即归纳(inductive)式的学习,直接学习聚合函数而不是固定的节点,这也是其他的图算法如GCN等等直推式(transductive)方法无法做到的,更能满足实际中的图节点是不断变化的需求(节点和关系都会不断的变化)。
首先看看需求。Pinterest公司是世界上最大的图片社交分享网站,业务采用瀑布流的形式向用户展现图片(抖音也很像这种模式),并且允许用户创建和管理主题图片集合。网站上的大量图片称为pins,而用户喜欢的图片集合(类似收藏夹),即称为pins钉在画板 的pinboards上。于是pins和boards就形成了如开头图片所示的二部图形式。
挖掘这种二部图的目的在哪里?
分析用户兴趣,帮助用户发现和匹配他们感兴趣的图片(商品)。虽然Pinterest的数据显然都是一堆图片,但是图片节点本身的信息是无法通过CNN-based方法来解决的。如图像识别,床栏和花园栅栏都是条状的“栏”,被分为一类的概率很大,这并不能提供很多有用的信息,但是如果看看这两个图片在Graph中的位置就会发现区别很大,因为大门和花园栅栏通常会成为邻居节点,但是床和大门却很少相邻。这也就是图的优点,可以通过邻居节点的信息,位置得到更丰富的嵌入特征。
- 模型的输入Graph是数十亿对象的web-scale graph(30亿个节点,180亿),节点是图片(需要注意的是,节点特征包括视觉特征和文本特征)。然后可以将图分成Pin和Pinboard(实际上可以看作是pin的上下文信息),依照关系可以构建二部图。
PinSage
PinSage基于GraphSAGE,GraphSAGE博主以前已经整理过了,所以不做过多的展开。简单来说它的核心思想就是学习聚合节点的邻居特征生成当前节点的信息的聚合函数,有了聚合函数不管图如何变化,都可以通过当前已知各个节点的特征和邻居关系,得到节点的embedding特征。
GraphSage(Graph SAmple and aggreGatE),很重要的两步就是Sample采样和Aggregate聚合,PinSage也是一样。
首先是Convolve部分,这部分相当于GraphSage算法的聚合阶段过程,伪代码如下:

输入是当下节点u的嵌入 z u z_u zu,然后得到它的邻居节点 z e z_e ze,然后主要对应伪码的1,2,3步:
- 聚合邻居。可以看到,所有的邻居节点特征 h z h_z hz都经过一层dense层(由Q和q参数控制,再ReLU激活),再由聚合器或池化函数 γ \gamma γ (如mean等)将所有邻居节点的信息聚合得到 n u n_u nu
- 更新当前节点的特征。将原特征 z u z_u zu和 n u n_u nu拼接后再经过一层dense层(W,w参数控制,再ReLU激活)
- 最后归一化。直接对上一步得到的特征归一化
所以其实Convolve和GraphSage的不同之处就在于聚合邻居特征前多做了一步dense层抽象特征。
然后是minibatch对应着采样邻居部分,伪代码如下:

采样方法实际上就是在某个Minibatch内,以所有节点作为起始节点,然后做一个bfs去获取一定数量的邻居节点(步长固定为K的路径),最后按照逐层方式进行多层的卷积。
- 2~7行是邻居采样阶段。不沿用GraphSage的随机采样,而是使用访问数作为重要性采样。即每次从当前节点出发随机走,虽然一开始是平均的,游走很多次之后,被走到的次数越多的节点,它相对于当前节点的重要性就越高,最终选取top-t的邻居。
- 然后后面就是Convolve操作了逐层的生成节点嵌入特征。特别注意就是要经过dense之后才更新特征(伪码15-16)。
训练损失使用的是常规负采样之后,再使用的max-margin ranking loss,即最大化正例之间的相似性,同时保证与负例之间相似性小于正例间的相似性: J G ( z q , z i ) = E n k ∼ P n ( q ) m a x { 0 , z q ⋅ z n k − z q ⋅ z i + △ } J_G(z_q,z_i)=E_{n_k \sim P_n(q)} max\{0,z_q \cdot z_{n_k}-z_q\cdot z_i +\triangle\} JG(zq,zi)=Enk∼Pn(q)max{0,zq⋅znk−zq⋅zi+△}
训练技巧:
- 简单负采样会导致模型分辨的粒度过粗,没针对性,特别是数据量如此大的情况下。所以增加了“hard”负样本,即根据当前节点相关的PageRank排名,选排名在2000-5000之间的items为“hard”负样本候选集,再进行随机采样,以增加训练难度。
- Multi-GPU形式,minibatch取值为512-4096不等,大的batchsize可能会导致收敛困难。所以使用warmup:在第一个epoch中将学习率线性提升到最高,后面的epoch中再逐步指数下降。
- Minibatch里具有较多样本,一个GPU无法计算。所以将这个Minibatch的图切成很多个子图,每个子图在一个GPU上,来做GPU并行的求梯度,最后再将梯度汇集起来更新参数。
- 为了大规模计算设定的两个MapReduce任务:1)执行聚合所有pins的嵌入特征 2)执行采样邻居特征得到board的嵌入特征。
Billion-scale Commodity Embedding for E-commerce Recommendation in Alibaba
同样的阿里其实也基于GraphSAGE做过相关工作(或许GraphSAGE在工业落地上是最有优势的了),发自KDD 2018。为了解决在推荐系统中的老三样困难:可扩展性,稀疏性和冷启动。所以提出了:
- 可以根据用户的历史行为来构建商品图(如上图的a和b,根据用户的一些点击记录,依照连续点击应该存在关系,可以构造出如b一样的item graph),并学习图中所有商品的嵌入(如图c的带权随机游走采样,用deepwalk思想基于skip-gram训练embedding)。这一步就是作者描述的Base Graph Embedding(BGE)。
- 为了减轻稀疏性和冷启动问题,将边信息合并到图嵌入框架中。即增加商品的属性,如品牌,价格等。然后就升级成了Graph Embedding with Side information (GES),并且对不同的side Information加权得到Enhanced Graph Embedding with Side information (EGES)。
插一句这个历史行为构图其实就是session-based会话推荐了,这个下一篇文章会继续详细介绍。EGES模型图如下:
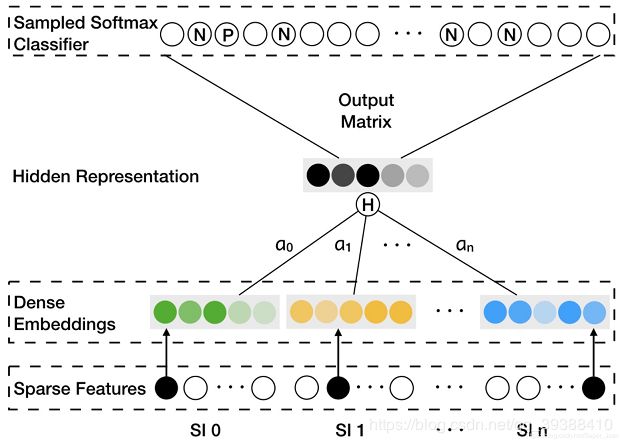
看图可知,就是把特征one-hot之后Embedding,再用注意力算一次权重H之后concat所以的特征,最后一层dense就得到了商品的特征。EGES只是把side Information带权加入进来,即把每个item的特征变丰富了。之后还是用deepwalk思想采样变“句子”,基于skip-gram训练embedding,DeepWalk博主整理过了就不说了吧,最后也是一个负采样训练的常规操作。

Session-based Recommendation with Graph Neural Networks
会话序列推荐的图应用,发自AAAI 2019,先放链接:
blog:https://sxkdz.github.io/research/SR-GNN/
paper:https://arxiv.org/abs/1811.00855
code:https://github.com/CRIPAC-DIG/SR-GNN
这篇文章和上一篇很像,只是不是用DeepWalk,而是GNN的。首先,会话推荐是指,对于一个用户的点击序列(即session),预测下一个要点击的物品。即输入所有的物品V={v1,v2,…,vm} ,在给定某个session为s=[v1,v2,…,vn]的用户点击序列,预测下一个要点击的物品vn+1。
现有基于会话的推荐,方法主要集中于循环神经网络和马尔可夫链,但是存在以下缺陷:
- 当一个session中用户的行为数量十分有限时,RNN很难产生好的用户特征
- 马尔可夫链非常依赖数据独立性的假设
- 同时,物品之间的转移模式在会话推荐中是十分重要,但RNN和马尔可夫过程只对相邻的两个物品的单向转移关系进行建模,而忽略了会话中其他的物品(即上下文)。
所以不如直接将会话序列建模为图结构数据,并使用图神经网络捕获复杂的项目物品item间转换,每一个会话利用注意力机制将整体偏好与当前偏好结合进行表示。同时这种方式也就不依赖用户的表示了,完全只基于会话内部的潜在向量获得Embedding,然后预测下一个点击。
Graph Neural Networks
对于构图的表示,可以看模型图的最左边红色部分,对于一连串的点击序列,就直接利用点击关系构图就ok。然后抽取这个会话图中的每个物品的Embedding向量,利用物品的Embedding向量再进行预测。
抽取序列中物品特征的GNN部分使用 Gated GNN,其计算公式为:

H和b是权重矩阵和偏置,v是点击物品序列。 A s A_s As是由两个邻接矩阵,即入度和出度A(in)和A(out)矩阵拼接而成的(n, 2n)的矩阵,而 A s , i A_{s,i} As,i可以理解成矩阵的第i行(1, 2n)。如下图所示:

A s , 2 A_{s,2} As,2代表的就是红色的那一行,这样做的目的是使模型能结合出度入度以学习到更复杂的图上下文关系。至此GNN的部分实际上就结束了…后面的四个公式就是普通的RNN了,即利用某点在图中的特征表示再RNN。
Attention策略
得到item的特征向量后(模型图中的彩色条),应用一个注意力机制。有一点不同的是作者认为在当前的会话序列中,最后一个物品是非常重要的,所以单独将它作为 s 1 s_1 s1,然后计算其他的物品与最后一个物品之间的相关性,再加权就得到了 s g s_g sg以考虑到全局信息:
α i = q T σ ( W 1 v n + W 2 v i + c ) \alpha_i=q^T \sigma(W_1v_n+W_2v_i+c) αi=qTσ(W1vn+W2vi+c) s g = ∑ i = 1 n α i v i s_g=\sum_{i=1}^n \alpha_iv_i sg=i=1∑nαivi
接着将得到的 s 1 s_1 s1和 s g s_g sg连接,输入到一个线性层
s h = W 3 [ s 1 ; s g ] s_h=W_3[s_1;s_g] sh=W3[s1;sg]
最后使用 s h s_h sh和每个物品的embedding进行内积计算,再softmax得到最终每个物品的点击率,最后交叉熵得到损失函数:
L ( y ′ ) = − ∑ i = 1 m ( y i l o g p ( y i ′ ) + ( 1 − y i ′ ) l o g ( 1 − p ( x ) ) ) L(y')=-\sum_{i=1}^m(y_ilogp(y'_i)+(1-y'_i)log(1-p(x))) L(y′)=−i=1∑m(yilogp(yi′)+(1−yi′)log(1−p(x)))
总结
当然只要有关系的地方就能构图,就能抽图特征,特别是最近Graph这么火…万物皆可Graph。比如有人的地方就能有社交关系等等,最近有很多论文是针对属性中的异构信息进行挖掘,下一篇博文再整理。