Spectral Clustering(谱聚类)
谱聚类原理:
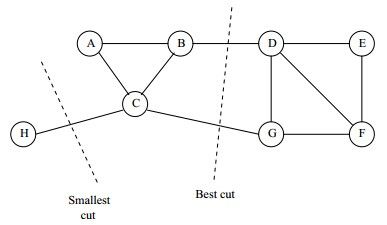
是一种基于图论的聚类方法!!简而言之,它将带权无向图划分为两个或两个以上的最优子图,使子图内部相似,而子图间相异,依然是很正统的聚类思想。但这个思想乍看很简单,主要有两个问题:怎么度量相似?度量之后又如何进行划分?
相似度度量:
普通的kNN度量方法?相近则权重大,相远则权重小。不过在实际应用中往往采用的全链接方法,即利用高斯分布来进行权重的赋予。
划分策略:
一个直观的想法就是,使划分成的子图内部相似度最大,子图之间的相似度最小。那么自然可以得到划分的损失函数: c u t ( A 1 , A 2 , . . . A k ) = 1 2 ∑ i = 1 k W ( A i , A ‾ i ) , 其 中 W 是 相 似 度 权 重 矩 阵 cut(A_1,A_2,...A_k) = \frac{1}{2}\sum\limits_{i=1}^{k}W(A_i, \overline{A}_i ),其中W是相似度权重矩阵 cut(A1,A2,...Ak)=21i=1∑kW(Ai,Ai),其中W是相似度权重矩阵
A ‾ \overline{A} A是A的补集。那么直接使这个函数值最小即可。但这种方法需要对每个子图的规模做出限定,需要遍历所有的可能切分进行相似度计算,于是RatioCut,Ncut等优化切分方法就出现了。
1.RatioCut:最小化损失函数的同时,最大化每个子图的个图总数,考虑划分平衡。于是划分为两个子图的损失函数就变为: R a t i o C u t ( A 1 , A 2 , . . . A k ) = 1 2 ∑ i = 1 k W ( A i , A ‾ i ) ∣ A i ∣ RatioCut(A_1,A_2,...A_k) = \frac{1}{2}\sum\limits_{i=1}^{k}\frac{W(A_i, \overline{A}_i )}{|A_i|} RatioCut(A1,A2,...Ak)=21i=1∑k∣Ai∣W(Ai,Ai)
那么如何最小化这个式子?图论中有一个拉普拉斯定理(这在图卷积任务上会有很重要的作用): f T L f = f T D f − f T W f = 1 2 ∑ i , j = 1 n w i j ( f i − f j ) 2 , 其 中 D 是 点 的 度 矩 阵 f^TLf = f^TDf - f^TWf = \frac{1}{2}\sum\limits_{i,j=1}^{n}w_{ij}(f_i-f_j)^2,其中D是点的度矩阵 fTLf=fTDf−fTWf=21i,j=1∑nwij(fi−fj)2,其中D是点的度矩阵
由此我们可以令 h j = 1 ∣ A j ∣ 作 为 一 个 指 示 向 量 h_{j}= \frac{1}{\sqrt{|A_j|}}作为一个指示向量 hj=∣Aj∣1作为一个指示向量,然后进行化简得到:
R a t i o C u t ( A 1 , A 2 , . . . A k ) = 1 2 ∑ i = 1 k W ( A i , A ‾ i ) ∣ A i ∣ = ∑ i = 1 k h i T L h i = ∑ i = 1 k ( H T L H ) i i RatioCut(A_1,A_2,...A_k) = \frac{1}{2}\sum\limits_{i=1}^{k}\frac{W(A_i, \overline{A}_i )}{|A_i|} = \sum\limits_{i=1}^{k}h_i^TLh_i = \sum\limits_{i=1}^{k}(H^TLH)_{ii} RatioCut(A1,A2,...Ak)=21i=1∑k∣Ai∣W(Ai,Ai)=i=1∑khiTLhi=i=1∑k(HTLH)ii
然后怎么继续化简呢?由线性代数我们可以知道,若 L H = λ H LH=\lambda H LH=λH,即 λ \lambda λ为它的特征值,然后对该式两边左乘一个 H T H^T HT,可得 H T L H = λ H T H H^TLH=\lambda H^TH HTLH=λHTH,而 H T H = I H^TH=I HTH=I,故该式就是矩阵的特征值之和–迹了。
R a t i o C u t ( A 1 , A 2 , . . . A k ) = t r ( H T L H ) RatioCut(A_1,A_2,...A_k) = tr(H^TLH) RatioCut(A1,A2,...Ak)=tr(HTLH)
哇,然后再次感觉似乎很简单了,最小化cut等于最小化这个迹就行。但是同样的最小化这个矩阵的迹也很困难,还是需要对所有的点的进行划不划分的判断,即 2 n 2^n 2n种可能性。所以我们只能退而求其次,找到最小的k个矩阵特征值进行拟合逼近,这样就最小化了这个式子。但是这样做的后果是丢失了一些信息,结果可能会有偏差,所以最后还需要使用K-Means聚类之类的聚类方法对少数的特征进行聚类。
所以谱聚类的算法就变成了算各种矩阵之后,选出最小的k个特征向量,一般需要做个标准化后变成一个特征矩阵,再对这个矩阵进行一次简单的聚类就ok了。(在GCN中由于k个特征值很难计算,所以又进行了傅里叶滤波和切比雪夫多阶逼近的方法。)
什么是谱?
矩阵特征值。
2.Ncut:单凭数量没什么说服力,该点的重要程度,其连通性复杂性应该被重视。所以用点的度矩阵也许效果更好。此时损失函数变为: N C u t ( A 1 , A 2 , . . . A k ) = 1 2 ∑ i = 1 k W ( A i , A ‾ i ) v o l ( A i ) , 其 中 v o l ( A i ) 是 度 矩 阵 NCut(A_1,A_2,...A_k) = \frac{1}{2}\sum\limits_{i=1}^{k}\frac{W(A_i, \overline{A}_i )}{vol(A_i)},其中vol(A_i)是度矩阵 NCut(A1,A2,...Ak)=21i=1∑kvol(Ai)W(Ai,Ai),其中vol(Ai)是度矩阵
求解方法与思路基本没什么区别,只是L变成 了 D − 1 / 2 L D − 1 / 2 了D^{-1/2}LD^{-1/2} 了D−1/2LD−1/2(又称归一化)而已,计算速度上会稍稍的快一点。
SC应用:
SpectralClustering参数说明:
SpectralClustering(affinity=‘nearest_neighbors’, assign_labels=‘kmeans’,coef0=1, degree=3, eigen_solver=‘arpack’, eigen_tol=0.0,gamma=1.0, kernel_params=None, n_clusters=2, n_init=10, n_jobs=1,n_neighbors=10, random_state=None)
affinity='nearest_neighbors',:相似度度量方式
assign_labels='kmeans':最后聚类方式的选择
coef0=1:核函数,对应affinity的某些需要
degree=3:核函数,对应affinity的某些需要
eigen_solver='arpack':降维时的工具
eigen_tol=0.0:停止条件
gamma=1.0,:核函数,对应affinity的某些需要
kernel_params=None:自定义核函数
n_clusters=2:切分时的k个特征向量
n_init=10:赋不同初值的次数阈值
n_neighbors=10:affinity中的k
利用sklearn做谱聚类:
基本代码很简单就不贴了,可以参照之前其他篇章内的代码稍作修改即可。仅贴出数据集。
#数据点
X,noisy_circles = datasets.make_circles(n_samples=1500, factor=.5,
noise=.05)