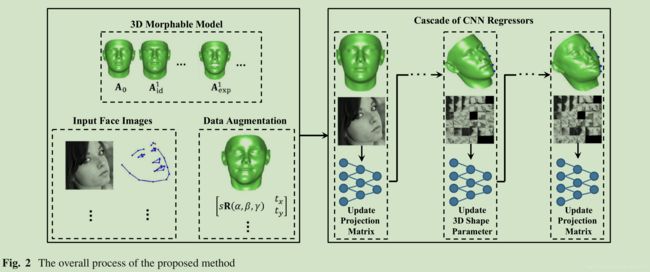
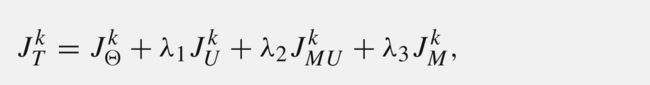人脸关键点对齐:Pose-Invariant Face Alignment via CNN-Based Dense 3D Model Fitting 论文解析
1.摘要部分
1.为什么要提出姿态不变的人脸对齐
姿态不变的人脸对齐在CV中占据着非常重要的地位,在脸部分析中人脸对齐是一个首要必备的条件。例如人脸重建,表情重建和3D人脸重建。
2.论文中提出的方法
在这篇Paper中,大神提出了使用3DMM匹配算法并用C-CNN回归相机投影矩阵参数(m),以及3DMM的shape参数(p)以及提供了镜像约束作为loss函数。
2. Introduction部分
这部分就简单的写写了,大家可以自己认真的阅读一下!
这里面介绍了ASM,AAM和级联回归方法的2D关键点对齐的方法
参考.
ASM,AAM
AAM,CLM
级联回归
级联回归的方法始于 P Dollar大神在CVPR2010的论文Cascaded pose regression,通过级联回归的方法来预测物体的形状。
对于人脸特征点定位,人脸关键点检测的目的是估计向量(Facial Shape) ,其中K表示关键点的个数,由于每个关键点有横纵两个坐标,所以S的长度为2K。 对于一个输入 I , 给定一个初始形状 (通常是在训练集计算得到的平均形状)。每一级输出的是根据输入图像得到的偏移估计 ,那么每一级都会更准确的预测脸上 Landmark 的位置

其中,S^t 和 S^{t+1} 分别表示第 和 级预测的人脸形状(即所有关键点集合),表示回归函数。
在级联形状回归的框架下,主要的操作是向量相加,不仅有效而且计算复杂度较低, 所以近年来得到了广泛的应用,并产生了很多改进算法, 其主要不同点在于特征提取方法以及回归函数的选择不同。值得一提的是,级联回归对与正脸或接近正脸的定位精度相对较高,而对于大姿态下的关键点定位效果相对较差。
引用链接:https://www.jianshu.com/p/e4b9317a817f
3DMM
这里还提到一些3DMM的知识
参考:
3DMM
作者的贡献
We summarize the main contributions of this work as:
• Pose-invariant face alignment by fitting a dense 3DMM,and integrating estimation of 3D shape and 2D facial landmarks from a single face image.
• The cascaded CNN-based 3D face model fitting algorithm that is applicable to all poses, with integrated landmark marching and contribution from local appearances around cheek landmarks during the fitting process.
• Dense 3D face-enabled pose-invariant local features and utilizing person-specific surface normals to estimate the visibility of landmarks.
• A novel CNN architecture with mirrorability constraint that minimizes the difference of face alignment results of a face image and its mirror.
简单的解释一下:
1.通过拟合一个稠密的3DMM模型,并从单个人脸图像中综合估计三维形状和二维人脸关键点,实现了位置不变的人脸对齐。
2.基于cnn的级联3DMM人脸模型拟合算法适用于所有的姿势,在拟合过程中集成了关键点跟踪和对局部脸颊的拟合过程中的贡献。
3.密集的三维人脸支持位置不变的局部特征,利用独特的人脸表面法线估计关键点的可见性
4.新颖的CNN架构以及镜像约束LOSS,将人脸图像和镜像比对结果的差异最小化。
3.3D face Alignment
(1)3D坐标和2D坐标的生成
这就是本文大神作者提出的方法的过程:
(1).首先给出2D图像通过3DMM的身份基( identity basis)和表情基( expression basis)并且通过下面的公式生成3D人脸 S = S 0 + ∑ i = 1 N i d P i d i S i d i + ∑ i = 1 N e x p P e x p i S e x p i S=S_0+\sum_{i=1}^{N_{id}}P_{id}^iS_{id}^i+\sum_{i=1}^{N_{exp}}P_{exp}^iS_{exp}^i S=S0+i=1∑NidPidiSidi+i=1∑NexpPexpiSexpi
where S is the 3D shape matrix, S 0 S_0 S0 is the mean shape, S i d i S_{id}^i Sidi is the i th identity basis, S e x p i S_{exp}^i Sexpi exp is the i th expression basis, P i d i P_{id}^i Pidi is the i th identity coefficient, and P e x p i P_{exp}^i Pexpi is the i th expression coefficient.
S = ( x 1 x 2 . . . x Q y 1 y 2 . . . y Q z 1 z 2 . . . z Q ) S= \left( \begin{array}{ccc} x_1 & x_2 & ...& x_Q\\ y_1 & y_2 & ...& y_Q\\ z_1 & z_2 & ...& z_Q \end{array} \right) S=⎝⎛x1y1z1x2y2z2.........xQyQzQ⎠⎞
这是3DMM算法拟合出来的3D形状矩阵,S再经过过投影为2D图像,3D的Q个点被投影为N个2D关键点,这些2D关键点组成矩阵U
U = ( u 1 u 2 . . . u N v 1 v 2 . . . v N ) U=\left( \begin{array}{ccc} u_1 & u_2 & ...& u_N\\ v_1 & v_2 & ...& v_N\\ \end{array}\right ) U=(u1v1u2v2......uNvN)
其中 U = s R S ( : , d ) + t U=sRS(:,d)+t U=sRS(:,d)+t
矩阵运算如下:
U=(2 ,N) 等于 s=a 乘以 R=(2, 3)乘以S(:,d)=(3, N)加t=(2, N)
where s is a scale parameter, R is the first two rows of a 3 × 3
rotation matrix controlled by three rotation angles α, β, and γ
(pitch, yaw, roll), t is a translation parameter composed of t x and
t y , d is a N-dim index vector indicating the indexes of
semantically meaningful 3D vertexes that correspond to 2D
landmarks.We form a projection vector m = (s,α,β,γ,t x ,t y ) ? which
collects all parameters to this projection.
s为缩放参数,R为旋转矩阵并且只要前两行,S为3D形状矩阵(:,d)表示取所有的行以及d中的所有的列,d是代表的与二维关键点对应的语义意义的三维顶点索引的集合,t是平移参数其中有 t x t_x tx和 t y t_y ty,m是进行投影的所有参数组成的
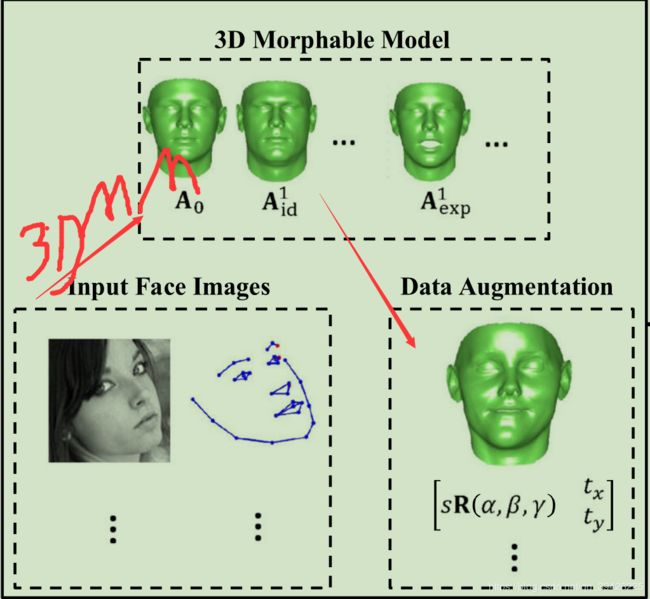
(2)Landmark marching
这个坐标跟踪就是更新脸颊的8个landmark因为这8个landmark最容易受rotation的影响。
Specifically, we define a set of paths each storing the indexes of vertexes that are not only the most closest ones to the original 3D cheek landmarks, but also on the contour of the 3D face as it turns. Given a non-frontal 3D face S, by ignoring the roll rotation γ, we rotate S by using the α and β angles (pitch and yaw), and search for a vertex in each predefined path that has the maximum (minimum) x coordinate, i.e., the boundary vertex on the right (left) cheek. These resulting vertexes will be the new 3D landmarks that correspond to the 2D cheek landmarks. We will then update relevant elements of d to make sure these vertexes are selected in the projection of Eq. 4. This landmark marching process is summarized in Algorithm 1 as a function d ← g(S,m). Note that when the face is approximately of profileview(|β| > 70 ◦ ),we do not apply landmark marching since the marched landmarks would overlap with the existing 2D landmarks on the middle of nose and mouth. Figure 3 shows the defined set of pathes on the 3D shape of face and one example of applying Algorithm 1 for updating vector d
*作者的意思是将旋转角度小于70度时如果原来的cheek landmark被遮挡时就找到新的cheek landmark坐标,大于70度时因为cheek landmark会于鼻子,眼睛和嘴巴的landmark重合所以放弃landmark marching,算法如下 —>


如上图所示将所有的path arg max,arg min 取x轴上最大,最小的8个坐标值更新为新的cheek landmark ,Update 8 elements of d with V c h e e k V_{cheek} Vcheek .
4.Data Augmentation
因为作者使用的数据集没有真实的m,p参数所以需要预测出最接近真实的m,p。
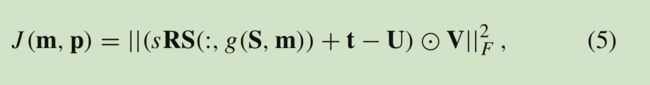
which is the difference between the projection of 3D landmarks and the 2D labeled landmarks. Note that although the landmark marching g(: , : ) makes cheek landmarks “visible” for non-profile views, the visibility V is still necessary to avoid invisible landmarks, such as outer eye corners and half of the face at the profile view, being part of the optimization.
V是一个是否可见的矩阵,可见为1,不可见为0 形如 U = ( 1 0 . . . 1 1 0 . . . 1 ) U=\left( \begin{array}{ccc} 1 & 0 & ...& 1\\ 1 & 0 & ...& 1\\ \end{array}\right ) U=(1100......11),最后相当于点乘V矩阵后再求行列式的平方,对于J(m,p)的优化就不赘述了。ps:(太难了,我也没看懂=-=)
5. Cascaded CNN Coupled-Regressor
For each training image I i , in addition to the ground truth m i m_i mi and p i p_i pi ,we also initialize image’s representation by, m 0 i = h ( m ¯ , b i ) m_0^i= h( m¯ ,b_i ) m0i=h(m¯,bi) and p 0 i p_0^i p0i= 0. Here ¯ m is the average of ground truth parameters of projection matrices in the training set, b i b_i bi is a 4-dim vector indicating the bounding box location, and h(m,b) is a function that modifies the scale and translations of m based on b。
where the true projection update is the difference between the current projection matrix parameter and the ground truth,i.e., Δ m k i = m i − m i k − 1 \Delta m_k^i=m_i-m_i^{k-1} Δmki=mi−mik−1, U i U_i Ui is current estimated 2D landmarks,computed via U = s R S ( : , d ) + t U=sRS(:,d)+t U=sRS(:,d)+t , based on m i k − 1 m_i^{k−1} mik−1 and d i k − 1 d_i^{k−1} dik−1, and v i k − 1 v_i^{ k−1} vik−1is estimated landmark visibility at stage k − 1
下面是CNN估计更新的投影矩阵参数如下:

形状p参数的更新于上部类似:

作者使用一个六级联的CNN,包括 C N N m 1 CNN_m^1 CNNm1, C N N m 2 CNN_m^2 CNNm2, C N N p 3 CNN_p^3 CNNp3, C N N m 4 CNN_m^4 CNNm4, C N N p 5 CNN_p^5 CNNp5, C N N m 6 CNN_m^6 CNNm6。在第一阶段, C N N m 1 CNN_m^1 CNNm1的输入层是由初始边界框裁剪的整个人脸区域,目的是粗略估计人脸的姿态。第二到第六阶段的输入是一个114×114的图像包含一组19×19 姿态不变的特征小方块,特征小方块是从当前预估的2D关键点得来的因为我们的 N = 34个关键点,最后两个特征小方块114×114的填满零。类似地,对于不可见的2D关键点也填满了零,形如下图------->。

6.Mirror Loss

这个镜像约束也就是老生常谈的把输入的图片镜像并且把镜像后的图片的原图片同时用CNN预测出shape参数的更新,再用他们的最小化他们的行列式值作为Loss进行优化
7.Mirror CNN Architecture
这里提到的孪生网络和权值共享参考 孪生网络 网络架构如下,很简单的

然后坐着又给出了一个总loss,很简单大家自己看一下就可以

In the bottom branch, we only have one loss (J MU ) for estimating the update of 2D shape in the mirror image. In total, we have four loss functions, one for the updates of morp,two for the 2D shape updates of two images respectively, and one mirror loss. We minimize the total loss at stage k
where λ 1 to λ 3 are weights for loss functions. Despite M-CNN appears more complicated to be trained than C-CNN,their testing are the same. That is, the only useful result at each cascade stage of M-CNN is the estimated update of the m or p, which is also passed to the next stage and initialize the input image features. In other words, the mirror images and estimated ?U in both images only serve as constraints in training, and are neither needed nor used in testing.
8. Visibility and 2D Appearance Features
这个就是基于每个人的身份基不一样得shape取法线判断是否可见

Specifically, given the Fig. 6 The person-specific 3D surface normal as the average of normals around a 3D landmark (black arrow). Notice the relatively noisy surface normal of the 3D “left eye corner”landmark (bluearrow) (Color figure online) current estimated 3D shape S, we compute the 3D surface normals for a set of sparse vertexes around the 3D landmark of interest, and the average of these 3D normals is denoted as N. Figure 6 illustrates the advantage of using the average 3D surface normal. Given N, we compute,
v = N T N_T NT · (R 1 × R 2 ), (15) where R 1 and R 2 are the first two rows of R.
接下来就是告诉我们如何取patch有两种方法PAWF和D3PF,具体看论文。PAWF还可以抗仿射变换提高CNN的识别不规范形状的能力,这个就好像和胶囊网络的抗仿射差不多。
9.总结
面部特征点定位问题(预测U)可以转变为同时预测投影矩阵m和3D人脸形状模型参数p
算法的整体框架通过级联6个卷积神经网络来完成这一任务:
(1) 首先以整张人脸图像作为输入,来预测投影矩阵的更新。
(2) 使用更新后的投影矩阵计算当前的2D人脸形状,基于当前的2D人脸形状抽取块特征作为下一级卷积神经网络的输入,下一级卷积神经网络用于更新3D人脸形状。
(3) 基于更新后的3D人脸形状,计算可得当前2D人脸形状的预测。
(4) 根据新的2D人脸形状预测,抽取块特征输入到卷积神经网络中来更新投影矩阵,交替迭代优化求解投影矩阵m和3D人脸形状模型参数p,直到在训练集收敛。
值得一提的是,该方法在预测3D人脸形状和投影矩阵的同时也考虑到计算每一个特征点是否可见。如果特征点不可见,则不使用该特征点上的块特征作为输入,这是普通2D人脸对齐方法难以实现的
此外,作者提出两种pose-invariant的特征Piecewise Affine-Warpped Feature (PAWF)和Direct 3D Projected Feature (D3PF),可以进一步提升特征点定位的精度。
原链接:https://www.jianshu.com/p/e4b9317a817f