【计算机视觉】详解 Non-local 模块与 Self-attention (视觉注意力机制 (一))

绪论

在计算机视觉中，注意力机制 (attention) 旨在让系统学会注意力 —— 能够忽略无关信息而关注重点信息。

近几年来，深度学习与视觉注意力机制结合的研究工作，大多数是集中于使用掩码 (mask) 来形成注意力机制。掩码的原理在于通过另一层新的权重，将图片数据中关键的特征标识出来，通过学习训练，让深度神经网络学到每一张新图片中需要关注的区域，也就形成了注意力。

注意力机制一种是软注意力 (soft attention)，另一种则是强注意力 (hard attention)。

• 软注意力的关键点在于，这种注意力更关注区域或通道，而且软注意力是确定性的注意力，学习完成后直接可以通过网络生成。最关键之处在于软注意力是可微的，可微的注意力就可通过神经网络算出梯度，并且前向传播和后向反馈来学习得到注意力的权重。

• 强注意力与软注意力不同点在于，首先强注意力是更加关注点，即图像中的每个点都有可能延伸出注意力，同时强注意力是一个随机的预测过程，更强调动态变化。当然，最关键之处在于，强注意力是一个不可微的注意力，训练过程往往是通过增强学习 (reinforcement learning) 来完成的。

许多计算机视觉领域的相关工作 (如分类、检测、分割、生成模型、视频处理等) 都在使用 soft attention，从而衍生出许多不同的 soft attention 用法。这些方法共同之处在于：利用相关特征学习权重分布，再将学习得到的权重施加于特征上，从而进一步提取相关知识。但施加权重的方式略有差别，可概括为：

• 加权可作用在原图上；

• 加权可作用在空间尺度上，给不同空间位置加权，如 PAM；

• 加权可作用在通道尺度上，给不同通道特征加权，如 CAM；

• 加权可作用在不同时刻历史特征上，结合循环结构添加权重，如机器翻译或视频相关的工作。

本文主要关注视觉应用中的 self-attention 机制及其应用 —— Non-local 网络模块。

---

一、视觉应用中的 self-attention 机制

1.1 self-attention 机制

由于卷积核作用的感受野是局部的，须累积经过许多层后才能将整个图像不同部分的区域关联起来。所以在 CVPR 2018 上出现了 SENet，从特征通道层面上统计图像的全局信息。以下将说明另一种特殊的 soft attention —— self attention。

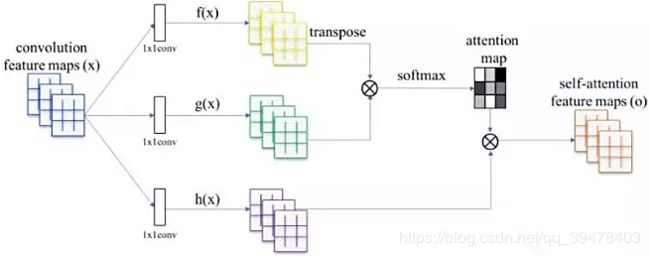
Self-attention 是借鉴自 NLP 的思想，因此仍保留了 Query，Key 和 Value 等名称。下图即为 self-attention 的基本结构，输入的 convolution feature maps 是由基本的主干 CNN (backbone) 提取的特征图，如 ResNet、Xception 等。通常将最后 ResNet 的两个下采样层去除，使得到的特征图尺寸为原输入图像的 1/8。

Self-attention 结构自上而下分为三个分支，分别是 query、key 和 value。计算时通常分为三步：

• 第一步，将 query 和每个 key 进行相似度计算得到权重，常用的相似度函数有点积、拼接、感知机等；

• 第二步，通常使用 softmax 归一化这些权重；

• 第三步，将归一化权重和 key 相应的 value 进行加权求和，得到最后的 attention。

接下来通过代码阐述 self-attention 原理：

class Self_Attn(nn.Module):
    """ Self attention Layer"""
    def __init__(self,in_dim,activation):
        super(Self_Attn,self).__init__()
        self.chanel_in = in_dim
        self.activation = activation
 
        self.query_conv = nn.Conv2d(in_channels = in_dim , out_channels = in_dim//8 , kernel_size= 1)
        self.key_conv = nn.Conv2d(in_channels = in_dim , out_channels = in_dim//8 , kernel_size= 1)
        self.value_conv = nn.Conv2d(in_channels = in_dim , out_channels = in_dim , kernel_size= 1)
        self.gamma = nn.Parameter(torch.zeros(1))
 
        self.softmax  = nn.Softmax(dim=-1)
    def forward(self,x):
        """
            inputs :
                x : input feature maps( B X C X W X H)
            returns :
                out : self attention value + input feature
                attention: B X N X N (N is Width*Height)
        """
        m_batchsize,C,width ,height = x.size()
        proj_query  = self.query_conv(x).view(m_batchsize,-1,width*height).permute(0,2,1) # B X CX(N)
        proj_key =  self.key_conv(x).view(m_batchsize,-1,width*height) # B X C x (*W*H)
        energy =  torch.bmm(proj_query,proj_key) # transpose check
        attention = self.softmax(energy) # BX (N) X (N)
        proj_value = self.value_conv(x).view(m_batchsize,-1,width*height) # B X C X N
 
        out = torch.bmm(proj_value,attention.permute(0,2,1) )
        out = out.view(m_batchsize,C,width,height)
 
        out = self.gamma*out + x
        return out,attention

假设输入 feature maps 的 shape = B×C×W×H  (Batch_size × Channels × Width × Height)

在初始化函数中定义了三个 1×1 卷积，分别为：query_conv、 key_conv、value_conv：

• 在 query_conv 中，输入为 B×C×W×H，输出为 B×C/8×W×H；

• 在 key_conv 中，输入为 B×C×W×H，输出为 B×C/8×W×H；

• 在 value_conv 中，输入为 B×C×W×H，输出为 B×C×W×H。

在 forward 函数中，则定义了 self-attention 的具体步骤：

步骤一：

proj_query  = self.query_conv(x).view(m_batchsize,-1,width*height).permute(0,2,1)

proj_query 本质即加入了 reshape 的操作的卷积。首先对输入 feature map 进行 query_conv 卷积，输出为 B×C/8×W×H；view 函数改变输出维度，就单张 feature map 而言，即将 W×H 大小拉直，变为 1×(W×H) 大小；就 batchsize 大小而言，输出就是 B×C/8×(W×H)；permute 函数则对第二维和第三维进行倒置，输出为 B×(W×H)×C/8。proj_query 中的第 i 行表示第 i 个像素位置上所有通道的值。

proj_key = self.key_conv(x).view(m_batchsize,-1,width*height)

proj_key 与 proj_query 相似，只是没有最后一步倒置，输出 shape 为 B×C/8×(W×H)。proj_key 中的第 j 行表示第 j 个像素位置上所有通道的值。

步骤二：

energy = torch.bmm(proj_query,proj_key)

这一步是将 batch_size 中的每一对 proj_query 和 proj_key 分别进行矩阵相乘，输出特征图 shape 为 B×(W×H)×(W×H)。输出特征图 energy 中的第 (i, j) 是将 proj_query 中的第 i 行与 proj_key 中的第 j 行点乘得到。该步骤的意义是：energy 中第 (i, j) 位置的元素为输入特征图第 j 个元素对第 i 个元素的影响，从而实现全局上下文任意两个元素之间的依赖关系。

步骤三：

attention = self.softmax(energy)

这一步将 energe 进行 softmax 归一化，注意是对行的归一化。归一化后每行之和为1，对于 (i, j) 位置，可理解为第 j 位置对第 i 位置的权重，所有的 j 对 i 位置的权重之和为1，此时得到 attention_map。

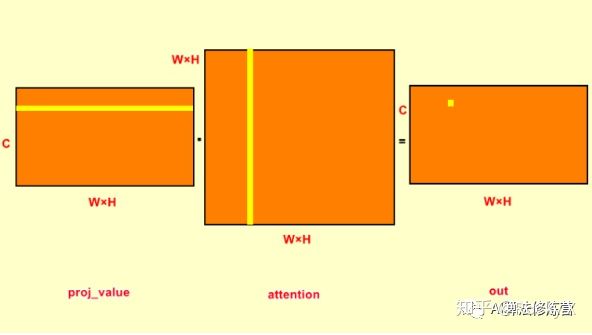
proj_value = self.value_conv(x).view(m_batchsize,-1,width*height)

proj_value 和 proj_query 与 proj_key 一样，只是输入 shape 为 B×C×W×H，输出 shape 为 B×C×(W×H)。从 self-attention 结构图中可知，proj_value 与 attention_map 矩阵相乘，即：

out = torch.bmm(proj_value,attention.permute(0,2,1) )
out = out.view(m_batchsize,C,width,height)

在对 proj_value 与 attention_map 点乘前，先对 attention 转置。这是由于 attention 中每行的权重之和为1，是原特征图第 j 个位置对第 i 个位置的权重，将其转置之后，每列之和为1；proj_value 的每一行与 attention 中的每一列点乘，将权重施加于 proj_value 上，输出特征图 shape 为 B×C×(W×H) 。

步骤四：

out = self.gamma*out + x

这一步是对 attention 之后的 out 进行加权，x是原始的特征图，将其叠加在原始特征图上。系数 gamma 是经过学习得到的，初始值为0。输出即原始特征图，随着学习的深入，在原始特征图上增加了加权的 attention，得到特征图中任意两个位置的全局依赖关系。

---

1.2 Self-attention机制应用：Non-local Neural Networks

论文地址：https://arxiv.org/abs/1711.07971

代码地址：https://github.com/pprp/SimpleCVReproduction/tree/master/attention/Non-local/Non-Local_pytorch_0.4.1_to_1.1.0/lib

在计算机视觉领域，一篇关于 Attention 研究非常重要的文章《Non-local Neural Networks》在捕捉长距离特征之间依赖关系的基础上提出了一种非局部信息统计的注意力机制 —— Self Attention。

文章中列出了卷积网络在统计全局信息时出现的三个问题如下：

1、捕获长范围特征依赖需要累积很多层的网络，导致学习效率太低；

2、由于网络需要累计很深，需要小心的设计模块和梯度；

3、当需要在比较远位置之间来回传递消息时，卷积或者时序局部操作很困难。

故作者基于图片滤波领域的非局部均值滤波操作思想，提出了一个泛化、简单、可直接嵌入到当前网络的非局部操作算子，可以捕获时间(一维时序信号)、空间(图片)和时空(视频序列)的长范围依赖。这样设计的好处是：

• 相比较于不断堆叠卷积和 RNN 算子，非局部操作直接计算两个位置(可以是时间位置、空间位置和时空位置)之间的关系即可快速捕获长范围依赖，但是会忽略其欧式距离，这种计算方法其实就是求自相关矩阵，只不过是泛化的自相关矩阵；

• 非局部操作计算效率很高，要达到同等效果，只需要更少的堆叠层；

• 非局部操作可以保证输入尺度和输出尺度不变，这种设计可以很容易嵌入到目前的网络架构中。

下面我们主要分析一下作者是如何处理长距离信息的。

non-local block

Non-local的通用公式表示：

• x是输入信号，CV中使用的一般是 feature map

• i 代表的是输出位置，如空间、时间或者时空的索引，他的响应应该对j进行枚举然后计算得到的

• f 函数式计算i和j的相似度

• g 函数计算feature map在j位置的表示

• 最终的y是通过响应因子 C(x) 进行标准化处理以后得到的

可以看出，与 Non-local 均值计算相似，i 代表的是当前位置的响应，j 代表全局响应，通过加权得到一个非局部的响应值。

文中有谈及多种实现方式，在这里简单介绍一下在 DL 框架中最好实现的 Matmul 方式 (如上图的 non-local block)：

1. 首先对输入的 feature map X 进行线性映射（说白了就是 1*1*1 卷积，来压缩通道数），然后得到 θ，φ，g 特征；

2. 通过reshape操作，强行合并上述的三个特征除通道数外的维度，然后对θ和φ进行矩阵点乘操作，得到类似协方差矩阵的东西（这个过程很重要，计算出特征中的自相关性，即得到每帧中每个像素对其他所有帧所有像素的关系）；

3. 然后对自相关特征进行 Softmax 操作，得到0~1的 weights，这里就是我们需要的 Self-attention 系数；

4. 最后将 attention 系数，对应乘回特征矩阵 g 中，然后再上扩展 channel 数 (1×1卷积)，与原输入 feature map X 做残差运算，获得 non-local block 的输出。

可能存在的问题 —— 计算量偏大：在高阶语义层引入 non local layer, 也可以在具体实现的过程中添加 pooling 层来进一步减少计算量。

import torch
from torch import nn
from torch.nn import functional as F


class _NonLocalBlockND(nn.Module):
    """
    调用过程
    NONLocalBlock2D(in_channels=32),
    super(NONLocalBlock2D, self).__init__(in_channels,
            inter_channels=inter_channels,
            dimension=2, sub_sample=sub_sample,
            bn_layer=bn_layer)
    """
    def __init__(self,
                 in_channels,
                 inter_channels=None,
                 dimension=3,
                 sub_sample=True,
                 bn_layer=True):
        super(_NonLocalBlockND, self).__init__()

        assert dimension in [1, 2, 3]

        self.dimension = dimension
        self.sub_sample = sub_sample

        self.in_channels = in_channels
        self.inter_channels = inter_channels

        if self.inter_channels is None:
            self.inter_channels = in_channels // 2
            # 进行压缩得到channel个数
            if self.inter_channels == 0:
                self.inter_channels = 1

        if dimension == 3:
            conv_nd = nn.Conv3d
            max_pool_layer = nn.MaxPool3d(kernel_size=(1, 2, 2))
            bn = nn.BatchNorm3d
        elif dimension == 2:
            conv_nd = nn.Conv2d
            max_pool_layer = nn.MaxPool2d(kernel_size=(2, 2))
            bn = nn.BatchNorm2d
        else:
            conv_nd = nn.Conv1d
            max_pool_layer = nn.MaxPool1d(kernel_size=(2))
            bn = nn.BatchNorm1d

        self.g = conv_nd(in_channels=self.in_channels,
                         out_channels=self.inter_channels,
                         kernel_size=1,
                         stride=1,
                         padding=0)

        if bn_layer:
            self.W = nn.Sequential(
                conv_nd(in_channels=self.inter_channels,
                        out_channels=self.in_channels,
                        kernel_size=1,
                        stride=1,
                        padding=0), bn(self.in_channels))
            nn.init.constant_(self.W[1].weight, 0)
            nn.init.constant_(self.W[1].bias, 0)
        else:
            self.W = conv_nd(in_channels=self.inter_channels,
                             out_channels=self.in_channels,
                             kernel_size=1,
                             stride=1,
                             padding=0)
            nn.init.constant_(self.W.weight, 0)
            nn.init.constant_(self.W.bias, 0)

        self.theta = conv_nd(in_channels=self.in_channels,
                             out_channels=self.inter_channels,
                             kernel_size=1,
                             stride=1,
                             padding=0)
        self.phi = conv_nd(in_channels=self.in_channels,
                           out_channels=self.inter_channels,
                           kernel_size=1,
                           stride=1,
                           padding=0)

        if sub_sample:
            self.g = nn.Sequential(self.g, max_pool_layer)
            self.phi = nn.Sequential(self.phi, max_pool_layer)

    def forward(self, x):
        '''
        :param x: (b, c,  h, w)
        :return:
        '''

        batch_size = x.size(0)

        g_x = self.g(x).view(batch_size, self.inter_channels, -1)#[bs, c, w*h]
        g_x = g_x.permute(0, 2, 1)

        theta_x = self.theta(x).view(batch_size, self.inter_channels, -1)
        theta_x = theta_x.permute(0, 2, 1)

        phi_x = self.phi(x).view(batch_size, self.inter_channels, -1)
        
        f = torch.matmul(theta_x, phi_x)

        print(f.shape)

        f_div_C = F.softmax(f, dim=-1)

        y = torch.matmul(f_div_C, g_x)
        y = y.permute(0, 2, 1).contiguous()
        y = y.view(batch_size, self.inter_channels, *x.size()[2:])
        W_y = self.W(y)
        z = W_y + x
        return z	

Non local NN 从传统方法 Non local means 中获得灵感，然后接着在神经网络中应用了这个思想，直接融合了全局的信息，而不仅仅是通过堆叠多个卷积层获得较为全局的信息。这样可以为后边的层带来更为丰富的语义信息。

论文中也通过消融实验，完全证明了该模块在视频分类，目标检测，实例分割、关键点检测等领域的有效性，但是其中并没有给出其带来的参数量上的变化，或者计算速度的变化。但是可以猜得到，参数量的增加还是有一定的，如果对速度有要求的实验可能要进行速度和精度上的权衡，不能盲目添加 non local block。神经网络中还有一个常见的操作也是利用的全局信息，那就是 Linear 层，全连接层将 feature map 上每一个点的信息都进行了融合，Linear 可以看做一种特殊的 Non local 操作。

Non-local Neural Networks模块依然存在以下的不足：

  (1) 只涉及到了位置注意力模块，而没有涉及常用的通道注意力机制

  (2) 可以看出如果特征图较大，那么两个(batch,hxw,512)矩阵乘是非常耗内存和计算量的，也就是说当输入特征图很大存在效率底下问题，虽然有其他办法解决例如缩放尺度，但是这样会损失信息，不是最佳处理办法。

改进思路

---

文献来源：https://zhuanlan.zhihu.com/p/110130098