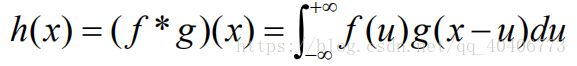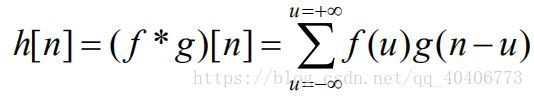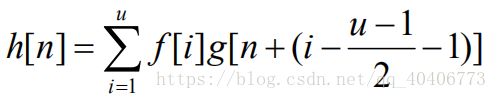加权和、卷积与傅立叶变换三者的关系
1、卷积的定义
若 f(x)和 g(x)是两个连续函数,那么卷积定义为:
其中,h(x)称为f(x)对g(x)的卷积。f 称为卷积核,g 是被卷函数(或者数列)。若 f[n]和 g[n]是两个数列,那么离散卷积定义为:
2、卷积的计算
在 matlab 中,关于两个向量的卷积直接用函数 conv(f,g)即可求得卷积结果。在 Python 中直接调用 numpy 中的 convolve()函数即可。
举个例子,先假设f=[1,2,3], g=[2,3,4],那么f对g的卷积结果计算如下:
当n =1时,h[1]=f[1]*g[1-1]+f[2]*g[1-2]+f[3]*g[1-3] = unknown;
当n = 2时,h[2]=f[1]*g[2-1]+f[2]*g[2-2]+f[3]*g[2-3] = 2;(注意:部分不存在的索引值对应的数列值在计算中默认为0)
当n = 3时,h[3]=f[1]*g[3-1]+f[2]*g[3-2]+f[3]*g[3-3] = 7;
当n = 4时,h[4]=f[1]*g[4-1]+f[2]*g[4-2]+f[3]*g[4-3] = 16;
当n = 5 时,h[5]=f[1]*g[5-1]+f[2]*g[5-2]+f[3]*g[5-3] = 17;
当n = 6时,h[6]= f[1]*g[6-1]+f[2]*g[6-2]+f[3]*g[6-3] = 12;
当n = 7时,h[7]=df[1]*g[7-1]+f[2]*g[7-2]+f[3]*g[7-3] = unknown。
故卷积结果h=f*g=[2,7,16,17,12]。不难得到一般规律,一个长度为m的数列对一个长度为n的数列做卷积得到的新数列长度为n+m-1。
3、卷积与加权和的关系
在程序中,卷积往往作为加权求和的替代物。加权和的公式定义如下:
换言之,当把 f 反向之后,再做离散卷积,那么就与加权和等价。
4、傅立叶变换
离散傅立叶变换的公式如下:
摘自matlab中的帮助代码,其中Y = fft(X), X = ifft(Y), 即Y是X的傅里叶变换,X是Y的逆傅里叶变换。值得注意的是:将一个序列从时域转化到频域(经过傅里叶变换)或者从频域转化到时域(经过逆傅里叶变换),变换前后的序列长度相同。离散傅里叶变换的时间复杂度为O(n*n), 而快速傅里叶变换的时间复杂度为O(n*logn).
5、卷积与傅里叶变换的关系
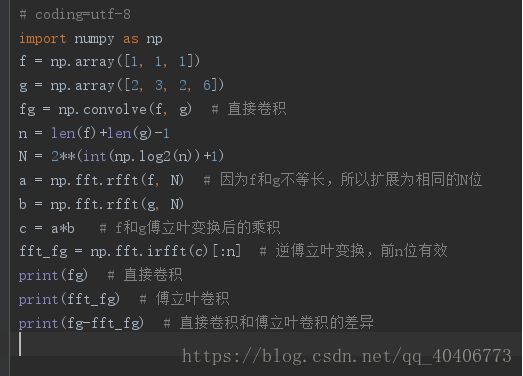
以上为Python的代码展示,将两个数列经过傅里叶变换后在频域上做点积后再做逆傅里叶变换回到时域,其结果与两个向量的卷积是相同的。需要注意的是,在做傅里叶变换将数列从时域转移到频域时,需要对原始数列进行“补0”操作,将数列的长度扩展到至少长度为n+m-1(原因是卷积后的长度就是n+m-1,如果不扩展的话逆变换后得到的长度将不一致,扩展超过n+m-1在逆变换后前n+m-1项即为卷积结果,剩余的都为0)。因此,可形式化为一下公式:
本文主要介绍了加权、卷积及傅立叶变换三者之间的联系。运用 FFT 的优势有:① 加速算法运行。因为加权和,又要加又要乘,计算量是比较大的,而频域的乘法是按位相乘,计算量要小得多。不过实际应用时要权衡傅立叶变换和逆变的时间。② 某些处理在频域很容易(比如屏蔽特定频率)。常规的做法是先做傅立叶变换,处理之后再逆变。如果能够找到与之对应的加权和(卷积),那么就可以直接用加权和(卷积)来计算。例如高斯滤波的实质是过滤高频、低频,保留中频。实际应用中用卷积来实现高斯滤波,因为高斯函数是一种非常特殊的函数,它的傅里叶变换是高斯函数,逆变仍然是高斯函数[1]。
参考资料:
[1] https://blog.csdn.net/liujiboy/article/details/78078392