python3通过scipy实现定积分
本文以几个实际例子讲解scipy求解一重、二重和三重定积分
一、求解一重定积分
问题1:假设函数![]() ,求函数
,求函数![]() 从1到2的定积分,其属下表达式为:
从1到2的定积分,其属下表达式为:
通过python下scipy模块中的integrate下quad函数可以求解该一重定积分。
from scipy import integrate
def f(x):
return x+1
v,err=integrate.quad(f,1,2)#integrate.quad()求一重积分,err是误差
print(v)求解结果为2.5.
通过手算可以发现其结果是正确的:
问题2:假设函数![]() ,假设a=-1,b=1,如何求解下面定积分?
,假设a=-1,b=1,如何求解下面定积分?
在scipy中integrate.quad()函数中可以通过形参args传入函数中,其实现代码如下:
from scipy import integrate
def f(x,a,b):
return a*x+b
v,err=integrate.quad(f,1,2,args=(-1,1))#integrate.quad()求一重积分
print(v)求解结果为-0.5。
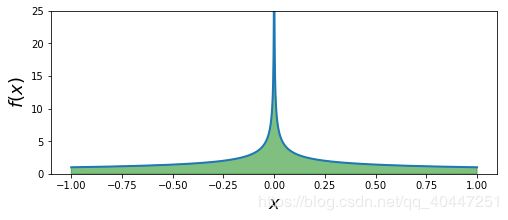
问题3:这里讨论比较棘手的问题:假设函数![]() ,通过绘制该函数的图像,不难看出在
,通过绘制该函数的图像,不难看出在![]() 处存在断点,那么如何求解以下定积分呢?
处存在断点,那么如何求解以下定积分呢?
quad()函数中有points可以跳过断点继续求积分,其实现代码如下:
from scipy import integrate
import matplotlib.pyplot as plt
import numpy as np
def f(x):
return 1/np.sqrt(abs(x))
#绘制图像
fig,ax=plt.subplots(figsize=(8,3))
x=np.linspace(-1,1,10000)
ax.plot(x,f(x),lw=2)
ax.fill_between(x,f(x),color='green',alpha=0.5)
ax.set_xlabel("$x$",fontsize=18)
ax.set_ylabel("$f(x)$",fontsize=18)
ax.set_ylim(0,25)
plt.show()
v,err=integrate.quad(f,-1,1,points=[0])#integrate.quad()求一重积分
print(v)函数图像如下图:
定积分求解结果为3.9999999....
二、求解二重定积分
假设二重积分函数为:
二重积分可通过dblquad()函数进行求解,其实现代码如下:
from scipy import integrate
def f(x,y):
return x*y
def h(x):
return x
v,err1=integrate.dblquad(f,1,2,lambda x:1,h)
print(v)求解结果为1.125.
三、求解三重定积分
假设三重定积分函数为:
三重定积分的求解可通过tplquad()函数进行计算,其实现代码为:
from scipy import integrate
f=lambda x,y,z:x
g=lambda x:(1-x)/2
h=lambda x,y:(1-x-2*y)
v,err=integrate.tplquad(f,0,1,0,g,0,h)
print(v)求解结果为0.020833333333333332。
至此,使用scipy模块对定积分求解的过程到此结束,想要了解更多关于scipy模块的函数可点击链接http://liao.cpython.org/scipytutorial01/。
本文转载自http://liao.cpython.org/scipy18/