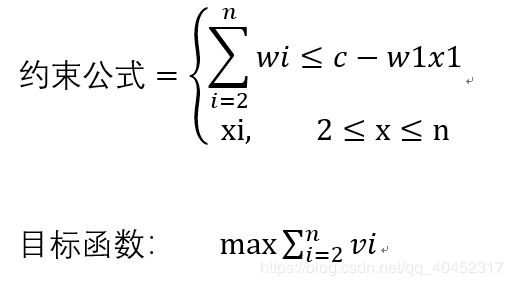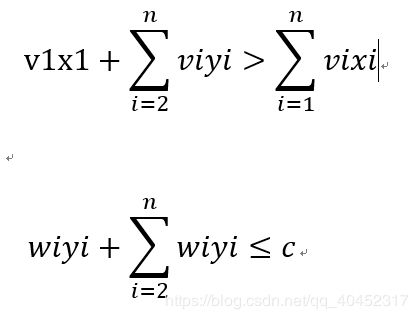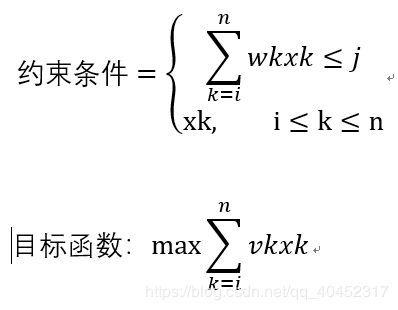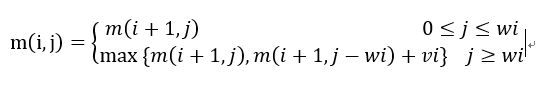算法-动态规划-0/1背包问题
一、动态规划
动态规划(dynamic programming)是运筹学的一个分支,是求解决策过程(decision process)最优化的数学方法。20世纪50年代初美国数学家R.E.Bellman等人在研究多阶段决策过程(multistep decision process)的优化问题时,提出了著名的最优化原理(principle of optimality),把多阶段过程转化为一系列单阶段问题,利用各阶段之间的关系,逐个求解,创立了解决这类过程优化问题的新方法——动态规划。1957年出版了他的名著《Dynamic Programming》,这是该领域的第一本著作。
动态规划本质是进行分治和处理冗杂,适用于解决最优化问题,如最短路径,资源分配,最优装载,库存管理等问题。
基本思想
若要解一个给定问题,我们需要解其不同部分(即子问题),再合并子问题的解以得出原问题的解。 通常许多子问题非常相似,为此动态规划法试图仅仅解决每个子问题一次,从而减少计算量: 一旦某个给定子问题的解已经算出,则将其记忆化存储,以便下次需要同一个子问题解之时直接查表。 这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。
分治与动态规划
共同点:二者都要求原问题具有最优子结构性质,都是将原问题分而治之,分解成若干个规模较小(小到很容易解决的程序)的子问题.然后将子问题的解合并,形成原问题的解.
不同点:分治法将分解后的子问题看成相互独立的,通过用递归来做。动态规划将分解后的子问题理解为相互间有联系,有重叠部分,需要记忆,通常用迭代来做。
二、最优化原理
要采用动态规划求解,必须要求原问题满足最优化原理。
最优化原理(Principle of optimality)最初是由美国数学家R.Bellman等人采用动态规划算法求解多阶段决策问题时提出来的。表述如下:
一个过程的最优决策具有这样的性质:即无论初始状态和初始决策如何,其今后诸策略对以第一个决策所形成的初始状态的过程而言,必须构成最优解。简而言之,一个最优策略的子策略对于其初始状态和终状态而言也必须是最优的。
通俗的来讲就是,子问题的局部最优导致原问题的全局最优解。也就是说一个问题的最优解只取决于他的子问题的最优解。
所以说,使用动态规划必须满足最优化原理。
在分析问题最优化原理时,通常选用的方法是反证法,首先假设由原问题的最优解导出的子问题的解不是最优解,然后,再设法说明在这个假设下可构成比原问题最优解更好的解,从而导致矛盾。
三、0/1背包问题
问题描述
给定n歌物品和一个背包。第i个物品的重量位wi,其价值位vi,背包的总重量位c。如何选取物品装入背包,使得背包所装入的物品总价值最大?(w是重量weight,v是价值value)。
0/1背包问题,在选择物品时,对于物品只有两个选择,一个是装入,一个是不装入。不能装入多次或者装入一部分。
xi表示物品i装入情况,xi=1,即物品你装入,xi=0,即物品没装入。
0/1背包问题的形式可描述为:
0/1背包问题在实际中应用很广泛,如资本预算,货物装载,以及储存分配问题实质都是0/1背包问题。
最优化分析
采用动态规划就是将原问题拆分为若干个规模较小的子问题,通过求解子问题从而实现求解原问题。
假设(x1,x2···xn)是所给问题的最优解。(x2,x3···xn)是下面相应的子问题的最优解。
上述分解过程就是将原问题规模为n的0/1问题分解为n-1个0/1背包问题。接下来可以接续分解知道原问题的规模变为1,这个问题就非常简单,要么装入要么不装入。
采用动态规划,必须满足最优化原理。采用反证法,来证明0/1背包问题是满足最优化原理的。
设(x2,x3···xn)不是上面问题子问题的最优解。则一定存在一个(y2,y3····yn)是上述问题子问题的最优解。因此会有:
这说明(x1,y2····yn)是0/1背包问题的更优解,这与(x1,····xn)是最优解相矛盾。因此,0/1问题满足最优化原理,因此,可以用动态规划。
四、动态规划求解
建立最优值的递归关系:
将上述问题的子问题的最优值存放在m(i,j)中,即表示在背包容量为j,可选物品是i,i+1····n时问题的最优值。也就是放入背包的物品最大值的总和。
m(i=1,j')表示背包容量为j',可选物品为i+1,i+2···n时背包问题的最优值。因此m(i+1,j')是问题m(i,j)问题的子问题,要由m(i+1,j’)得到m(i,j)问题,只要考虑第i个物品是否放入背包。由m(i+1,j')得到m(i,j),分两种情况:
1、如果j'的容量不够放入第i个物品,则m(i,j)=m(i+1,j),表示m(i,j)问题不放入第i个物品。
2、反之,j'容量够放入第i个物品,这时又有两种情况,取其中最大值即可:
1、一种放入该物品,即m(i,j)=m(i+1,j-wi)+vi
2、不放入该物品,m(i,j)=m(i+1,j)
可得以下递推关系:
五、实例
n=5,c=10,w={2,2,6,5,4},v={6,3,5,4,6},求装入背包的最大价值。
算法如下:采用w[1,2,3····n]来存放n个物品的重量,数组v[1,2····n]来存放物品价值,背包容量为c,用二维数组m[i][j]来存放背包容量为j时,可选物品i,i+1···n时的最优值。画图构建m数组:(根据以上公式来计算,自底向上,纵为i,横为j)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 0 | 0 | 6 | 6 | 9 | 9 | 12 | 12 | 15 | 15 | 15 |
| 2 | 0 | 0 | 3 | 3 | 6 | 6 | 9 | 9 | 9 | 10 | 11 |
| 3 | 0 | 0 | 0 | 0 | 6 | 6 | 6 | 6 | 6 | 10 | 11 |
| 4 | 0 | 0 | 0 | 0 | 6 | 6 | 6 | 6 | 6 | 10 | 10 |
| 5 | 0 | 0 | 0 | 0 | 6 | 6 | 6 | 6 | 6 | 6 | 6 |
| w | 2 | 2 | 6 | 5 | 4 | ||||||
| v | 6 | 3 | 5 | 4 | 6 |
得到以上表格,即数组m:
//得到m数组
void Knapsack(int v[M],int w[M],int c,int n,int m[M][M])
{
int jmax=min(w[n]-1,c); //取最小值
//处理自由一个物品的情况,即第n个物品的时候
for(int j=0;j<=jmax;j++)
m[n][j]=0; //当地n个物品不取时,价值为0
for(int j=w[n];j<=c;j++)
m[n][j]=v[n]; //当第n个物品选择时,价值为就是第n个物品的价值
//处理n-1到1层的情况
//每一个m都是根据上一层得出的结果
for(int i=n-1;i>=1;i--)
{
jmax=min(w[i]-1,c);
for(int j=0;j<=jmax;j++)
m[i][j]=m[i+1][j];
for(int j=w[i];j<=c;j++)
m[i][j]=max(m[i+1][j],m[i+1][j-w[i]]+v[i]);
}
}得到最优解x(x1,x2···xn)
//得出最优解(x1,x2···xn)
void Traceback(int m[M][M],int w[M],int c,int n,int x[M])
{
for(int i=1;i总代码:
#include
using namespace std;
#define M 99
int v[M],w[M],m[M][M],x[M];
int min(int a,int b)
{
return a=1;i--)
{
jmax=min(w[i]-1,c);
for(int j=0;j<=jmax;j++)
m[i][j]=m[i+1][j];
for(int j=w[i];j<=c;j++)
m[i][j]=max(m[i+1][j],m[i+1][j-w[i]]+v[i]);
}
}
//得出最优解(x1,x2···xn)
void Traceback(int m[M][M],int w[M],int c,int n,int x[M])
{
for(int i=1;i>n;
cout<<"请输入背包容量:";
cin>>c;
cout<<"请输入物品的重量:";
for(int i=1;i<=n;i++)
cin>>w[i];
cout<<"请输入物品的价值:";
for(int i=1;i<=n;i++)
cin>>v[i];
Knapsack(v,w,c,n,m);
Traceback(m,w,c,n,x);
cout<<"最优解表:"<