基于深度卷积神经网络的图像去噪方法

基于深度卷积神经网络的图像去噪方法

 

摘要：图像去噪在图像处理中仍然是一个具有挑战性的问题。作者提出了一种基于深度卷积神经网络（DCNN）的图像去噪方法。作者设计的不同于其他基于学习的方法：一个DCNN来实现噪声图像。因此，通过从污染图像中分离噪声图像可以实现潜在清晰图像。在训练阶段，采用梯度裁剪方案来防止梯度爆炸，并使网络能够快速收敛。实验结果表明，与现有技术的去噪方法相比，所提出的去噪方法可以实现更好的性能。同时，结果表明，去噪方法具有通过一个单一的去噪模型抑制不同噪声水平的不同噪声的能力。

1.介绍

图像去噪，其目的是从其噪声观察值y中估计潜在干净图像x，对于随后的图像处理非常重要。给定一个加性高斯白噪声模型，它可以表示为：

y = x +z

因此，图像去噪的目标是从中找出x的估计值 y，其中x∈RN表示干净的（未知的）干净图像，其中，表示具有零均值和协方差矩阵σ2I（其中I是单位矩阵）的高斯噪声向量，y∈N表示观察到的噪声图像。

基于滤波的方法[1]，基于扩散的方法[2]，基于总变差的方法[3,4]，基于小波/曲线波的方法[5-7]等，基于稀疏表示的方法[8-11]，基于非局部自相似性（NSS）的方法[11-18]等。在这些方法中，NSS模型在现有方法中很流行。它们表现出很好的去噪效果，特别是对于具有规则和重复纹理的图像。这是因为非局部的基于方法的方法通常对于具有规则和重复纹理的图像更好，而基于区别性训练的方法更好方法通常对不规则纹理或光滑区域的图像产生更好的结果[19]。然而，NSS模型不可避免地存在两个主要缺点[12,17,18]。首先，他们经常需要指定一个特定的去噪功能结果是该算法可能不能对各种图像实施良好的去噪作业。其次，这些模型通常是非凸的，并且涉及多个手动选择的参数，为提高去噪性能提供了一些余地。

为了解决这些问题，最近开发了几种有区别的学习方法来学习图像先验模型，如可训练的非线性反应扩散（TNRD）模型[20]。TNDR模型是通过展开固定数目的梯度下降推断步骤。然而，TNDR模型固有地局限于特定形式的先验。 具体而言，TNRD采用的先例是基于分析模型，该模型在捕获图像结构的全部特征方面有限。

实际上，TNRD模型是一种深度神经网络，可以表示为前馈深层网络。还有一些深度神经网络用于图像去噪[21-23]。Jain和Seung首先使用深度神经网络进行图像去噪[21]。他们声称深度神经网络具有相似或甚至比马尔可夫随机场模型在图像去噪方面具有更好的表示能力。Burger等人提出使用多层感知器（MLP）进行图像去噪[22]。此外，他们将稀疏编码和预先训练过的深度神经网络结合起来去噪自动编码器[23]。尽管这些深度神经网络在图像去噪方面取得了很好的性能，但这些网络并没有有效地探索图像的固有特征，因为它们将类似MLP的网络级联起来。

目前，深度卷积神经网络（DCNN）吸引了越来越多的研究人员，因为它通过大量数据具有很好的自学习能力，不需要严格选择特征，只需要引导学习来达到期望的目的。它被广泛应用于图像预处理领域，如图像超分辨率[24-26]。由于图像超分辨率的成功，一些研究人员尝试将DCNN应用于图像去噪[27-29]。 Lefkimmiatis提出了一种基于非局部图像模型的基于灰度和彩色图像去噪的新型深度网络体系结构[29]。正如作者所声称的那样，所提出的方法确实是一种NSS方法，它利用DCNN学习NSS方法的参数。在[27,28]中，作者直接使用DCNN来实现去噪任务，其中将被污染的图像输入到DCNN中并且输出相应的潜在干净图像。此外，随机梯度下降法被用作训练策略，这将在训练中耗费大量时间。

尽管DCNN成功实现了图像超分辨率，但不能直接用于图像去噪。这是因为图像超分辨率和图像去噪的任务完全不同。对于图像超解决方案，其任务是从丢失了很多的低分辨率图像重建高分辨率图像因此，DCNN可以通过低分辨率图像直接预测高分辨率图像，因为卷积图层可能涉及预测输出图像中的丢失信息。对于图像去噪，其任务是从噪声叠加在原始干净图像上的污染图像中重建潜在干净图像。与噪声图像相比，潜在的干净图像包含更多信息。如果DCNN直接预测像图像超分辨率的DCNN那样的潜在干净图像，则输出图像中的现有信息比噪声图像中存在的信息更复杂。这意味着预测噪声图像的网络的学习负担远远低于预测潜在干净图像的网络的负担。

受噪声分量与污染图像分离的启发[30-32]，我们精心设计了一个DCNN来预测本文中的噪声图像，称为IDCNN。然后，潜在的干净的图像可以通过分离预测来实现来自污染图像的噪声图像。此外，我们讨论网络深度对降噪性能的影响。 此外，还讨论了一些网络参数。最后，我们进行了一系列比较实验来验证所提出的图像去噪方法。

本文的结构如下：在第2节中，我们详细说明了IDCNN的网络体系结构和实现。在第3节中，演示了实验结果和讨论。结论在第4节中提出。

2设计的DCNN的网络结构

卷积神经网络是线性滤波和非线性变换操作的交替序列。输入层和输出层包含一个或多个图像，输出层也可以是矢量。网络的中间层称为隐藏单元，每个隐藏单元的输出称为特征映射。

2.1卷积层和激活功能

在第l卷积层（隐藏单元），先前层的特征映射（xil-1）与卷积核（wijl）卷积，并且输出特征映射（x_j^l）通过激活函数F实现。每个输出特征映射 可以将卷积与多个输入特征图结合起来，制定为：

  

其中Mj表示输入特征图的选择，bj^ℓ表示偏差，*表示卷积算子。

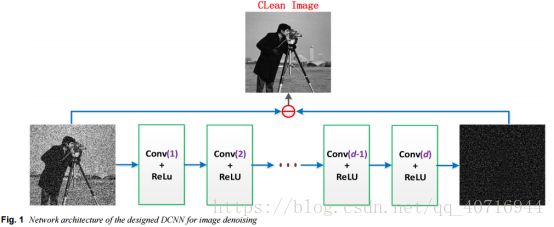
相同的尺寸。其整体结构如图1所示。给定深度d的IDCNN，每一层使用相同的卷积运算。卷积运算实际上是一种线性滤波。卷积运算的线性组合由于其线性特性而不能代表非平凡问题。因此，在DCNN中，非线性激活函数被应用于每个卷积层的输出作为下一层的输入，以便允许这样的网络仅使用少量节点来计算非平凡问题。整流线性单元（ReLU）[33]通常用作DCNN中的激活函数，它是一种非线性映射。已经证明使用整流器作为非线性可以在不需要无监督的预训练的情况下训练深度监督神经网络。与S形函数或类似的激活函数相比，ReLU可以在大型复杂数据集上快速有效地训练深度神经结构。

 

2.2损失函数和梯度裁剪

令X和Y^表示输入被污染的图像和输出噪声图像，分别。给定一个训练数据集{Xi，Yi }_{i= 1}^N，我们的目标是学习一个预测值的模型，其中Y ^是所需干净图像Y的估计值。因此，损失函数是

 

其中θ=[ W，b]是DCNN的网络参数。W是权重矩阵，b是（2）中定义的偏向量。我们的目标是最小化损失函数以找到DCNN的最优参数θ。

显然，最小化F(θ)是解决非凸优化问题。随机梯度下降法通常用于解决这个优化问题，它通过反向传播不断调整和优化网络参数。我们试图用随机梯度下降来训练提出的DCNN。不幸的是，在我们提出的网络中，我们发现无论如何调整学习速率和其他网络参数，网络几乎不会收敛，网络性能也不好。当学习率> 0.01时，网络甚至不能收敛。这表明随机梯度下降在我们提出的网络中使用时可能导致梯度爆炸。为了避免这些问题，常用的策略之一是将单个渐变剪裁到预定范围[-β，β]。因此，在训练过程中，梯度保持在一定范围内。我们使用给定的渐变裁剪方案阈值[34,35]。假设给定的梯度阈值为β，则当前梯度值为g。如果| | G | | ≥β，那么

 

因此，当训练期间当前梯度值超过给定阈值时，将当前梯度值分配给

（β/ || g ||）g。所以，梯度在固定范围内变化，以便设计的DCNN快速收敛。

2.3设计的网络架构

设计的网络结构如图1所示。一个大小为43×43的污染图像被输入到设计的DCNN中，相应的输出是预测的噪声图像，输出的尺寸是43×43。深度的本文设计的网络设置为10。在设计的DCNN中有几个卷积层，但没有池化层。在每个卷积层中，有64个5×5卷积核。

众所周知，增加感受域的大小可以利用更大图像区域中的上下文信息[21]。在这里，感受野在CNN中在空间上是连续的。CNN通过强化相邻层神经元之间的局部连通性模式来利用空间局部相关性[36]。换句话说，第m层中的卷积层的输入是第（m-1）层中卷积层的子集的输出。因此，形成了空间上连续的感受野。然而，每个卷积层对于输入之外的感受域之外的变化没有响应，这确保学习的卷积核对空间局部输入模式产生最强响应。然而，我们可以堆叠许多这样的层以使卷积核变得越来越全球化（即，响应于更大的像素空间区域）。换一种说法，随着网络深度的增加，感受野的大小增加。假设我们对所有图层使用n×n相同大小的卷积核。对于第一层，接受场的大小是n×n。对于第二层，大小感受野在高度和宽度上增加（n-1）等等。因此，如果设计的DCNN的深度是d，其感受野是[（n-1）d + 1]×[（n-1）d + 1]。

由于实验平台的局限性，设计的DCNN的深度d被设置为10.似乎卷积核的尺寸越大，设计的DCNN的接收场的尺寸越大，其中固定深度是并且设计的DCNN实现更好的性能。但值得一提的是，所有卷积操作都不使用零填充来避免训练期间的边界效应。在测试阶段，所有的卷积层都有足够的零填充。因此，过零填充会导致严重失真。而且，尺寸较大的卷积核与较小尺寸的卷积核相比，会导致较大的计算负担[26]。因此，卷积核的适当大小有助于设计的DCNN。在这里，我们将卷积核的大小设置为5×5。如上面的段落所示，接受但为了确保网络在训练过程中具有良好的灵活性，我们选择了尺寸为43×43的输入图像。我们还进行了一个实验来验证输入训练与那些尺寸为43×43的图像相比，可以实现良好的性能其他尺寸。详情请参阅第3.4节。

每个卷积层上的更多卷积核可以获得更多的特征映射，这表明可以表示输入图像的更多潜在特征。然而，超过一定水平的特征映射太多会使训练过程在数值上不稳定[37]。64个卷积核通常用于大多数DCNN [24,26]。所以，我们在每个卷积层也使用64个卷积核。

 

3实验结果和讨论

3.1设计的DCNN的实现

我们使用Caffe [38]来训练设计的DCNN。Caffe是一个深思熟虑的表达，速度和模块化的深度学习框架。它是一个完全开源的框架，可以提供对深层体系结构的明确访问。它的代码是用干净，高效的C ++编写的，CUDA用于GPU计算，以及几乎完整的支持Python / Numpy和MATLAB的绑定。使用协议缓冲区语言将Caffe模型定义写为配置文件。使用Caffe训练DCNN时，网络架构和训练参数预先配置为配置文件。如果有新图层的话在原有的Caffe框架中不存在的都是在DCNN中添加的，他将与这些新层相关的代码编入原来的Caffe框架中。

在实验中，动量和重量衰减参数分别设为0.9和0.0001。采用[39]中描述的方法来初始化权重。

所有的实验都是通过一台带有NVIDIA Quadro K4200 4G，CPU Intel Xeon E5-2630 @ 2.3 GHz和16 GB内存的图形工作站进行的。我们使用MatConvNet软件包[40]进行了比较实验。

3.2数据预处理和度量

在下面的实验中，从数据集[41]和伯克利分割数据集[42]中选择的图像被用来构建训练数据集。图像通过旋转和缩放来增强。为了简单起见，所有图像都转换成灰度图像。具有不同噪声水平的高斯噪声叠加到所有图像上。图像由43×43像素的滑动窗口裁剪，两个相邻子图像之间的滑动距离为14像素。该值位于重叠窗口中的像素对于两个相邻的子图像是相同的。因此，这些裁剪的子图组成了训练数据集。

采用峰值信噪比（PSNR，以dB为单位）作为评估去噪方法性能的指标。

3.3设计的DCNN的非固定噪声掩膜

通常，在DCNN方法中，具有相同噪声水平的训练污染图像通常使用固定噪声掩模[23]。换句话说，ε是（1）中的固定矩阵。但是，我们发现具有非固定噪声掩码的训练数据集可以与固定噪声掩模相比，表现更好。也就是说，对于我们的训练数据集，对于每个噪声水平，ε是（1）中的非固定矩阵。

为了证明非固定噪声掩模的优势，我们进行了一项实验，以比较设计的DCNN针对固定和非固定噪声掩模所实现的去噪性能。从[41]中选择的91个图像按3.2节所述进行预处理以组成训练数据集。如图2所示，选择三个图像进行测试，分别是'摄影师'，'家'和'莉娜'。不失一般性，我们将噪声水平设为δ= 20。我们设定了设计的深度 DCNN到10。图3说明了由固定和未固定噪声掩模设计的DCNN实现的去噪结果。如图3所示，可以看出，使用非固定噪声掩模设计的DCNN比使用固定噪声掩模的DCNN具有更好的去噪性能。

 

3.4初始学习率

学习率对于所提议的网络的收敛是重要的。我们进行了一个实验来讨论初始学习率对网络性能的影响。培训和测试数据与第3.3节所述的相同。我们相应地将初始学习率设置为0.2,0.1,0.01和0.001。在每20个训练时期后，他们减少0.1。如图4所示，设计的具有梯度限幅的DCNN可以在不同的初始学习速率下获得良好的收敛性和良好的去噪效果。当初始学习率为0.1时，设计的DCNN达到最佳收敛。事实表明，通过调整初始学习速率，我们可以实现（3）中的优化问题函数的近似最优解，尽管梯度限幅不能保证全局最小。 

 

3.5设计的DCNN的深度和输入训练图像的大小

为了研究设计的DCNN的性能与其深度之间的关系，我们进行了一些实验，其中设计的DCNN的深度被设置为4,6,8和10.由于我们的计算性能的限制 硬件，为了方便起见，我们将网络的最大深度设置为10。训练和测试数据与第3.3节所述的相同。如表1所示，网络深度越大，PSNR的值越高，这意味着所提出的去噪方法实现的性能越好。该主观评估也验证了这一事实，如图5所示。然而，网络的深度通常意味着更多的参数，这使得扩大的网络更容易出现过度拟合[43]。所以，一个适当的深度网络对融合和网络性能非常重要。

输入训练图像的大小与卷积核的大小和网络的深度有关。我们进行了一个实验来证明输入训练图像的大小对设计的DCNN的去噪性能的影响。在这里，我们设置网络深度为10，卷积核的大小为5×5。我们用不同大小（20×20,43×43,96×96）的输入图像训练了设计网络。第一种和第三种尺寸分别在[27,28]中使用。第二个被认为是合适的大小在本文中。在实验中，被污染图像的噪声水平均为σ= 20。同时，选择PSNR作为度量。如表2所示，输入43×43的训练图像的设计网络达到最佳去噪结果。事实验证43×43是设计网络输入训练图像的适当大小，这在2.3节中讨论。

3.6几种噪声级别的单一模型

我们发现，单个模型提出的去噪方法能够同时抑制不同噪声水平的不同噪声。这意味着具有不同噪声水平的图像可以作为训练集被同时输入，因此我们可以使用训练过的单一网络模型去除具有不同噪声水平的图像中存在的噪声。

在这里，我们进行了实验来验证网络的这一特性。 培训和测试数据与第3.3节所述的相同。噪声水平δ= 15,20和25时，图像受到不同噪声的污染。在实验中，我们独立训练设计的DCNN相对于不同的噪声等级，相应地在表3中分别表示为Model_15，Model_20和Model_25。为了说明单个模型对于多个噪声水平的能力，设计的DCNN也通过同时输入具有不同噪声水平的训练对来训练，在表3中表示为Model_mixture。显然，与混合模型相比，Model_mixture也可以实现相当好的去噪性能 独立训练的模型。

 

3.7拟议方法与最先进方法之间的比较

在本节中，我们将对18个广泛使用的自然图像进行比较实验（如图6所示）。 标准偏差σ= 15,25,50的高斯白噪声被添加到那些测试图像中。我们训练设计的DCNN超过60个时期（每个时期包括9771次迭代，批量大小为64）。

 

为了验证所提出的去噪方法，我们将其与几种最先进的去噪方法（包括BM3D [12]，EPLL [27]，WNNM [17]，加权Schatten p-范数最小化（WSNM）[18] ，MLP [22]和TNRD [19]。这些比较方法的实现代码由相应的作者提供，可以从作者的网站下载。请注意，由[22]中的方法实现的噪声水平δ= 15的去噪结果未提供，因为作者没有提供具有此噪声水平的模型。对于我们提出的方法，我们通过3.6节所示的两种方案来训练设计的DCNN。一个训练对由每个噪音水平独立训练。然后，训练的DCNN用于抑制具有相同噪声水平的噪声。在这里，我们将这个降噪模型称为IDCNN-1。另一个是通过同时输入具有不同噪声水平的训练对来训练的。然后，训练的DCNN用于抑制具有不同噪声级别的噪声。我们将此降噪模型称为IDCNN-2。

如表4-6所示，每个图像的每个噪声级别的最佳PSNR以粗体突出显示。可以看出，与其他去噪方法相比，所提出的去噪方法，特别是IDCNN-1，可以实现大部分图像的最佳性能。这是因为DCNN对于大量的训练数据具有良好的学习能力，并且探索了图像中存在的固有特征。IDCNN-2也能实现很好的去噪效果，尽管它只是一个噪声级别的单一模型。特别是，IDCNN-2在几种图像中实现了最佳的去噪性能，噪声水平δ= 50。这表明IDCNN-2对图像具有很好的泛化能力降噪。不幸的是，我们的方法不能仅在两个图像'House'和'Barbara'具有每个噪声级别时才能实现最佳性能。正如文献[19]所推论的，BM3D和NSS方法（这里是WNNM和WSNM）是内部去噪方法，在主要是具有规则和重复纹理的图像上，其优于外部去噪方法。学习方法（这里是MLP，TNRD和IDCNN）和EPLL是外部去噪方法[19]。但是，对于包含平滑区域或不规则纹理的图像，外部去噪方法优于内部去噪方法。这里有两个例子在图7中对平滑区域或不规则纹理与规则和重复纹理进行了说明。虽然[22]和TNRD中的MLP是深度神经网络，但我们提出的方法也比这两种方法获得更好的去噪性能。这是因为与我们设计的DCNN相比，这两种方法并没有有效地探索图像的固有特性，因为它们级联了类MLP网络。

另外，我们在表4-6中说明每种方法的运行时间。WNNM和WSNM方法是两种NSS方法，它们应该找到非凸模型的解。这会导致沉重的计算负担。 因此，WNNM和WSNM方法消耗表中方法中的运行时间最多。EPLL方法涉及最大后验估计以在每次迭代中更新图像块。这个操作会导致EPLL方法在计算速度上不好。BM3D是一种基于过滤的去噪方法。所以，这是非常耗时的。TNRD和IDCNNs也取得了相当好的计算性能，因为这些方法是端到端的学习方法。

选择两个例子来说明通过不同方法去噪视觉表现（如图8和9所示）。 图8说明了在噪声水平δ= 25的情况下通过不同方法获得的视觉结果，并且图9表示噪声水平δ= 50的情况下的视觉结果。每个图像的一小部分被放大并显示以用于清晰显示，这是由一个突出显示的红色窗口标记。从图8和图9可以看出，与其他IDCNN-1和IDCNN-2相比，它可以实现很好的去噪效果并且很好地重建了潜在的清晰图像去噪方法，特别是由于保留尖锐的边缘和细节。因此，视觉效果评估的对比实验与上述客观评估一致，验证了我们提出的去噪方法的有效性。

 

4、结论

在本文中，我们提出一种基于深度卷积神经网络的图像去噪方法，称为IDCNN。与其他最先进的学习方法不同，所设计的DCNN在污染图像输入网络时预测噪声图像。然后，通过将预测噪声图像与污染图像分离来实现潜在清晰图像。 我们进行了一些实验来探索设计的DCNN的特性。我们发现网络的深度越大，所提出的去噪方法的性能越好。此外，提出了一种单一模型的去噪方法具有同时抑制不同噪声级别的不同噪声的能力。对比实验结果验证了该方法的良好去噪能力，表明它为图像去噪提供了一种有效的解决方案。