先阐述一下向量的概念和公式,再结合例子去验证这些公式
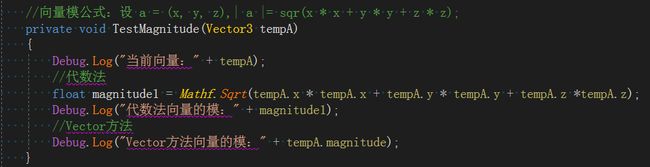
1、向量的模:向量的大小就是向量各分量平方和的平方根。
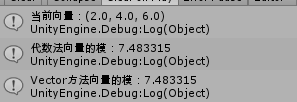
向量的模公式: 设 a = (x, y, z),|a|= sqr(x * x + y * y + z * z);
对应unity中的Vector3.magnitude;比较模的大小时,用Vector3.sqrMagnitude,表示模的平方,这样少了一个开根号的运算。
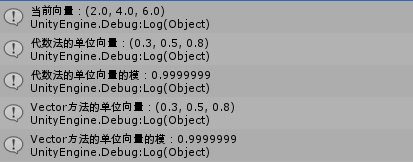
2、单位向量:模等于1的向量,用向量的模分之一乘以原向量,设向量a,则单位向量 n=a/|a|
对应unity中的Vector3.normalized
3、向量的距离公式: 设 a = (x1, y1, z1),b=(x2,y2,z2),距离dis=sqr((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1)+(z2-z1)*(z2-z1))
对应unity中的Vector3.Distance(a,b)
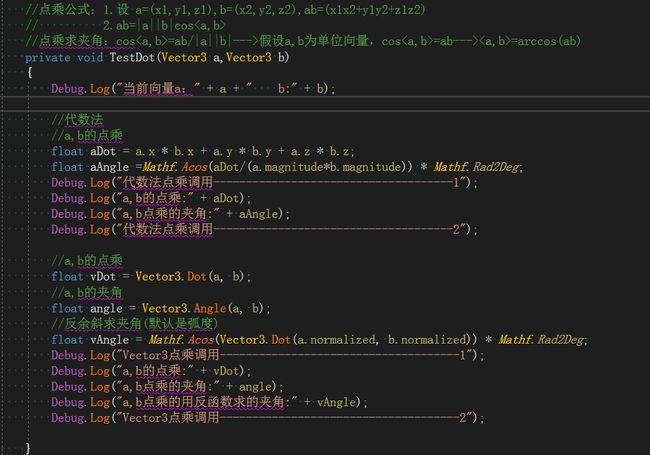
4、向量的点乘:对应分量乘积的和,结果是一个标量,不是一个向量
点乘公式:设 a = (x1, y1, z1),b=(x2,y2,z2), ab=x1*x2+y1*y2+z1*z2
性质1: ab = |a||b|Cos(θ) ,θ是向量a和向量 b之间的夹角。
性质2:ab = ba满足乘法交换律
求夹角公式:Cos(θ) =ab/|a||b|,假设a,b为单位向量,Cos(θ) =ab---->θ=arccos(ab)。反余弦值域在【0,180】
点乘结果符号的判断:ab>0,角度[0,90),a,b向量方向基本相同;ab=0,角度等于90,a,b向量正交;ab<0,角度(90,180],a,b向量基本相反
总结: 通过上述验证发现,Vector3.Angle和利用点乘的性质反余弦函数求出的角度是一样的。而且这两种方法求出的角度区间都是[0,180],所以想要知道真实旋转角度,旋转自身到达另一个向量的角度,需要叉乘的配合。通过上面两种情况的点乘图发现,点乘的值>0,两个向量方向基本相同,点乘的值<0,两个向量方向基本相反。
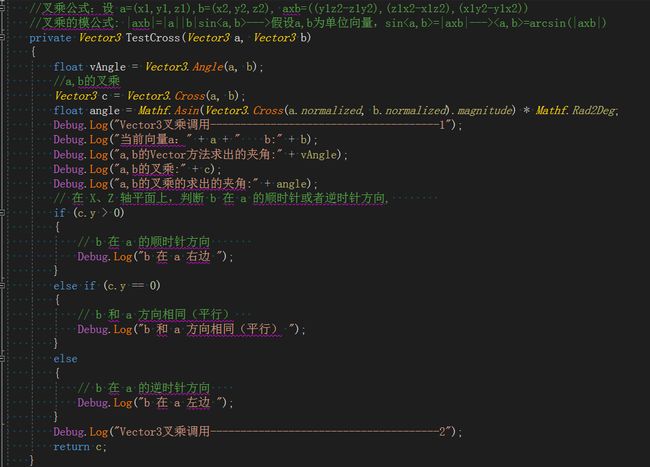
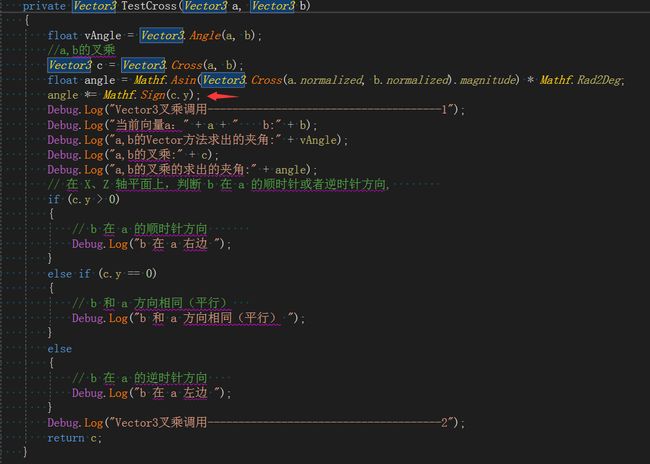
5、向量的叉乘:叉乘得到的是一个向量,不满足交换律。c=axb,c垂直于a,c垂直于b
叉乘公式:设 a=(x1,y1,z1),b=(x2,y2,z2), axb=((y1z2-z1y2),(z1x2-x1z2),(x1y2-y1x2))
叉乘的模公式: |axb|=|a||b|sin(θ)
注意:不要用叉乘求向量的夹角,因为反正弦函数的值域在[-π/2,π/2],下面验证一下,我以xz为平面,分别计算4个象限的向量夹角
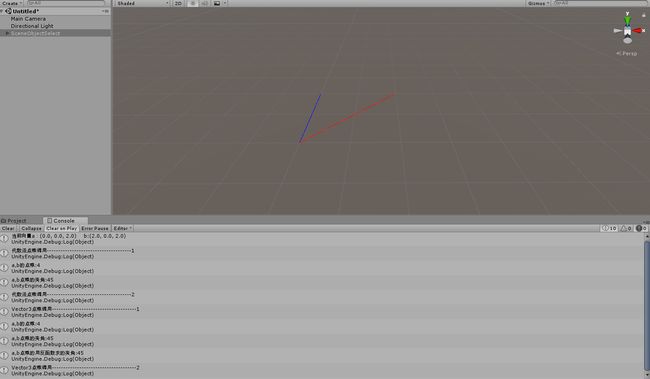
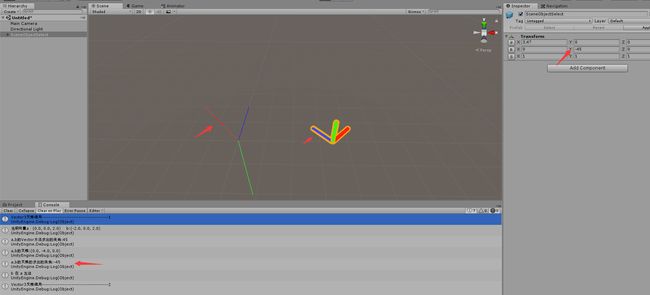
(1)向量a,b在第一象限
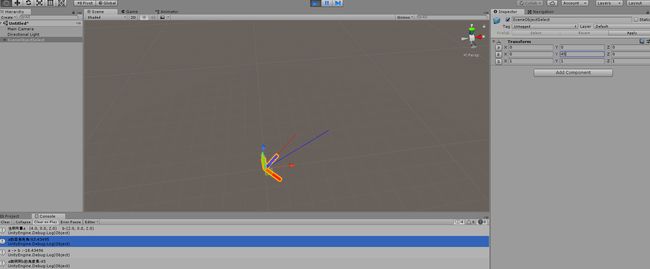
注:场景中SceneObjectSelect这个是搭的坐标系,方便观看
由图可见,Vector3.Angle,Vector3.Cross算出的角度都是45度,并且场景物件直接赋值和b向量方向是平行的。根据叉乘的结果也可以看到向量b在向量a的右边。
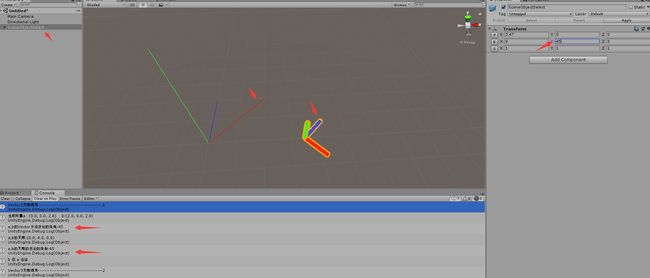
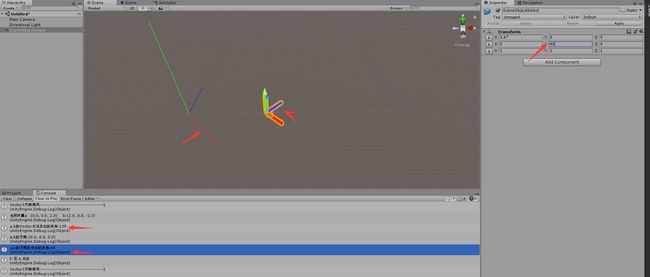
(2)向量a,b在第二象限
由图可见,Vector3.Angle,Vector3.Cross算出的角度都是45度,但是向量b在向量a的左边,如果旋转a也是加上一个负值,这里再把叉乘算出的方向和角度结合一下。看一下下面的代码。
这里发现给角度加上方向的判断,就正确了。看到这里大家是不是觉得,叉乘即能算角度,又能判断方向,那要点乘干嘛?我当时也有这个困惑,直接在验证第三象限的时候,发现自己给误导了。
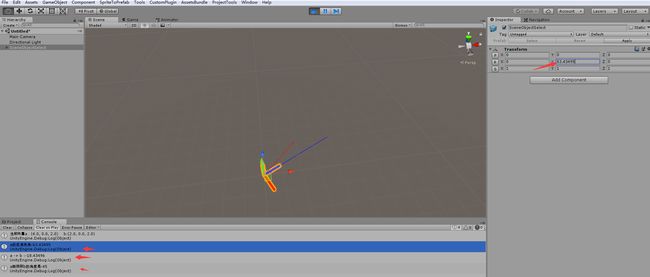
(3)向量a,b在第三象限
在这个图中看出,向量b在第三象限,Angle方法算出的是135度(因为范围区间【0,180】),叉乘的夹角是-45度,这不对啊。我手动调了下数值,应该是-135度,才能和向量b平行。最后查到的原因是ArcSin反正弦函数的值域居然在[-π/2,π/2],是不可能算出135度的,关于反函数的知识自行百度。所以这里我认为不能用叉乘算角度。我们再看看第四象限的情况。
(4)向量a,b在第四象限
这个图中看出,向量b在向量a的右边,Angle方法算出的是135度,叉乘的夹角是45度。还是不对的,所以我觉得叉乘求出的角度不能直接拿来用,反而点乘和Angle方法算出的夹角是对的,但是得不到负的角度。
总结:这里验证的时候,为了直观的观察,向量a用了特殊向量,是在坐标轴上的向量,这里也推导了叉乘求出的角度不能用。后面我用了非坐标轴上的向量a,b,更能直观的看出叉乘的角度不能用。
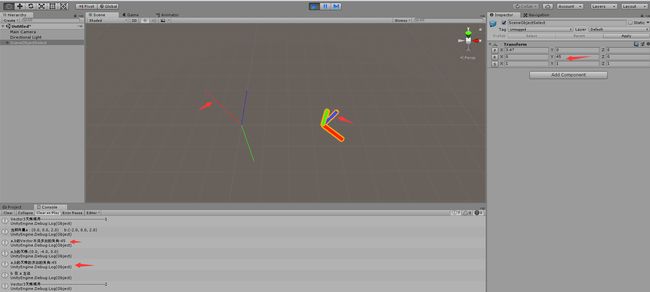
a->b的夹角(包含方向旋转)
SceneObjectSelect指向的是向量a
求出的夹角是-18.43496,是带方向的角度。所以a旋转到b时,只要自身角度加上这个夹角。
总结:点乘判断角度,叉乘判断方向。如果正在看的大佬发现有什么问题,请指出,我及时修改,大家一起学习。