八数码(Eight Digits)问题:宽度优先搜索、全局择优搜索、A*算法(C语言实现)
八数码(Eight Digits)问题
For WHUTers, 今天带大家用C语言应用三种算法求解八数码问题,
三种算法的实现代码,我已放到我个人的github仓库上,github地址:https://github.com/RaySunWHUT/Eight-Digits,欢迎大家star、 fork!
1. 问题描述
这里需要说明的是,八数码的起始阵列与目标阵列可以是任意的。
1.1 判断结点的可达性
定理:
\quad 只有具有同奇或同偶逆序排列的八数码才能移动可达,否则不可达。
这里主要通过判断两结点的逆序数是否同奇或同偶来判断节点的可达性。
2. 数据结构设计

这里采用 3 * 3 的二维数组存储八数码阵列(空格位置用0填充)。
const int standard[3][3] = { {1, 2, 3}, {8, 0, 4}, {7, 6, 5} };
此处也可以采用一维数组表示,此处用二维数组的原因是更利于逻辑上的理解和思考。
此处,定义结构体“九宫格(Nine)”,表示八数码阵列:
typedef struct Nine { // 数据结构: 九宫格
int digit[3][3]; // 九宫格阵列
int zero[2]; // "0" 的横、纵坐标:zero[0] = x(横坐标); zero[1] = y(纵坐标);
Direction blockDirection; // 禁止方向, 防止回退形成死循环
struct Nine* parent; // 父节点指针
} Nine, * Ipointer;
其中Direction为用枚举类型(enum)表示的结构体:
typedef enum Direction { // 数据结构: 移动的方向
UP,
DOWN,
LEFT,
RIGHT,
NONE
} Direction;
为方便后文表示,此处用枚举(enum)类型定义bool数据类型。
bool类型定义如下,
typedef enum bool { // 自建bool型
False = 0,
True,
Unknown
} bool;
3. 核心算法设计
核心算法部分分别采用3种算法解决八数码问题:
- 宽度优先搜索;
- 全局择优搜索;
- A*算法;
\quad 首先,无论采用哪种算法,都会有一个必不可少的步骤,那就是移动滑块"0";
所以,首先来看下,移动滑块的函数move():
bool move(Ipointer node, Direction way) { // 移动 "0"
int x, y; // 存储 滑块"0" 的横、纵坐标
x = node->zero[0];
y = node->zero[1];
int mx = x; // 移动后的x坐标
int my = y; // 移动后的y坐标
bool flag = False; // 标记是否可移动
switch (way) { // 选择方向
case UP:
if ((--mx) >= 0) {
flag = True;
}
break;
case DOWN:
if ((++mx) <= 2) {
flag = True;
}
break;
case LEFT:
if ((--my) >= 0) {
flag = True;
}
break;
case RIGHT:
if ((++my) <= 2) {
flag = True;
}
break;
}
if (flag == True) { // 可移动
int location = node->digit[mx][my]; // 进行结点元素交换
node->digit[x][y] = location;
node->digit[mx][my] = 0;
node->zero[0] = mx; // 赋值父节点"0"坐标
node->zero[1] = my;
node->blockDirection = getBlockDirection(way); // 赋值回退方向
} else {
free(node); // 不可移动, 则释放该结点
}
return flag; // 返回移动结果
}
\quad 滑块移动函数move(),即对滑块进行上、下、左、右四个方向的移动,如果可移动,则返回True,否则返回False。
\quad 在实现三种算法进行搜索之前,判断当前结点与目标结点的逆序数是否同奇或同偶,若不是,则目标状态不可达,算法结束!
在滑块移动函数move()的基础上,我们分别实现了三种搜索算法:
3.1 宽度优先搜索(Breadth First Search)
3.1.1 算法描述
\quad 宽度优先搜索(Breadth First Search)是一种盲目搜索算法,即,蛮力法;算法描述如下:

这种先进先出(FIFO)的算法,我们自然而然的想到,应该用队列(Queue)来描述。
3.1.2 核心数据结构定义
typedef struct Node { /* 数据结构: 队列中的结点 */
ElementType Data;
struct Node* Next;
} Node, * Npointer;
typedef struct Queue { // 队列
Npointer Front, Rear; /* 队头,队尾指针 */
int MAXSize; /* 队列最大容量 */
int standard[3][3]; /* 标准九宫格 */
int inversion; /* 标准九宫格的逆序数 */
long unique; /* 标准九宫格布局转换的long型串 */
} Queue, * Qpointer;
3.1.3 核心算法
void searchFollow(Qpointer open, Ipointer begin) { // 寻找后继节点
Ipointer node = NULL;
for (Direction way = UP; way <= RIGHT; way++) { // 尝试 "上、下、左、右" 所有四个方向, 判断是否可移动
if (way != begin->blockDirection) { // 非回退方向
node = createNode(begin); // 依据父节点创建新节点
bool flag = move(node, way); // 移动"0", 为新节点产生新布局
if (flag == True) { // 若能够产生新布局, 即, 可移动
node->parent = begin; // 赋值回溯指针
if (judgeParity(countInverseNumber(assistInverse(node->digit)), open->inversion)) {
addQ(open, node);
}
}
}
}
}
3.2 全局择优搜索(Global Optimization Search)
3.2.1 算法描述
\quad 全局择优搜索(Global Optimization Search)属于启发式搜索,即利用已知问题中的启发式信息指导问题求解,而非蛮力穷举的盲目搜索。
启发式信息:即,可用于指导搜索过程,且与具体问题求解有关的控制性信息。
\quad 用于描述启发式信息的数学模型,称为启发函数,根据问题特点和看待问题的角度不同,同一问题,可以定义多个启发函数。
\quad 此处,启发函数定义为:f(n) = d(n) + h(n),其中d(n)表示当前结点的深度,h(n)表示定义为当前节点与目标节点差异的度量,即当前节点与目标节点格局相比,位置不符的数字个数。
具体算法描述如下,

\quad 由于全局择优算法,不是简单的将新产生的结点直接加入队列尾,而是按照估计函数值的大小,重新排序队列,故,应采用优先队列(priority queue) 实现。
ps:此处为用C语言手动实现的最小堆(MinHeap)。
3.2.2 核心数据结构定义
typedef struct Nine { // 数据结构: 九宫格
int digit[3][3]; // 九宫格阵列
long unique;
int zero[2]; // "0" 的横、纵坐标:zero[0] = x(横坐标); zero[1] = y(纵坐标);
Direction blockDirection; // 禁止方向, 防止回退形成死循环
struct Nine* parent; // 父节点指针
int weight; // 节点权重
} Nine, * Ipointer;
typedef struct Heap { // 最小堆
ElementType* data; /* 存储元素的数组 */
int size; /* 堆当前元素的个数 */
int capacity; /* 堆的最大容量 */
int standard[3][3]; /* 标准九宫格 */
int inversion; /* 标准九宫格的逆序数 */
long unique; /* 标准九宫格布局转换的long型串 */
} Heap, * Hpointer;
typedef Hpointer MinHpointer;
\quad 由于启发函数定义为 f(n) = d(n) + h(n),其中d(n)表示当前结点的深度,h(n)表示定义为当前节点与目标节点差异的度量,即当前节点与目标节点格局相比,位置不符的数字个数。
\quad 所以,结点估计值f(n) 越小,搜索路径越短,越有可能找到目标结点,故采用 最小堆(MinHeap) 实现算法。
故,启发式函数getWeight()如下,
void getWeight(MinHpointer open, Ipointer node) { // 获取权重, 权重越小, 越先达到目标状态
int diff = 0; // 记录不同元素个数
int deep = 0; // root为 1 层
int weight = 0;
Ipointer p = node;
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
if (node->digit[i][j] != open->standard[i][j]) {
diff++;
}
}
}
deep = getDeep(node);
weight = diff + deep; // 权重越小(即, 浅 + 少, 深度约浅、不同元素越少), 相似度越高, 路径越短
node->weight = weight;
}
3.2.3 核心算法
void globalOptimizationFollow(MinHpointer open, Ipointer begin) {
Ipointer node = NULL;
int k = 0;
for (Direction way = UP; way <= RIGHT; way++) { // 尝试 "上、下、左、右" 所有四个方向, 判断是否可移动
if (way != begin->blockDirection) { // 非回退方向
node = createNode(begin); // 依据父节点创建新节点
bool flag = move(node, way); // 移动"0", 为新节点产生新布局
if (flag == True) { // 若能够产生新布局, 即, 可移动
if (judgeParity(countInverseNumber(assistInverse(node->digit)), open->inversion)) {
node->parent = begin; // 赋值回溯指针
getWeight(open, node);
insertElement(open, node);
}
}
}
}
}
3.3 A* 算法(A Star)
3.3.1 算法描述
\quad 实际上,全局择优搜索(Global Optimization Search)就是A算法,而A*算法即是A算法的下界。
\quad 此处,A*算法是在A算法的基础上,每生成一个新节点,即查找closed表,如果closed表中有相同排列的结点,那么则比较他们的权重(f(n)),如果新节点的权重更小,则替代原结点,即,刷新原结点的深度,这样就很有可能找到更短、更快的到达目标结点的路径。
所以, A*算法相较于全局择优搜索(Global Optimization Search)算法,改动非常小,只增加了部分函数。
3.3.2 核心算法
void applyAStar(Cpointer closed, Ipointer node) { // 应用A*算法
Ipointer resultp = findUnique(closed, node);
if (resultp != NULL) {
if (getDeep(resultp) > getDeep(node)) {
resultp->parent = node->parent;
resultp->weight = node->weight; // 有必要更新
}
}
return;
}
ok,结束!
4. I/O operation
Input:
此处的输入格式:文件格式,文本为数字序列。
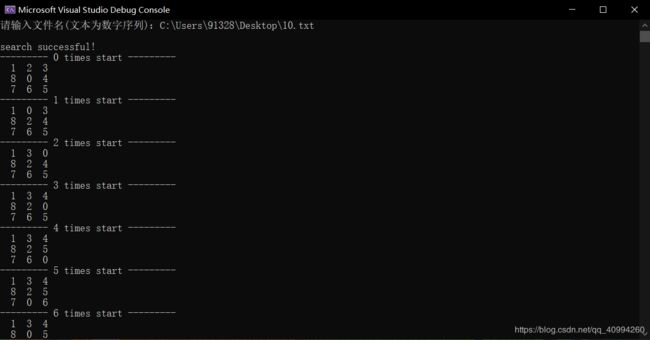
5. 结果展示
[博客为博主原创,如有任何错误,还请大家指正,以免误人子弟!]