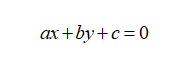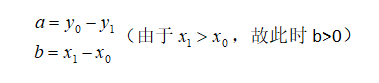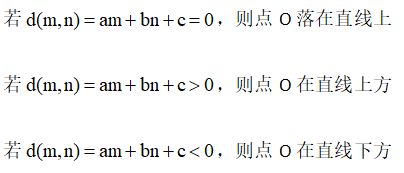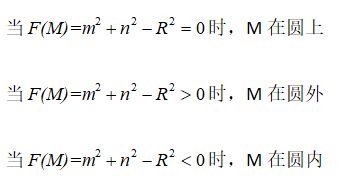计算机图形学第一次上机——中点线算法和中点圆算法

 

计算机图形学第一次上机实验 课程实验报告

 

---

目录

计算机图形学第一次上机实验 课程实验报告

一、实验目的

二、实验环境

三、实验内容

1.中点线算法

2.中点圆算法

四、实验心得

附录：程序源代码

---

一、实验目的

1. 掌握配置glut库的步骤
2. 测试运行示例代码
3. 掌握并编写中点线算法和中点圆算法

二、实验环境

1.codeblocks-17.12

2.Windows10 SDK 10.0.17134.0

CodeBlocks是一款轻量级的IDE，大小只有几十MB，我觉得用起来比较方便，而且配置glut库的时候也简单，所以就用了CB，能实现和Dev c++相同的功能。

 

三、实验内容

1. 简单图元的绘制

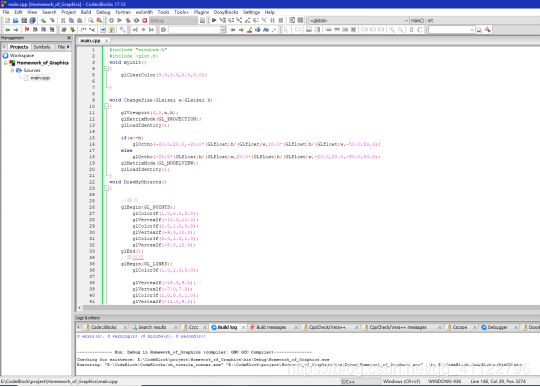
1. 在CB中新建glut工程，将lec3文件夹的drawGeom源代码拷贝到主函数中

1. 源代码编译运行，编译运行成功，说明成功配置glut库，可以正常运行

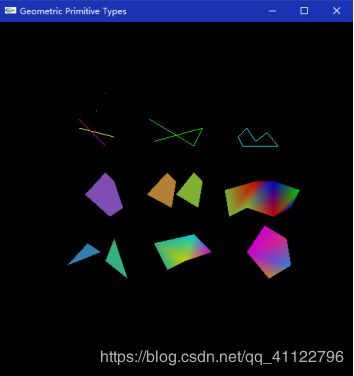
运行结果如下

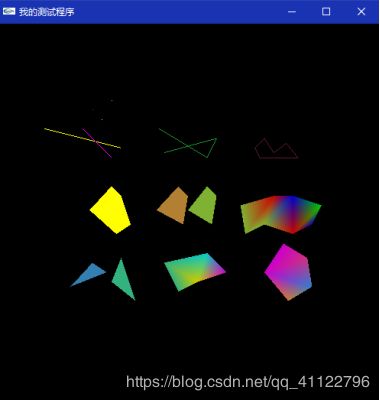
1. 改变标题栏和图形坐标、颜色等参数，运行结果如下

1. 其中黄色线段被拉长，对应语句为

glVertex2f(-15.0,9.0); //原为glVertex2f(-11.0,8.0);

1. 开折线颜色变浅，对应语句为

glColor3f(0.1,0.6,0.2); //原为glColor3f(0.0,1.0,0.0);

1. 闭折线颜色变为红色，对应语句为

glColor3f(1.0,0.0,0.0); //原为glColor3f(0.0,1.0,1.0);

1. 第一个多边形颜色变为黄色，对应语句为

glColor3f(1,0.1,0.0); //原为glColor3f(0.5,0.3,0.7);

1. 标题栏变为“我的测试程序”，对应语句为

glutCreateWindow("我的测试程序");

//原为glutCreateWindow("Geometric Primitive Types");

1.中点线算法

1.基本原理

1.1直线的一般式

由解析几何，平面上直线L的一般式为

若已知直线上两个点

则有

不妨取

则c为

由此知，可以由任意两点的坐标确定一条直线的一般式。

1.2平面上点与直线的位置关系

由解析几何，平面上任意一点O(m,n)与直线的位置关系有3种，利用直线的一般式，若令

当b>0时，有下面三种情况

由此知，要判断点O与直线L的位置关系时，只需要判断d(x,y)的符号即可，而与d(x,y)的大小无关。

 

2.绘制像素点的算法描述

此时已知直线段的两个端点，需采用中点线算法确定直线，需分类讨论，以斜率取值不同共有四种情况（直线与坐标轴平行的情况除外）。

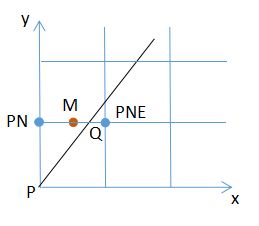
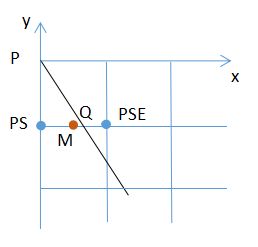
2.1 0

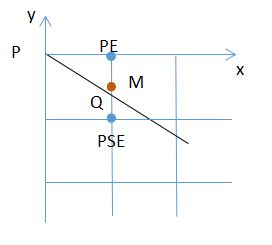
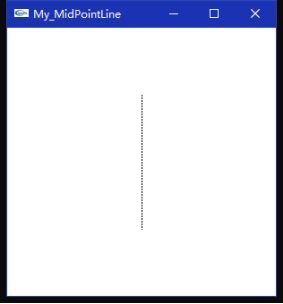
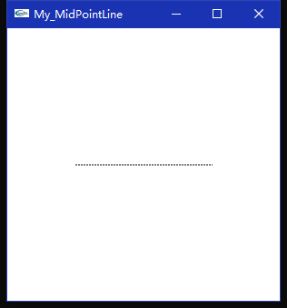
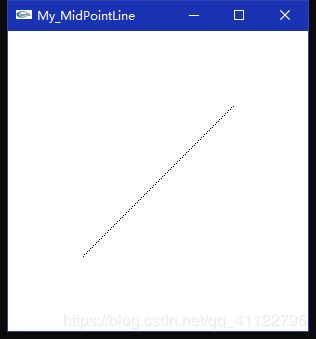
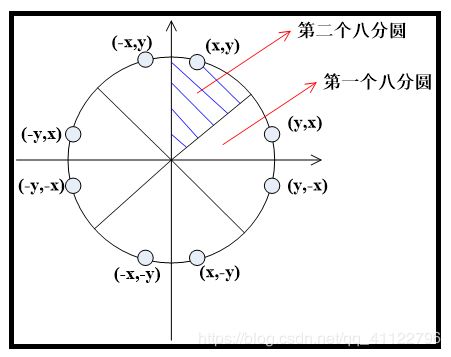
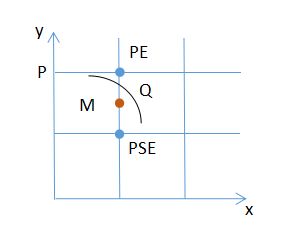
如图，不妨设当前点为P(xp,yp)，由于0

将M点坐标带入直线的一般式，有

d0 = d(xp+1,yp+0.5) = a+0.5b

上式利用了点P在直线L上这一事实。

现对d0的正负号进行讨论

1.若d0>=0

此时直线与线段PEM有交点或经过M，点亮PE象素，且执行

xp=xp+1

yp=yp

下次象素点亮判断d1的符号，d1=d0+a

2.若d0<0

此时直线与线段MPNE有交点且不经过M，点亮PNE象素，且执行

xp=xp+1

yp=yp+1

下次象素点亮判断d1的符号，d1=d0+a+b

重复以上操作，直至xp=x1（这里x1>x0），即可点亮整条直线。

 

2.2 K>1

此时，象素在y方向是致密的，即y每增1，都需要点亮一个象素。依然以M和直线L的位置关系来判断下一个要点亮的象素

为PN还是PNE，其中M的坐标为

M（xp+0.5,yp+1）

 

同理，将M点坐标带入直线的一般式，有

d0 = d(xp+0.5,yp+1) = 0.5a+b

上式利用了点P在直线L上这一事实。

现对d0的正负号进行讨论

1.若d0>0

此时直线与线段MPNE有交点且不经过M，点亮PNE象素，且执行

xp=xp+1

yp=yp+1

下次象素点亮判断d1的符号，d1=d0+a+b

2.若d0<=0

此时直线与线段PNM有交点或经过M，点亮PN象素，且执行

xp=xp

yp=yp+1

下次象素点亮判断d1的符号，d1=d0+b

重复以上操作，直至yp=y1（这里y1>y0），即可点亮整条直线。

 

2.3 -1<=K<0

此时象素在x方向是致密的，即x每增1，都需要点亮一个象素。依然以M和直线L的位置关系来判断下一个要点亮的象素为PE还是PSE，其中M的坐标为

M（xp+1,yp-0.5）

 

同理，将M点坐标带入直线的一般式，有

d0 = d(xp+1,yp-0.5) = a-0.5b

上式利用了点P在直线L上这一事实。

现对d0的正负号进行讨论

1.若d0>=0

此时直线与线段PSEM有交点或经过M，点亮PSE象素，且执行

xp=xp+1

yp=yp-1

下次象素点亮判断d1的符号，d1=d0+a-b

2.若d0<0

此时直线与线段MPE有交点且不经过M，点亮PE象素，且执行

xp=xp+1

yp=yp

下次象素点亮判断d1的符号，d1=d0+a

重复以上操作，直至xp=x1（这里x1>x0），即可点亮整条直线。

 

2.4 K<-1

此时，象素在y方向是致密的，即y每增1，都需要点亮一个象素。依然以M和直线L的位置关系来判断下一个要点亮的象素为PS还是PSE，其中M的坐标为

M（xp+0.5,yp-1）

 

同理，将M点坐标带入直线的一般式，有

d0 = d(xp+0.5,yp-1) = 0.5a-b

上式利用了点P在直线L上这一事实。

现对d0的正负号进行讨论

1. 若d0>0

此时直线与线段MPS有交点且不经过M，点亮PS象素，且执行

xp=xp

yp=yp-1

下次象素点亮判断d1的符号，d1=d0-b

(ii) 若d0<=0

此时直线与线段MPSE有交点或经过M，点亮PSE象素，且执行

xp=xp+1

yp=yp-1

下次象素点亮判断d1的符号，d1=d0+a-b

重复以上操作，直至yp=y0（这里y1>y0），即可点亮整条直线。

 

 

综上，以上四种情况为直线不与坐标轴平行的情况，当直线与坐标轴平行时，依次沿x方向或y方向点亮直线即可，即一共有六种情况。

 

3.运行结果

1.点的坐标为（-50,0）（50,0）与y轴平行

2.点的坐标为（0,-50）（0,50）与x轴平行

 

3.点的坐标为（-50,-50）（50,50）斜率为1

 

 

4.点的坐标为（-20,-50）（20,50）斜率为2.5

 

 

5.点的坐标为（-50,50）（50,50）斜率为-1

 

6.点的坐标为（-20,50）（20,-50）斜率为-2.5

 

源代码见附录

2.中点圆算法

1.基本原理

1.1平面上点与圆的位置关系

设圆O的方程为

则平面上任意一点M（m，n）与圆O的位置关系有下面三种情况

由此知，要判断点M与圆O的位置关系时，只需要判断F(M)的符号即可，而与F(M)的大小无关。

 

2.算法描述

2.1圆的八方对称性

 

由上图知，只要描述出一个八分圆的算法实现，

如

WritePixel (x, y, r);

则可以通过对称性来获得整个圆的象素点绘制

如

void CirclePoints (int x,int y,int r)

{

WritePixel (x, y, r);

WritePixel (y, x, r);

WritePixel (y, -x, r);

WritePixel (x, -y, r);

WritePixel (-x, -y, r);

WritePixel (-y, -x, r);

WritePixel (-y, x, r);

WritePixel (-x, y, r);

}

 

2.2一个八分圆的算法实现

如图，可以取第二个八分圆，第二个八分圆在x方向上是致密的。即x每增1，都需要点亮一个象素。以M和圆的位置关系来判断下一个要点亮的象素为PE还是PSE，其中M的坐标为

M（xp+1,yp-0.5）

 

将M点坐标带入F(M)，有

d0 = F(xp+1,yp-0.5) = 2xp-yp+1.25

上式利用了点P在圆上这一事实。

现对d0的正负号进行讨论

（i）若d0>=0

此时圆与线段PSEM有交点或经过M，点亮PSE象素，且执行

d1=d0+2xp-2yp+5

xp=xp+1

yp=yp-1

下次象素点亮判断d1的符号。

（ii）若d0<0

此时直线与线段MPE有交点且不经过M，点亮PE象素，且执行

d1=d0+2xp+3

xp=xp+1

yp=yp

下次象素点亮判断d1的符号。

重复以上操作，直至（这里x0=0），即可点亮第二个八分之一圆。

综上，通过一个八分之一圆的绘制以及圆的八分对称性即可绘制整个圆。

 

3.运行结果

我把点宽调成了2，然后多次调用中点圆函数，绘制了一个奥运五环。

 

四、实验心得

说实话，第一次用比较底层的c语言写出图形窗口界面还是挺激动的。中间经历了许多挫折，如配置出错啊、各种bug啊，不过最终还是成功地利用OpenGL写出了中点线算法。最大的感受是一切问题都是纸老虎，都可以通过老师同学或者网络解决。当然非常开心的一点是弄清楚了直线的栅格显示问题，我觉得自己做的最重要的一步就是在报告中对中点线算法原理进行了细致的分析，即进行了很详细的数学建模，最后用代码实现了这个数学模型，并验证了该模型的正确性。

说到底，任何问题的第一步也是最难的一步就是建模，而对于理工科的学生而言，建模肯定不是用自然语言建模，一定是用详细明确的数学语言来建模，即数学建模。之后就是怎么实现了，但是代码实现说到底都是小问题，什么glut库的配置啊，语法啊，一些小bug啊。最重要的是要有建模思想和算法思想，我认为这是我本次实验最大的收获。

 

 

附录：程序源代码

1. 简单图元绘制

#include "windows.h"

#include

void myinit()

{

glClearColor(0.0,0.0,0.0,0.0);

 

}

 

void ChangeSize(GLsizei w,GLsizei h)

{

glViewport(0,0,w,h);

glMatrixMode(GL_PROJECTION);

glLoadIdentity();

 

if(w<=h)

glOrtho(-20.0,20.0,-20.0*(GLfloat)h/(GLfloat)w,20.0*(GLfloat)h/(GLfloat)w,-50.0,50.0);

else

glOrtho(-20.0*(GLfloat)h/(GLfloat)w,20.0*(GLfloat)h/(GLfloat)w,-20.0,20.0,-50.0,50.0);

glMatrixMode(GL_MODELVIEW);

glLoadIdentity();

}

void DrawMyObjects()

{

 

//画点

glBegin(GL_POINTS);

glColor3f(1.0,0.0,0.0);

glVertex2f(-10.0,11.0);

glColor3f(1.0,1.0,0.0);

glVertex2f(-9.0,10.0);

glColor3f(0.0,1.0,1.0);

glVertex2f(-8.0,12.0);

glEnd();

//画线段

glBegin(GL_LINES);

glColor3f(1.0,1.0,0.0);

 

glVertex2f(-15.0,9.0);//原为glVertex2f(-11.0,8.0);

glVertex2f(-7.0,7.0);

glColor3f(1.0,0.0,1.0);

glVertex2f(-11.0,9.0);

glVertex2f(-8.0,6.0);

glEnd();

//画开折线

glBegin(GL_LINE_STRIP);

glColor3f(0.1,0.6,0.2);//

// glPointSize(5);

glVertex2f(-3.0,9.0);

glVertex2f(2.0,6.0);

glVertex2f(3.0,8.0);

glVertex2f(-2.5,6.5);

glEnd();

//画闭折线

glBegin(GL_LINE_LOOP);

glColor3f(0.4,0.1,0.2);//

glVertex2f(7.0,7.0);

glVertex2f(8.0,8.0);

glVertex2f(9.0,6.5);

glVertex2f(10.3,7.5);

glVertex2f(11.5,6.0);

glVertex2f(7.5,6.0);

glEnd();

//画填充多边形

glBegin(GL_POLYGON);

glColor3f(1.0,1.0,0);

glVertex2f(-7.0,2.0);

glVertex2f(-8.0,3.0);

glVertex2f(-10.3,0.5);

glVertex2f(-7.5,-2.0);

glVertex2f(-6.0,-1.0);

glEnd();

//画四边形

glBegin(GL_QUADS);

glColor3f(0.7,0.5,0.2);

glVertex2f(0.0,2.0);

glVertex2f(-1.0,3.0);

glVertex2f(-3.3,0.5);

glVertex2f(-0.5,-1.0);

glColor3f(0.5,0.7,0.2);

glVertex2f(3.0,2.0);

glVertex2f(2.0,3.0);

glVertex2f(0.0,0.5);

glVertex2f(2.5,-1.0);

glEnd();

//画连接四边形

glBegin(GL_QUAD_STRIP);

glVertex2f(6.0,-2.0);

glVertex2f(5.5,1.0);

glVertex2f(8.0,-1.0);

glColor3f(0.8,0.0,0.0);

glVertex2f(9.0,2.0);

glVertex2f(11.0,-2.0);

glColor3f(0.0,0.0,0.8);

glVertex2f(11.0,2.0);

glVertex2f(13.0,-1.0);

glColor3f(0.0,0.8,0.0);

glVertex2f(14.0,1.0);

glEnd();

//画三角形

glBegin(GL_TRIANGLES);

glColor3f(0.2,0.5,0.7);

glVertex2f(-10.0,-5.0);

glVertex2f(-12.3,-7.5);

glVertex2f(-8.5,-6.0);

glColor3f(0.2,0.7,0.5);

glVertex2f(-8.0,-7.0);

glVertex2f(-7.0,-4.5);

glVertex2f(-5.5,-9.0);

glEnd();

//画连续三角形

glBegin(GL_TRIANGLE_STRIP);

glVertex2f(-1.0,-8.0);

glVertex2f(-2.5,-5.0);

glColor3f(0.8,0.8,0.0);

glVertex2f(1.0,-7.0);

glColor3f(0.0,0.8,0.8);

glVertex2f(2.0,-4.0);

glColor3f(0.8,0.0,0.8);

glVertex2f(4.0,-6.0);

glEnd();

//画扇形三角形

glBegin(GL_TRIANGLE_FAN);

glVertex2f(8.0,-6.0);

glVertex2f(10.0,-3.0);

glColor3f(0.8,0.2,0.5);

glVertex2f(12.5,-4.5);

glColor3f(0.2,0.5,0.8);

glVertex2f(13.0,-7.5);

glColor3f(0.8,0.5,0.2);

glVertex2f(10.5,-9.0);

glEnd();

}

void RenderScene()

{

glClear(GL_COLOR_BUFFER_BIT);

glColor3f(1.0,1.0,0.0);

DrawMyObjects();

glFlush();

}

int main()

{

glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB);

glutInitWindowSize(500,500);

glutInitWindowPosition(0,0);

 

glutCreateWindow("我的测试程序");

 

myinit();

glutDisplayFunc(RenderScene);

glutReshapeFunc(ChangeSize);

 

glutMainLoop();

return 0;

}

 

1. 中点线算法

#include "windows.h"

#include

#include

#include

typedef struct {

int x,y;

}point;

void init()

{

glClearColor(1.0f,1.0f,1.0f,1.0f);

    //glMatrixMode(GL_PROJECTION);

//gluOrtho2D(-250.0, 250.0, -250.0, 250.0);

}

int LineMidPoint(int x0,int y0,int x1,int y1,point pixels[])

{

    using namespace std;

int num,x,y,dx,dy;

int a,b,d;

float k;

dx = x1-x0;

dy = y1-y0;

//cout<<"dy is "<

    //    <<"dx is "<

if(dy == 0)

        k=dx;

    else

        k = (float)dy/dx;

num = 0;

/*cout<<"k is "<

        <<"x0 is "<

        <<"x1 is "<

        <<"y0 is "<

        <<"y1 is "<

        <<"k should be"<

if(dx>0)

    {

        a=-dy;

        b=dx;

    }

    else

    {

        a=dy;

        b=-dx;

    }

 

if(dx==0) //垂直线

{

for(y=y0;y<=y1;y++)

{

pixels[num].x = x0;

pixels[num].y = y;

num ++;

}

 

}

else if(dy==0) //水平线

{

for(x=x0;x<=x1;x++)

{

pixels[num].x = x;

pixels[num].y = y0;

num ++;

}

}

else if(k<=1&&k>0)//斜率的四种情况

{

    x = x0;

y = y0;

d = 2*a+b;

pixels[num].x = x0;

        pixels[num].y = y0;

        num ++;

for(x=x0;x

{

 

    if(d>=0){

                pixels[num].x = x+1;

                pixels[num].y = y;

                num ++;

 

                d+=2*a;

    }

else

            {

                pixels[num].x = x+1;

                pixels[num].y = y+1;

                num ++;

                //cout<<"I'm here "<

                y++;

                d+=2*a+2*b;

            }

 

}

}

else if(k>1)

{

x = x0;

y = y0;

d = a+2*b;

pixels[num].x = x0;

        pixels[num].y = y0;

        num ++;

for(y=y0;y

{

 

    if(d>0){

                pixels[num].x = x+1;

                pixels[num].y = y+1;

                num ++;

                x++;

 

                d+=2*a+2*b;

    }

else

            {

                pixels[num].x = x;

                pixels[num].y = y+1;

                num ++;

 

 

                d+=2*b;

            }

 

}

}

    else if(k<0&&k>=-1)

{

    x = x0;

y = y0;

d = 2*a-b;

pixels[num].x = x0;

        pixels[num].y = y0;

        num ++;

for(x=x0;x

{

 

    if(d>=0){

                pixels[num].x = x+1;

                pixels[num].y = y-1;

                num ++;

 

                y--;

                d+=2*a-2*b;

    }

else

            {

                pixels[num].x = x+1;

                pixels[num].y = y;

                num ++;

 

 

                d+=2*a;

            }

 

}

}

else

    {

        x = x0;

y = y0;

d = a-2*b;

pixels[num].x = x0;

        pixels[num].y = y0;

        num ++;

for(y=y0;y>y1;y--)

{

 

    if(d>0){

                pixels[num].x = x;

                pixels[num].y = y-1;

                num ++;

 

 

                d-=2*b;

    }

else

            {

                pixels[num].x = x+1;

                pixels[num].y = y-1;

                num ++;

                x++;

 

                d+=2*a-2*b;

            }

 

}

    }

return num;

}

 

 

 

void drawLine(int x1,int y1,int x2,int y2)

{

point pixels[1000];

int num;

int i;

num = LineMidPoint(x1,y1,x2,y2,pixels);

glBegin(GL_POINTS);

for(i=0;i

glVertex2d(pixels[i].x,pixels[i].y);

glEnd();

}

 

 

 

void RenderScene()

{

glClear(GL_COLOR_BUFFER_BIT);

glColor3f(0.0f,0.0f,0.f);

drawLine(0,-50,0,50);//两个点的坐标

glFlush();

}

 

void ChangeSize(GLsizei w,GLsizei h)

{

GLfloat aspectRatio;

if(h==0)

h = 1;

glViewport(0,0,w,h);

glMatrixMode(GL_PROJECTION);

glLoadIdentity();

 

aspectRatio = (GLfloat)w/(GLfloat)h;

if(w<=h)

glOrtho(-100.0,100.0,-100.0/aspectRatio,100.0/aspectRatio,1.0,-1.0);

else

glOrtho(-100.0*aspectRatio,100.0*aspectRatio,-100.0,100.0,1.0,-1.0);

 

glMatrixMode(GL_MODELVIEW);

glLoadIdentity();

}

 

int main()

{

 

glutInitDisplayMode(GLUT_RGB|GLUT_SINGLE);

glutCreateWindow("My_MidPointLine");

 

init();

 

glutDisplayFunc(RenderScene);

glutReshapeFunc(ChangeSize);

 

glutMainLoop();

return 0;

}

 

3.中点圆算法

#include "windows.h"

#include

#include

#include

typedef struct {

int x,y;

}point;

void init()

{

glClearColor(1.0f,1.0f,1.0f,1.0f);

    //glMatrixMode(GL_PROJECTION);

//gluOrtho2D(-250.0, 250.0, -250.0, 250.0);

}

 

int WritePixel (int xp, int yp, int r,point pixels[],int num)

{

    float d = 2*xp-yp+1.25;

    for(;xp<=r*sqrt(2)/2;xp++)

    {

        if(d>=0)

        {

            d+=2*xp-2*yp+5;

            pixels[num].x=xp+1;

            pixels[num].y=yp-1;

 

            yp=yp-1;

            num++;

        }

        else

        {

            d+=2*xp+3;

            pixels[num].x=xp+1;

            pixels[num].y=yp;

            num++;

 

        }

    }

    return num;

 

 

}

 

int CircleMidPoint(int x0,int y0,int r,point pixels[])

{

    using namespace std;

int num,i,n;

int xp,yp;

 

num = 0;

xp=0;

yp=r;

num=WritePixel(xp,yp,r,pixels,num);

n=num;

//cout<<"num1="<

for(i=1;i<=n;i++)

    {

        pixels[num].x=pixels[n-i].y;//第一个八分圆和第二个八分圆关于y=x对称

        pixels[num].y=pixels[n-i].x;

        num++;

    }

    n=num;

    //cout<<"num2="<

for(i=1;i<=n;i++)

    {

        pixels[num].x=pixels[n-i].x;//第一象限和第二象限圆关于y=0对称

        pixels[num].y=-pixels[n-i].y;

        num++;

    }

n=num;

//cout<<"num3="<

for(i=1;i<=n;i++)

    {

        pixels[num].x=-pixels[n-i].x;//右半圆和左半圆关于x=0对称

        pixels[num].y=pixels[n-i].y;

        num++;

    }

n=num;

//cout<<"num4="<

for(i=0;i

    {

        pixels[i].x+=x0;//圆的整体平移

        pixels[i].y+=y0;

 

    }

 

return num;

}

 

 

 

 

 

 

 

 

 

void drawCircle(int x1,int y1,int r)

{

point pixels[1000];

int num;

int i;

num = CircleMidPoint(x1,y1,r,pixels);

glPointSize(2);

glBegin(GL_POINTS);

for(i=0;i

glVertex2d(pixels[i].x,pixels[i].y);

glEnd();

}

 

 

 

void RenderScene()

{

glClear(GL_COLOR_BUFFER_BIT);

glColor3f(0.0f,0.0f,0.f);

drawCircle(0,20,20);//圆心的坐标和半径

glColor3f(0.0f,0.0f,1.f);

drawCircle(-40,20,20);//圆心的坐标和半径

glColor3f(1.0f,0.0f,0.f);

drawCircle(40,20,20);//圆心的坐标和半径

glColor3f(1.0f,1.0f,0.0f);

drawCircle(-20,-16,20);//圆心的坐标和半径

glColor3f(0.0f,1.0f,0.f);

drawCircle(20,-16,20);//圆心的坐标和半径

glFlush();

}

 

void ChangeSize(GLsizei w,GLsizei h)

{

GLfloat aspectRatio;

if(h==0)

h = 1;

glViewport(0,0,w,h);

glMatrixMode(GL_PROJECTION);

glLoadIdentity();

 

aspectRatio = (GLfloat)w/(GLfloat)h;

if(w<=h)

glOrtho(-100.0,100.0,-100.0/aspectRatio,100.0/aspectRatio,1.0,-1.0);

else

glOrtho(-100.0*aspectRatio,100.0*aspectRatio,-100.0,100.0,1.0,-1.0);

 

glMatrixMode(GL_MODELVIEW);

glLoadIdentity();

}

 

int main()

{

 

glutInitDisplayMode(GLUT_RGB|GLUT_SINGLE);

glutCreateWindow("My_MidPointCircle");

 

init();

 

glutDisplayFunc(RenderScene);

glutReshapeFunc(ChangeSize);

 

glutMainLoop();

return 0;

}