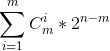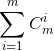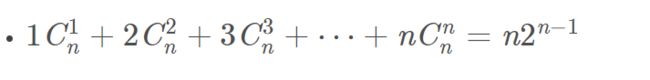暨武汉大学2020年大学生程序设计大赛决赛(重现赛)(A,D(推公式),F,G(暴力模拟)H,I(二分+分块) J(OEIS or 卡特兰数))
题目链接
比较菜只A出了五题
A-A Simple Problem about election
题意:现在有n个人必须投m张票给别人,且最多给同一个人一张票,现在 ZZZZSGW 是最后一个投票的,且他已经知道了n个人目前获得票数的情况,问ZZZZSGW 最高的排名是多少,票数越高的排在前面
做法:自己肯定给自己投一票,然后 优先给小于 ZZZZSGW 和大于 ZZZZSGW的投票 剩下再考虑给跟ZZZZSGW 一样票的投
这题卡常,索性写在一个for循环里 看你咋卡我
#include
#define rep(i,a,b) for(int i=a;i<=(b);++i)
#define per(i,a,b) for(int i=a;i>=(b);--i)
#define mem(a,x) memset(a,x,sizeof(a))
#define pb push_back
#define pi pair
#define mk make_pair
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b) { return b?gcd(b,a%b):a;}
const int N=1e5+10;
int n,m,a[N],x[N],len;
void solve()
{
scanf("%d%d",&n,&m);
int tot=0,sum=0,ans=1;
rep(i,1,n) {
scanf("%d",&a[i]);
if(i==1) continue;
if(a[i]==a[1]) tot++; else sum++;
if(a[i]>a[1]) ans++;
}
m-=sum+1;
if(m>=0) ans+=m;
printf("%d\n",ans);
}
int main()
{
int _;cin>>_;while(_--)
solve();
}
D-Deploy the medical team
题意:现有n个人,n个人中有m个人有资格当队长,现要求你从n个中选一部分凑成一队,每队必须有一个队长,问队伍的方案数。注意 成员不同或者队长不同视为不同的方案数
做法:n 分成两部分:
只能当作成员:n-m 个
能当队长和成员:m个
更多组合数公式:博客
#include
#define rep(i,a,b) for(int i=a;i<=(b);++i)
#define per(i,a,b) for(int i=a;i>=(b);--i)
#define mem(a,x) memset(a,x,sizeof(a))
#define pb push_back
#define pi pair
#define mk make_pair
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b) { return b?gcd(b,a%b):a;}
const ll mod=1e9+7;
ll powmod(ll a,ll b) {ll res=1;a%=mod;
assert(b>=0); for(;b;b>>=1){if(b&1)res=res*a%mod;a=a*a%mod;}return res;}
void solve()
{
ll n,m;
scanf("%lld%lld",&n,&m);
if(m==0){
puts("0");
return ;
}
n-=m;
ll ans=powmod(2,n)*m%mod*powmod(2,m-1)%mod;
printf("%lld\n",ans);
}
int main()
{
int _;cin>>_;while(_--)
solve();
} F-Figure out the sequence
题意:给定两个字符串s 、t , 定义函数:F[i]: F[1]=s F[2]=t F[i]=F[i-2]+F[i-1]
输出i、第n个字符F[i]内各个字符的个数,字符从字典序从大到小排序输出,0个的就不用输出了。
做法:由于n只有40 暴力一下保存各个字符个数就行了,水题。
#include
#define rep(i,a,b) for(int i=a;i<=(b);++i)
#define per(i,a,b) for(int i=a;i>=(b);--i)
#define mem(a,x) memset(a,x,sizeof(a))
#define pb push_back
#define pi pair
#define mk make_pair
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b) { return b?gcd(b,a%b):a;}
const ll mod=1e9+7;
ll powmod(ll a,ll b) {ll res=1;a%=mod;
assert(b>=0); for(;b;b>>=1){if(b&1)res=res*a%mod;a=a*a%mod;}return res;}
const int N=60;
char s[N],t[N];
ll dp[N][N];
int get(char c)
{
if('A'<=c&&c<='Z') return c-'A';
return c-'a'+26;
}
char get1(int i)
{
if(0<=i&&i<=25) return i+'A';
return i-26+'a';
}
void solve()
{
scanf("%s%s",s+1,t+1);
int len=strlen(s+1);
rep(i,1,len) dp[1][get(s[i])]++;
len=strlen(t+1);
rep(i,1,len) dp[2][get(t[i])]++;
int n;
scanf("%d",&n);
for(int i=3;i<=n;++i){
for(int j=0;j<52;++j) dp[i][j]=dp[i-1][j]+dp[i-2][j];
}
for(int i=0;i<52;++i){
if(dp[n][i]){
printf("%c: %d\n",get1(i),dp[n][i]);
}
}
}
int main()
{
//int _;cin>>_;while(_--)
solve();
} G-Game Strategy
题意:Alice Bob 和 Cindy玩游戏,最初每个人有n个数 每轮 每个人去掉一个数(Alice 先,Bob第二 Cindy最后),直到最后每人 剩一个数 计算和sum=x+y+z Alice 想要这个sum尽量大,Bob想要这个sum尽量小,Cindy想要这个sum尽量靠近0
做法:n^3方暴力枚举即可。参考来自:博客 没想到这么妙的做法
#include
using namespace std;
const int N=101;
int a[N],b[N],c[N];int n;
inline int dfs2(int now){
int ans=2e9;
for(int i=1;i<=n;++i){
if(abs(now+c[i])
H-Hinnjaku
这题看起来难,题面有点长,读懂就是水题一个了。
题意:有两个人:JOJO 和 Dio 玩游戏 两个人各自有n长度的字符串,以及相同的血量h
现从1开始遍历字符串,当 JOJO 有连续的后缀字符是ora 那么就会施法使得Dio 血量减一
当Dio有连续的后缀字符是muda 那么就会施法使得JOJO 血量减一
当Dio有连续的后缀字符是zawaluduo 会使得JOJO瞬间没血
当JOJO有连续的后缀字符是zawaluduo 会使得Dio瞬间没血
如果同时发现zawaluduo 优先执行JOJO的。
判断最后谁赢了
做法:模拟一下就可以了。
#include
#define rep(i,a,b) for(int i=a;i<=(b);++i)
#define per(i,a,b) for(int i=a;i>=(b);--i)
#define mem(a,x) memset(a,x,sizeof(a))
#define pb push_back
#define pi pair
#define mk make_pair
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b) { return b?gcd(b,a%b):a;}
const int N=2e4+10;
char s[N],t[N];
int n,h1,h2;
void solve()
{
scanf("%d%d",&n,&h1);
cin>>s+1>>t+1;
h2=h1;
int flag;
string tmp="zawaluduo";
for(int i=3;i<=n&&h1&&h2;++i){
if(i>=9) {
int f=1;
for(int j=0,k=i-8;j<9;++j,++k) if(t[k]!=tmp[j]) f=0;
if(f) {
h1=0;break;
}
f=1;
for(int j=0,k=i-8;j<9;++j,++k) if(s[k]!=tmp[j]) f=0;
if(f) {
h2=0;break;
}
}
if(s[i-2]=='o'&&s[i-1]=='r'&&s[i]=='a') h2--;
if(i<4)continue;
if(t[i-3]=='m'&&t[i-2]=='u'&&t[i-1]=='d'&&t[i]=='a') h1--;
}
if(h1>h2) puts("Wryyyyy");
else if(h2>h1) puts("Hinnjaku");
else puts("Kono Dio da");
}
int main()
{
//ios::sync_with_stdio(false);
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
int _;cin>>_;while(_--)
solve();
} I-Interesting Matrix Problem
重点讲下I题,感觉I题是AC题中比较不错的一个题
题意:给你N *M的矩阵 (1<=N , M <=1e8)矩阵内的值是 i*j 现有q次询问,每次询问输入k 代表 查询这个矩阵内第k小的数是多少。
做法:第一思路二分答案,然后mid去check O(N) 枚举行 i 计算mid/i的个数,发现会超时
这个公式好眼熟啊,不就是数论的整除分块,果断套了一个分块 时间复杂度:q*sqrt(N)
注意还要判断mid/i 和m的大小关系
#include
#define rep(i,a,b) for(int i=a;i<=(b);++i)
#define per(i,a,b) for(int i=a;i>=(b);--i)
#define mem(a,x) memset(a,x,sizeof(a))
#define pb push_back
#define pi pair
#define mk make_pair
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b) { return b?gcd(b,a%b):a;}
ll n,m,q,k;
int valid(ll mid)
{
ll ans=0;
ll l,r;
for(l=1;l<=mid;l=r+1){
r=mid/(mid/l);
ll t=mid/l;
t=min(t,m);
ans+=(1ll*r-l+1)*t;
}
return ans>=k;
}
void solve()
{
scanf("%lld%lld%lld",&n,&m,&q);
if(n>m) swap(n,m);
while(q--){
scanf("%lld",&k);
ll l=1,r=m,ans;
while(l<=r){
ll mid=l+r>>1;
if(valid(mid)) {
ans=mid,r=mid-1;
//printf("midmid:%lld\n",mid);
}
else l=mid+1;
}
printf("%lld\n",ans);
}
}
int main()
{
solve();
} J-Jogging along the Yangtze River
题意:输入n 现在二维平面上,初始点在(0,0) 要走到(2n,0)
走的方案如下:
① (x,y)->(x+2,y)
② (x,y)->(x+1,y+1)
③ (x,y)->(x+1,y-1)
如果没有1操作 就是一个卡特兰数
这里有两种做法,oeis做法或者推卡特兰数+可重集排列数(这个还在补)
百度oeis 输入2,6,22,90
找到formula 这招适合网络赛时候用,现场赛可能就gg了 然而大部分不就是网络赛吗,现场赛不要钱的吗
![]()
公式写在草稿纸上:
![]()
#include
using namespace std;
const int N=1e5+1,mod=998244353;
int C[N],g[N];
int main(){
C[0]=g[0]=g[1]=1;
for(int i=2;i