矩阵分解（MF）算法代码实现

 #迭代退出既控制次数又控制条件如果在迭代过程中能够提前退出就提前退出

参数调整是最大问题

import numpy as np
#迭代退出既控制次数又控制条件如果在迭代过程中能够提前退出就提前退出
def MF(R,P,Q,K,steps,alpha,beta):
    m, n = R.shape
    for step in range(steps):
        for i in range(m):
            for j in range(n):
                if R[i][j]:
                    eij = R[i][j] - np.dot(P[i,:],Q[:,j])#内积运算
                    for k in range(K):
                        P[i][k] += alpha * (2 * eij * Q[k][j] - beta * P[i][k])
                        Q[k][j] += alpha * (2 * eij * P[i][k] - beta * Q[k][j])
        #所有的变量更新一遍之后判断一下损失函数是否满足退出条件
        loss = 0
        for i in range(m):
            for j in range(n):
                if R[i][j]:
                    eij = R[i][j] - np.dot(P[i, :], Q[:, j])
                    loss += pow(eij,2)
                    for k in range(K):
                        loss += (beta / 2) * (pow(P[i][k],2)+pow(Q[k,j],2))
        if loss < 1.1 :
            return P,Q
if __name__ == '__main__':
    R = np.array([ [5, 3, 0, 1],
                   [4, 0, 0, 1],
                   [1, 0, 0, 4],
                   [0, 1, 5, 4],
                   [0, 1, 5, 4]])
    k = 5
    m, n = R.shape
    P = np.random.rand(m,k)#初始化 随便赋值就ok
    Q = np.random.rand(k,n)
    new_P,new_Q = MF(R,P,Q,k,2000000,0.0002,0.02)
    new_R = np.matmul(new_P,new_Q)
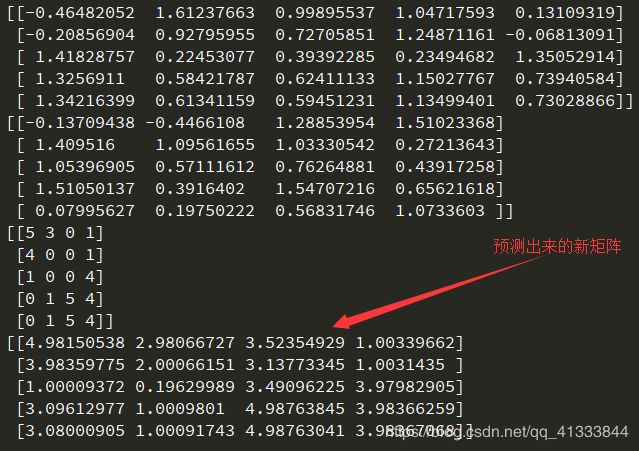
    print(new_P)
    print(new_Q)
    print(R)
    print(new_R)