用梯度下降算法解决线性回归问题
问题引入
假设现在你现在手头上关于房子信息和房价,你朋友给出自己房子信息,叫你帮他预测一下能卖多少钱,房子的信息有房子的大小,卧室的数目。
问题分析
这种给出变量和结果的问题我们可以通过用线性回归的知识来解决。设线性回归方程为
h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 h_\theta(x) = \theta_0+\theta_1x_1+\theta_2x_2 hθ(x)=θ0+θ1x1+θ2x2
向量 x x x表示的是房子的信息,向量 θ \theta θ表示的是特征值,我们可以通过设置向量 θ \theta θ的值来确定出一个与实际值相差不大的回归方程,然后通过将我们所要估计的房子信息带入到 h θ ( x ) h_\theta(x) hθ(x)中求得估计结果。
那么我们通过什么方式来求得比较合适的特征向量值呢,下面就要用到我们所说的梯度下降算法了。
梯度下降
在引入梯度下降算法之前,我们需要对特征向量 θ \theta θ是否合适设置一个衡量标准,想一想,我们通过设置的特征向量 θ \theta θ带入实际真实数据得出 h ( x ) h(x) h(x)与实际正确的y比对,肯定是越接近y越好,也就是误差越小越好,所以我们可以通过代价函数来进行判定向量 θ \theta θ,这里我们设置代价函数为:
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta) = \frac{1}{2m}\sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})^2 J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2
这里的 x ( i ) x^{(i)} x(i) 和 y ( i ) y^{(i)} y(i)分别表示第i组房子信息的值和房价
举个例子:
x ( i ) = [ x 1 ( i ) x 2 ( i ) ] x^{(i)} =\begin{bmatrix} x_1^{(i)} \\ x_2^{(i)} \end{bmatrix} x(i)=[x1(i)x2(i)]
y ( i ) y^{(i)} y(i) 就是第i组房价。为了方便之后的矩阵运算,我们在 x x x向量中加入 x 0 x_0 x0,让它恒等于1
这样 x ( i ) x^{(i)} x(i)就变成了下面这种形式:
x ( i ) = [ x 0 ( i ) = 1 x 1 ( i ) x 2 ( i ) ] x^{(i)} =\begin{bmatrix} x_0^{(i)} =1 \\ x_1^{(i)} \\ x_2^{(i)} \end{bmatrix} x(i)=⎣⎢⎡x0(i)=1x1(i)x2(i)⎦⎥⎤
回到上面的内容,那么我们如何调整成合适的 θ \theta θ向量呢,这就用到了我们的梯度下降算法。
通过对 J ( θ ) J(\theta) J(θ) 求每一个 θ i \theta_i θi的偏导 ∂ ∂ θ i J ( θ ) \frac{\partial}{\partial{\theta_i}}J(\theta) ∂θi∂J(θ),然后乘上一个合适的学习速率 α \alpha α,用每一个 θ i \theta_i θi减去 α ∂ ∂ θ i J ( θ ) \alpha\frac{\partial}{\partial{\theta_i}}J(\theta) α∂θi∂J(θ),即:
θ i = θ i − α ∂ ∂ θ i J ( θ ) \theta_i = \theta_i - \alpha\frac{\partial}{\partial{\theta_i}}J(\theta) θi=θi−α∂θi∂J(θ)
这样通过对训练数据的不断迭代,求出最小的 J ( θ ) J(\theta) J(θ),之后通过 h ( θ ) h(\theta) h(θ)估计出结果。
算法实现
这里引用的是吴恩达老师的机器学习的第二周作业中的数据集。
使用的编辑器是Octave
数据集截图:
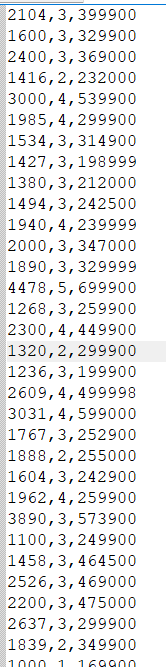
第一和第二列表示的是房子信息,第三列表示的是房价
读入数据
data = load('ex1data2.txt');
X = data(:, 1:2);
y = data(:, 3);
X表示房子信息所有的数据集,y表示的是房价数据集
也就是:
X = [ x ( 0 ) T x ( 1 ) T x ( 2 ) T . . . x ( m ) T ] X = \begin{bmatrix} {x^{(0)}}^T \\ {x^{(1)}}^T \\ {x^{(2)}}^T \\ {...} \\ {x^{(m)}}^T \end{bmatrix} X=⎣⎢⎢⎢⎢⎢⎢⎡x(0)Tx(1)Tx(2)T...x(m)T⎦⎥⎥⎥⎥⎥⎥⎤
y = [ y ( 0 ) y ( 1 ) y ( 2 ) . . . y ( m ) ] y = \begin{bmatrix} y^{(0)} \\ y^{(1)} \\ y^{(2)} \\ {...}\\ y^{(m)} \end{bmatrix} y=⎣⎢⎢⎢⎢⎡y(0)y(1)y(2)...y(m)⎦⎥⎥⎥⎥⎤
这里m表示数据组数
特征缩放
由于第一个特征值与第二个特征值存在指数级的差距,会导致预测不准确,我们需要对特征值进行缩放,缩放公式为:
x i = x i − u i s i x_i = \frac {x_i-u_i}{s_i} xi=sixi−ui
其中 u i u_i ui表示的是所有数据中指定特征值的平均值, s i s_i si 表示的是所有数据中指定特征值的标准差
在这里通过一个函数来实现特征缩放:
function [X_norm, mu, sigma] = featureNormalize(X)
% 要返回的缩放后的矩阵
X_norm = X;
% 求平均值
mu = zeros(1, size(X, 2));
% 求标准差
sigma = zeros(1, size(X, 2));
mu = mean(X);
n = size(X,2);
sigma = std(X);
for i=1:n
X_norm(:,i)=(X_norm(:,i)-mu(i))/sigma(i);
endfor
end
代价函数
接下来,我们实现求代价函数的操作
代价函数也是通过一个函数实现
转化成矩阵运算就是:
J ( θ ) = 1 2 m ( X ∗ θ − y ) T ∗ ( X ∗ θ − y ) J(\theta)= \frac{1}{2m}{(X*\theta-y)}^T*(X*\theta-y) J(θ)=2m1(X∗θ−y)T∗(X∗θ−y)
求代价函数代码如下:
function J = computeCostMulti(X, y, theta)
m = length(y); % number of training examples
J = 0;
% 求h(x)
h = X*theta;
loss = (h-y).^2;
J = 1/(2*m)*(X*theta-y)'*(X*theta-y);
end
梯度下降
之后就是梯度下降方法
通过每一次迭代来更新向量 θ \theta θ的值,之后求出代价函数,然后绘出迭代次数与代价函数的2D图像,调整设置的学习速率 α \alpha α使图像稳步下降,直到收敛
代码如下:
function [theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters)
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
for iter = 1:num_iters
m = length(y);
h = X*theta;
loss = h-y;
theta = theta - alpha*(1/m)*(X'*loss);
J_history(iter) = computeCostMulti(X, y, theta);
end
end
绘制代价函数变化图像
通过记录每一次迭代算出的代价函数 J ( θ ) J(\theta) J(θ)来绘制图像
plot(1:numel(J_history), J_history, '-b', 'LineWidth', 2);
xlabel('Number of iterations');
ylabel('Cost J');
