仿射密码解析与实例
仿射密码
原理
仿射密码的加密函数是 E(x)=(ax+b)(modm)
,其中
- x表示明文按照某种编码得到的数字
- a和 m互质
- m是编码系统中字母的数目。
解密函数是 D(x)=a−1(x−b)(modm)
,其中 a−1 是 a 在 Zm
群的乘法逆元。
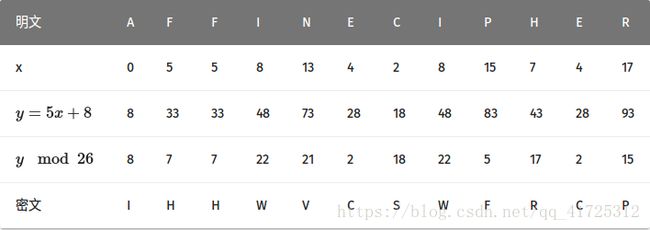
下面我们以 E(x)=(5x+8)mod26
函数为例子进行介绍,加密字符串为 AFFINE CIPHER,这里我们直接采用字母表26个字母作为编码系统
其对应的加密结果是 IHHWVCSWFRCP。
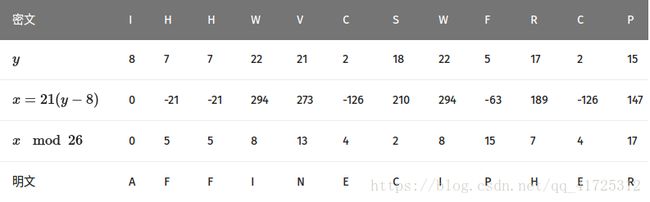
对于解密过程,正常解密者具有a与b,可以计算得到 a−1为 21,
所以其解密函数是D(x)=21(x−8)(mod26)
,解密如下
可以看出其特点在于只有 26 个英文字母。
破解
首先,我们可以看到的是,仿射密码对于任意两个不同的字母,其最后得到的密文必然不一样,所以其也具有最通用的特点。当密文长度足够长时,我们可以使用频率分析的方法来解决。
其次,我们可以考虑如何攻击该密码。可以看出当a=1
时,仿射加密是凯撒加密。而一般来说,我们利用仿射密码时,其字符集都用的是字母表,一般只有26个字母,而不大于26的与26互素的个数一共有
ϕ(26)=ϕ(2)×ϕ(13)=12
算上b的偏移可能,一共有可能的密钥空间大小也就是
12×26=312
一般来说,对于该种密码,我们至少得是在已知部分明文的情况下才可以攻击。下面进行简单的分析。
这种密码由两种参数来控制,如果我们知道其中任意一个参数,那我们便可以很容易地快速枚举另外一个参数得到答案。
但是,假设我们已经知道采用的字母集,这里假设为26个字母,我们还有另外一种解密方式,我们只需要知道两个加密后的字母 y1,y2
即可进行解密。那么我们还可以知道
y1=(ax1+b)(mod26)y2=(ax2+b)(mod26)
两式相减,可得
y1−y2=a(x1−x2)(mod26)
这里 y1,y2
已知,如果我们知道密文对应的两个不一样的字符 x1 与 x2 ,那么我们就可以很容易得到 a ,进而就可以得到 b 了。
例子
这里我们以TWCTF 2016 的 super_express为例进行介绍。简单看一下给的源码
import sys
key = '****CENSORED***************'
flag = 'TWCTF{*******CENSORED********}'
if len(key) % 2 == 1:
print("Key Length Error")
sys.exit(1)
n = len(key) / 2
encrypted = ''
for c in flag:
c = ord(c)
for a, b in zip(key[0:n], key[n:2*n]):
c = (ord(a) * c + ord(b)) % 251
encrypted += '%02x' % c
print encrypted可以发现,虽然对于 flag 中的每个字母都加密了 n 次,如果我们仔细分析的话,我们可以发现
c1=a1c+b1c2=a2c1+b2=a1a2c+a2b1c+b2=kc+d
根据第二行的推导,我们可以得到其实 cn
也是这样的形式,可以看成 cn=xc+y
,并且,我们可以知道的是,key 是始终不变化的,所以说,其实这个就是仿射密码。
此外,题目中还给出了密文以及部分部分密文对应的明文,那么我们就很容易利用已知明文攻击的方法来攻击了,利用代码如下
import gmpy
key = '****CENSORED****************'
flag = 'TWCTF{*******CENSORED********}'
f = open('encrypted', 'r')
data = f.read().strip('\n')
encrypted = [int(data[i:i + 2], 16) for i in range(0, len(data), 2)]
plaindelta = ord(flag[1]) - ord(flag[0])
cipherdalte = encrypted[1] - encrypted[0]
a = gmpy.invert(plaindelta, 251) * cipherdalte % 251
b = (encrypted[0] - a * ord(flag[0])) % 251
a_inv = gmpy.invert(a, 251)
result = ""
for c in encrypted:
result += chr((c - b) * a_inv % 251)
print result结果如下:
➜ TWCTF2016-super_express git:(master) ✗ python exploit.py
TWCTF{Faster_Than_Shinkansen!}