【GCN】论文笔记:SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS
本文为论文SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS的阅读笔记.
github链接:Graph Convolutional Networks
文章目录
- SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS
- 基于图卷积网络的半监督分类
- 摘要
- 1 INTRODUCTION
- 2 Graph中的快速卷积
- 2.1 谱图卷积
- 第一种卷积
- 改进:第二种卷积
- 2.2 线性模型
- K=1:2个参数的模型
- 简化:1个参数的模型
- 推广:特征映射公式
- 3 半监督节点分类
- 3.1 例子
- 预处理操作
- 交叉熵误差
- 训练
- 3.2 实现
- 5 实验
- 5.1 数据集
- 5.2 实验参数
- 1、引文网络数据集
- 2、随机图数据集
- 6 结果
- 6.1 半监督节点分类
- 【参考博文】
SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS
基于图卷积网络的半监督分类
摘要
- 通过谱图卷积(spectral graph convolutions) 的局部一阶近似,来确定卷积网络结构。
- 该模型在图的边数上线性缩放
- 该模型学习隐藏层表示,这些表示既编码局部图结构、也编码节点特征
- 通过图结构数据中部分有标签的节点数据对卷积神经网络结构模型训练,使网络模型对其余无标签的数据进行进一步分类
1 INTRODUCTION
使用神经网络模型 f ( X , A ) f(X,A) f(X,A) 对所有带标签节点进行基于监督损失的训练。
- X X X为输入数据
- A A A为图的邻接矩阵
在图的邻接矩阵上调整 f ( ⋅ ) f(\cdot) f(⋅) 将允许模型从监督损失 L 0 L_0 L0中分配梯度信息,并使其能够学习所有节点(带标签或不带标签)的表示。
2 Graph中的快速卷积
具有以下分层传播规则的多层图形卷积网络(GCN):
(1) H ( l + 1 ) = σ ( D ~ − 1 2 A ~ D ~ − 1 2 H ( l ) W ( l ) ) H^{(l+1)}=\sigma(\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} H^{(l)} W^{(l)}) \tag{1} H(l+1)=σ(D~−21A~D~−21H(l)W(l))(1)
其中:
- A ~ = A + I N \tilde{A}=A+I_N A~=A+IN为无向图G的带自环邻接矩阵
- I N I_N IN为单位矩阵
- D ~ i i = ∑ j A ~ i j \tilde{D}_{ii}=\sum_{j}\tilde{A}_{ij} D~ii=∑jA~ij
- W ( l ) W^{(l)} W(l)为layer-specific可训练权重向量
- σ ( ⋅ ) \sigma(·) σ(⋅)为激活函数,例:ReLU
- H ( l ) ∈ R N × D H^{(l)}\in\mathbb{R}^{N\times D} H(l)∈RN×D为第 l t h l^{th} lth层的激活矩阵; H ( 0 ) = X H^{(0)}=X H(0)=X
2.1 谱图卷积
推荐阅读:【GCN】图卷积网络初探——基于图(Graph)的傅里叶变换和卷积
在上面这篇文章中,我们推导出基于图的卷积公式如下:
( f ∗ h ) G = U ( h ^ ( λ 1 ) ⋱ h ^ ( λ n ) ) U T f (f*h)_G=U \begin{pmatrix} \hat{h}(\lambda_1) & & \\ & \ddots & \\ & & \hat{h}(\lambda_n) \end{pmatrix} U^T f (f∗h)G=U⎝⎛h^(λ1)⋱h^(λn)⎠⎞UTf
- f f f为待卷积函数(比如图的特征向量)
- h h h为按需设计的卷积核, h ^ \hat{h} h^为卷积核的傅里叶变换
- U U U为【图的拉普拉斯矩阵】的【特征向量矩阵】
- λ \lambda λ为图的拉普拉斯矩阵的特征值
之后,我们又提到了两种卷积核的设计:
第一代GCN:卷积核: d i a g ( h ^ ( λ l ) ) : d i a g ( θ l ) diag(\hat{h}(\lambda_l)): diag(\theta_l) diag(h^(λl)):diag(θl)
推导出的公式如下:
y o u t p u t = σ ( U ( θ 1 ⋱ θ n ) U T x ) y_{output}=\sigma \begin{pmatrix} U \begin{pmatrix} \theta_1 & & \\ & \ddots & \\ & & \theta_n \end{pmatrix} U^Tx \end{pmatrix} youtput=σ⎝⎛U⎝⎛θ1⋱θn⎠⎞UTx⎠⎞
第一代GCN的缺点为计算量大,因此提出第二代GCN如下
第二代GCN:卷积核: h ^ ( λ l ) : ∑ j = 0 K α j λ l j \hat{h}(\lambda_l):\sum_{j=0}^K \alpha_j\lambda_l^j h^(λl):∑j=0Kαjλlj
(经过矩阵变换后的)公式如下:
y o u t p u t = σ ( ∑ j = 0 K α j L j x ) y_{output}=\sigma \left( \sum_{j=0}^{K} \alpha_j L^j x \right) youtput=σ(j=0∑KαjLjx)
在这篇论文里,对上述引用中提到的这两种卷积核有着更为详细的解释。
第一种卷积
回到论文中,作者在2.1节的开头首先提出:考虑如下图卷积公式:
(2) g θ ∗ x = U g θ U T x g_{\theta}*x=Ug_{\theta}U^Tx \tag{2} gθ∗x=UgθUTx(2)
- x x x为图节点的特征向量
- g θ = d i a g ( θ ) g_{\theta}=diag(\theta) gθ=diag(θ)为卷积核,其中 θ \theta θ为参数
- U U U为图的拉普拉斯矩阵 L L L的特征向量矩阵
- 其中拉普拉斯矩阵 L = I N − D − 1 2 A D − 1 2 = U Λ U T L=I_N-D^{-\frac{1}{2}}AD^{-\frac{1}{2}}=U \Lambda U^T L=IN−D−21AD−21=UΛUT
可以看到,公式(2)就是上面引用中第一代GCN所使用的卷积公式,作者在论文中也提到,这个公式的缺点在于计算太过复杂,卷积核的选取不合适,需要改进。
改进:第二种卷积
作者接下来说,有人提出一种卷积核设计方法,即 g θ ( Λ ) g_{\theta}(\Lambda) gθ(Λ)可以用切比雪夫Chebyshev多项式 T k ( x ) T_k(x) Tk(x)到 K t h K^{th} Kth的截断展开来近似。
切比雪夫多项式:
(3) T k ( x ) = 2 x T k − 1 ( x ) − T k − 2 ( x ) T 0 ( x ) = 1 T 1 ( x ) = x \begin{aligned} &T_{k}(x)=2xT_{k-1}(x)-T_{k-2}(x) \tag{3}\\ &T_{0}(x)=1\\ &T_{1}(x)=x \end{aligned} Tk(x)=2xTk−1(x)−Tk−2(x)T0(x)=1T1(x)=x(3)
新的卷积核:
(4) g θ ‘ ( Λ ) ≈ ∑ k = 0 K θ k ′ T k ( Λ ~ ) g_{\theta‘}(\Lambda)\approx\sum_{k=0}^{K} \theta'_k T_k(\tilde{\Lambda}) \tag{4} gθ‘(Λ)≈k=0∑Kθk′Tk(Λ~)(4)
- Λ ~ = 2 Λ / λ m a x − I N \tilde{\Lambda}=2\Lambda/\lambda_{max}-I_N Λ~=2Λ/λmax−IN
- λ m a x \lambda_{max} λmax是 L L L的最大特征值
- θ ′ ∈ R K \theta'\in R_K θ′∈RK是切比雪夫系数的矢量
基于该卷积核,得到的卷积公式如下:
(5) g θ ‘ ∗ x = ∑ k = 0 K θ k ′ T k ( L ~ ) x g_{\theta‘}*x=\sum_{k=0}^{K} \theta'_k T_k(\tilde{L})x \tag{5} gθ‘∗x=k=0∑Kθk′Tk(L~)x(5)
- L ~ = 2 L / λ m a x − I N \tilde{L}=2L/\lambda_{max}-I_N L~=2L/λmax−IN
- 此公式为拉普拉斯算子中的 K t h K^{th} Kth-阶多项式,即它仅取决于离中央节点最大K步的节点。
可以看到,公式(4)与上面引文中的第二代GCN用到的卷积公式非常相似,最终都将参数简化到了 K K K个,并不再需要做特征分解,直接用拉普拉斯矩阵 L L L进行变换,计算复杂性大大降低。
但本文使用了切比雪夫多项式 T k ( x ) T_k(x) Tk(x),这是与上面引文中提到的第二代GCN中的卷积公式的不同点。
以上,都是前人的工作,都可以在本节开头的推荐阅读中找到详细推导和讲解。接下来是作者的改进部分。
2.2 线性模型
K=1:2个参数的模型
在2.1节中,我们定义了基于图的卷积公式(5)如下:
(5) g θ ′ ∗ x = ∑ k = 0 K θ k ′ T k ( L ~ ) x g_{\theta'}*x=\sum_{k=0}^{K} \theta'_k T_k(\tilde{L})x \tag{5} gθ′∗x=k=0∑Kθk′Tk(L~)x(5)
- L ~ = 2 L / λ m a x − I N \tilde{L}=2L/\lambda_{max}-I_N L~=2L/λmax−IN
现在我们可以通过堆叠多个形式为公式(5)的卷积层来建立一个GCN模型。
首先,我们将分层卷积操作限制为 K = 1 K=1 K=1,即关于 L L L是线性的,因此在拉普拉斯谱上有线性函数。
在GCN的这个线性公式中,我们进一步近似 λ m a x ≈ 2 \lambda_{max}\approx2 λmax≈2,我们可以预测到GCN的参数能够在训练中适应这一变化,此时公式(5)将简化为下式:
(6) g θ ′ ∗ x ≈ θ 0 ′ x + θ 1 ′ ( L − I N ) x = θ 0 ′ x − θ 1 ′ D − 1 2 A D − 1 2 x \begin{aligned} g_{\theta'}*x&\approx\theta'_{0}x+ \theta'_{1}(L-I_N)x\\ &=\theta'_{0}x- \theta'_{1}D^{-\frac{1}{2}}AD^{-\frac{1}{2}}x \tag{6} \end{aligned} gθ′∗x≈θ0′x+θ1′(L−IN)x=θ0′x−θ1′D−21AD−21x(6)
- 此公式具有两个自由参数: θ 0 ′ \theta'_{0} θ0′和 θ 1 ′ \theta'_{1} θ1′,滤波器参数将被整个图共享
- 连续应用这种形式的滤波器,可以有效的卷积节点的 k ( t h ) k^(th) k(th)-阶邻域,其中 k k k是模型中连续滤波操作或卷积层的数目。
简化:1个参数的模型
令 θ = θ 0 ′ = − θ 1 ′ \theta=\theta'_{0}=-\theta'_{1} θ=θ0′=−θ1′,将两个参数化为单参数 θ \theta θ,得到卷积公式如下:
(7) g θ ′ ∗ x ≈ θ ( I N + D − 1 2 A D − 1 2 ) x g_{\theta'}*x \approx \theta(I_N+D^{-\frac{1}{2}}AD^{-\frac{1}{2}})x \tag{7} gθ′∗x≈θ(IN+D−21AD−21)x(7)
注意 I N + D − 1 2 A D − 1 2 I_N+D^{-\frac{1}{2}}AD^{-\frac{1}{2}} IN+D−21AD−21拥有范围为 [ 0 , 2 ] [0,2] [0,2]的特征值,这将会导致数值不稳定性和梯度爆炸/消失。因此我们介绍下面的归一化技巧:
I N + D − 1 2 A D − 1 2 → D ~ − 1 2 A ~ D ~ − 1 2 I_N+D^{-\frac{1}{2}}AD^{-\frac{1}{2}} \to \tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}} IN+D−21AD−21→D~−21A~D~−21
- A ~ = A + I N \tilde{A}=A+I_N A~=A+IN
- D i i ~ = ∑ j A i j ~ \tilde{D_{ii}}=\sum_{j}\tilde{A_{ij}} Dii~=∑jAij~
推广:特征映射公式
将该定义推广到具有 C C C个输入通道(即每个节点的 C C C维特征向量)的信号 X ∈ R N × C X\in\mathbb{R^{N\times C}} X∈RN×C,和 F F F个滤波器,则特征映射(feature maps)如下:
(8) Z = D ~ − 1 2 A ~ D ~ − 1 2 X Θ Z=\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}X\Theta \tag{8} Z=D~−21A~D~−21XΘ(8)
- Θ ∈ R C × F \Theta\in\mathbb{R}^{C\times F} Θ∈RC×F是滤波器参数矩阵
- Z ∈ R N × F Z\in\mathbb{R}^{N\times F} Z∈RN×F是卷积后的信号矩阵
3 半监督节点分类
我们已经有了模型 f ( X , A ) f(X,A) f(X,A),可以在图上有效的传播信息,现在回到半监督节点分类问题上。
我们可以通过调整我们的模型 f ( X , A ) f(X,A) f(X,A),来放松通常在半监督学习中所做的假设。希望模型可以在【邻接矩阵 A A A中包含着(数据 X X X没有表达出来的)信息】这种情况下更有用。
一个整体的多层半监督GCN模型如下图所示:
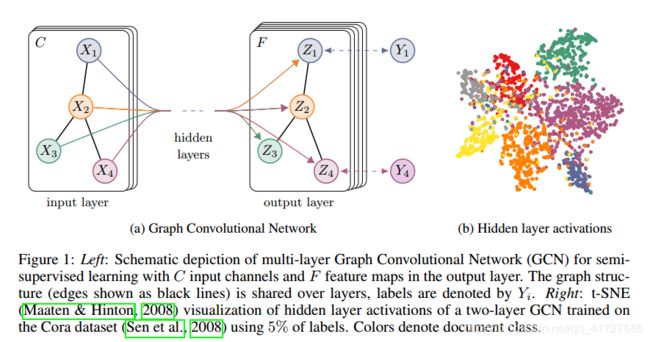
上图中,左(a)是一个GCN网络示意图,在输入层拥有 C C C个输入,中间有若干隐藏层,在输出层有 F F F个特征映射;图的结构(边用黑线表示)在层之间共享;标签用 Y i Y_{i} Yi表示。
右(b)是一个两层GCN在Cora数据集上(使用了5%的标签)训练得到的隐藏层激活值的形象化表示,颜色表示文档类别。
3.1 例子
考虑一个用于半监督图节点分类问题的两层GCN,邻接矩阵为 A A A(二进制/加权)。
预处理操作
在预处理操作中,计算 A ^ = D ~ − 1 2 A ~ D ~ − 1 2 \hat{A}=\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}} A^=D~−21A~D~−21,
这使得我们之前的模型更加简洁:
(9) Z = f ( X , A ) = s o f t m a x ( A ^ R e L U ( A ^ X W ( 0 ) ) W ( 1 ) ) Z=f(X,A)=softmax(\hat{A}\ ReLU(\hat{A}XW^{(0)})W^{(1)}) \tag{9} Z=f(X,A)=softmax(A^ ReLU(A^XW(0))W(1))(9)
- W ( 0 ) ∈ R C × H W^{(0)}\in\mathbb{R}^{C\times H} W(0)∈RC×H为输入层-到-隐藏层的权重矩阵,该隐藏层具有 H H H个特征映射
- W ( 1 ) ∈ R H × F W^{(1)}\in\mathbb{R}^{H\times F} W(1)∈RH×F为隐藏层-到-输出层的权重矩阵
- softmax激活函数: s o f t m a x ( x i ) = 1 ∑ i e x p ( x i ) e x p ( x i ) softmax(x_i)=\frac{1}{\sum_i exp(x_i)} exp(x_i) softmax(xi)=∑iexp(xi)1exp(xi),作用在每一行上
交叉熵误差
接下来,对于半监督多类别分类,我们评估所有标记标签的交叉熵误差:
(10) L = − ∑ l ∈ Y L ∑ f = 1 F Y l f l n Z l f \mathcal{L}=-\sum_{l\in\mathcal{Y}_L}\sum_{f=1}^{F}Y_{lf}lnZ_{lf}\tag{10} L=−l∈YL∑f=1∑FYlflnZlf(10)
- Y L \mathcal{Y}_L YL为带标签的节点集
训练
网络中的权重 W ( 0 ) W^{(0)} W(0)和 W ( 1 ) W^{(1)} W(1)通过梯度下降训练。
我们对每个【训练迭代】使用完整的数据集执行【批量梯度下降】,这是一个可行的选择,只要数据集适合内存。
对于 A A A使用稀疏表示,即边数是线性的。
通过Dropout引入训练过程中的随机性。
我们将内存效率扩展与小批随机梯度下降留作以后的工作。
3.2 实现
利用TensorFlow,基于GPU的【稀疏-密集矩阵乘法】高效实现公式(9):
(9) Z = f ( X , A ) = s o f t m a x ( A ^ R e L U ( A ^ X W ( 0 ) ) W ( 1 ) ) Z=f(X,A)=softmax(\hat{A}\ ReLU(\hat{A}XW^{(0)})W^{(1)}) \tag{9} Z=f(X,A)=softmax(A^ ReLU(A^XW(0))W(1))(9)
5 实验
- 引文网络:半监督文档分类
- 从知识图中提取的二分图:半监督实体分类
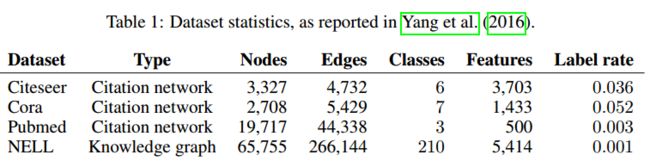
5.1 数据集
5.2 实验参数
- 使用3.1节中的两层GCN网络
- prediction accuracy:1000张带标签测试集
- 对比实验:十层网络
- 使用500张带标签验证集:超参数的初始化
- 所有层的dropout率
- 第一层的L2正则化因子
- 隐藏层单元的个数
1、引文网络数据集
- 最大200迭代期
- Adam算法
- 学习率为0.01
- 停止条件:验证集loss连续十个迭代期没有下降
- 权重初始化方法:Xavier Glorot and Yoshua Bengio. Understanding the difficulty of training deep feedforward neural networks. In AISTATS, volume 9, pp. 249–256, 2010.
- (按行)对输入特征向量归一化
2、随机图数据集
- 隐藏层32个单元
- 省略dropout和L2正则化
6 结果
6.1 半监督节点分类
【参考博文】
1、semi_supervised classification with graph convolutional networks论文阅读报告(1)
2、SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS个人理解
3、翻译–SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS